Chapter 10 Basics of Confidence Intervals September 21

Chapter 10: Basics of Confidence Intervals September 21 10: Intro to Confidence Intervals 1

In Chapter 10: 10. 1 Introduction to Estimation 10. 2 Confidence Interval for μ (σ known) 10. 3 Sample Size Requirements 10. 4 Relationship Between Hypothesis Testing and Confidence Intervals 9/25/2021 2

Statistical Inference Recall the goal of statistical inference: We want to learn about population parameters … 9/25/2021 using statistics calculated in the sample 3

Recall: • The distinction between a sample statistic (e. g. , sample mean “x-bar”) and population parameter (e. g. , population mean µ) • The two forms of statistical inference: – Hypothesis testing (Introduced in Ch 9) – Estimation (Introduced in this chapter) We introduce estimation concepts with the one-sample z CI for µ 9/25/2021 4

Estimating µ, σ known Objective: to estimate the value of population mean µ under these conditions • Simple Random Sample (SRS) • Population Normal or large sample • The value of σ is known • The value of μ is NOT known 9/25/2021 5

Estimating µ Two forms of estimation • Point estimation ≡ most likely value of parameter µ (i. e. , sample mean x-bar) • Interval estimate ≡ the sample mean is surrounded with a margin of error to create a confidence interval (CI) 9/25/2021 6

(1 – α)100% Level of Confidence (1 – α)100% 9/25/2021 7

Common Levels of Confidence level 1–α. 90 Alpha level α. 10 Z value z 1–(α/2) 1. 645 . 95 . 05 1. 960 . 99 . 01 2. 576 9/25/2021 8

(1 – α)100% CI for µ margin of error m where: 9/25/2021 9

95% CI for µ (Example) • Body weights of 20 -29 -year-old males • Unknown μ, σ = 40 • SRS of n = 64 calculate x-bar =183 margin of error m We have 95% confidence µ is in this interval 9/25/2021 10

99% CI for µ (Example) • Body weights of 20 -29 -year-old males • Unknown μ, σ = 40 • SRS of n = 64 sample mean x-bar =183 margin of error m We have 99% confidence µ is in this interval 9/25/2021 11

How 95% CIs behave 9/25/2021 12

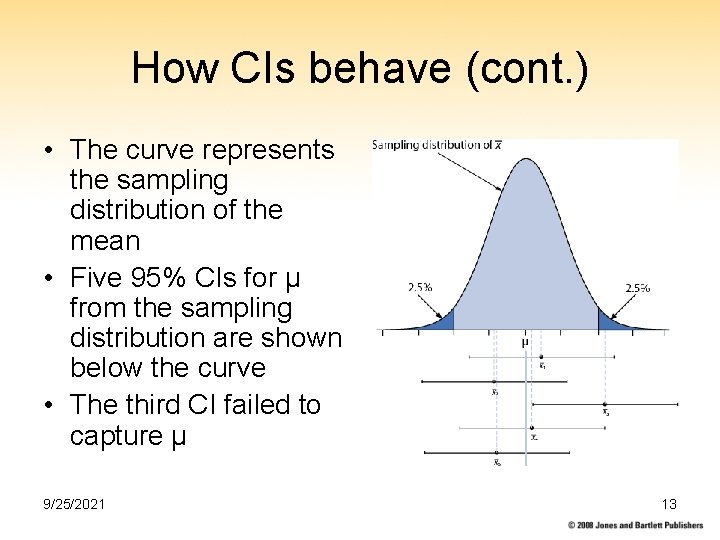
How CIs behave (cont. ) • The curve represents the sampling distribution of the mean • Five 95% CIs for µ from the sampling distribution are shown below the curve • The third CI failed to capture μ 9/25/2021 13

Sample Size Requirements How large a sample is need for a (1 – α)100% CI for µ with margin of error m? Examples (next slide) use these assumptions: • σ = 40 • 95% confidence z 1–. 05/2 = z. 975 = 1. 96 • Varying m 9/25/2021 14

Examples: Sample Size Requirements Round-up to next integer so m no greater than stated 1. Smaller m requires larger n Square root law: quadruple n to double precision 9/25/2021 15

10. 4 Relation Between Testing and Confidence Intervals Rule: Reject H 0 at the α level for significance when μ 0 falls outside the (1−α)100% CI. Illustrations: Next slide 9/25/2021 16

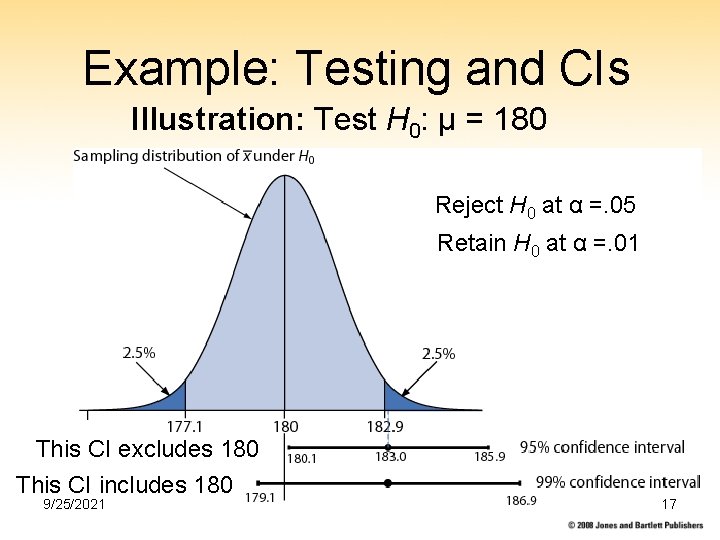
Example: Testing and CIs Illustration: Test H 0: μ = 180 Reject H 0 at α =. 05 Retain H 0 at α =. 01 This CI excludes 180 This CI includes 180 9/25/2021 17