Chapter 10 An Effective Technique for Mixedinteger Optimization

Chapter 10 An Effective Technique for Mixed-integer Optimization

Outline o Sequential fixing: An introduction o Case study n Spectrum sharing in cognitive radio networks 2

Basic Idea o Since a MINLP problem is NP-hard in general, we aim to obtain a near-optimal solution o Branch-and-bound framework can guarantee (1 -e)-optimal solution to MINLP, but its worst case complexity is exponential o A heuristic algorithm: Sequential fixing n Competitive solution for certain MINLP and any MILP o Problem is reduced to LP once we know the values of all integer variables n Iteratively determine integer variables n Determine other variables via LP 3

Determine all Integer Variables o The performance of the solution depends on the values of integer variables n If we can obtain the optimal values of integer variables, the obtained solution is optimal o Key challenge: How to determine the integer variables? o Approach: n Solve the linear relaxation of the problem n Fix one or more integer variables based on the solution to the LP-relaxed problem n Repeat the above steps until all integer variables are fixed 4

SF Framework o Relax all integer variables and solve the relaxed LP step 2 o Fix the variable whose value is closest to integer o If some integer variables are unfixed, reformulate and solve a newly relaxed LP with the newly fixed variables, go step 2 o Otherwise, formulate and solve the LP based on all fixed variables. Done! Polynomial time complexity! 5

Performance Analysis (for a minimization problem) o Develop a lower bound o Compare the obtained solution with the lower bound o If the obtained solution is close to the lower bound, then n The lower bound is tight n The obtained solution is even closer to the optimum 6

Outline o Sequential fixing: An introduction o Case study n Spectrum sharing in cognitive radio networks 7

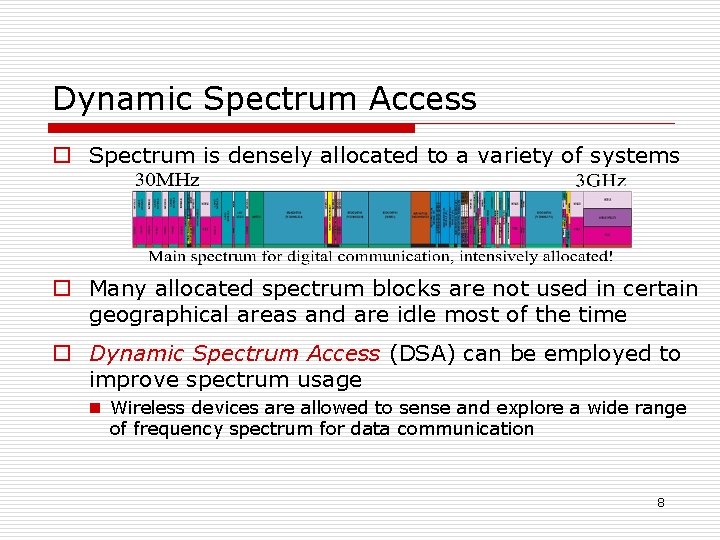
Dynamic Spectrum Access o Spectrum is densely allocated to a variety of systems o Many allocated spectrum blocks are not used in certain geographical areas and are idle most of the time o Dynamic Spectrum Access (DSA) can be employed to improve spectrum usage n Wireless devices are allowed to sense and explore a wide range of frequency spectrum for data communication 8

Cognitive Radio o Each node can sense available spectrum n Each node may have a different set of available spectrum (or channels) n Each frequency band is likely to have different bandwidth o Each node can transmit over non-contiguous frequency bands n Radio may switch frequency bands on a per-packet basis 9

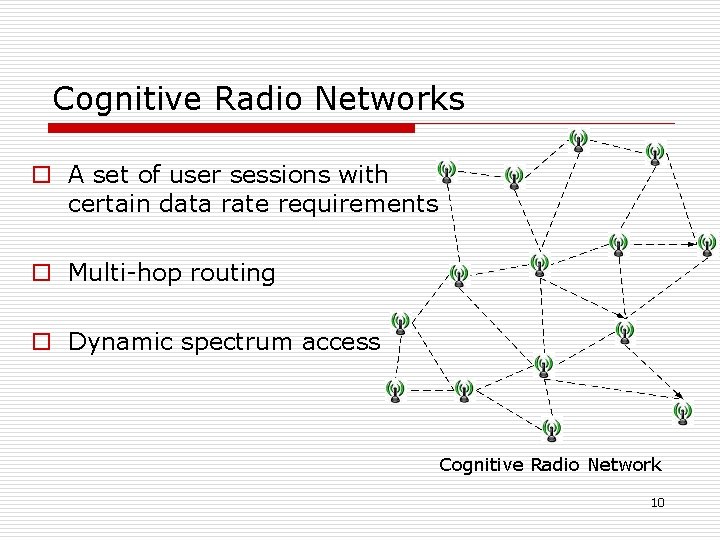
Cognitive Radio Networks o A set of user sessions with certain data rate requirements o Multi-hop routing o Dynamic spectrum access Cognitive Radio Network 10

Outline of Case Study o Problem statement and formulation o Find a lower bound o A near-optimal solution based on SF o Numerical Examples 11

Problem Statement o Problem Setting: n Multi-hop cognitive radio network n Available frequency bands at each node may be different; each frequency band may be of different size n A set of communication sessions, each with a data rate requirement o Objective: Minimize the total used spectrum resource o Question: How to perform spectrum allocation, scheduling, and routing? 12

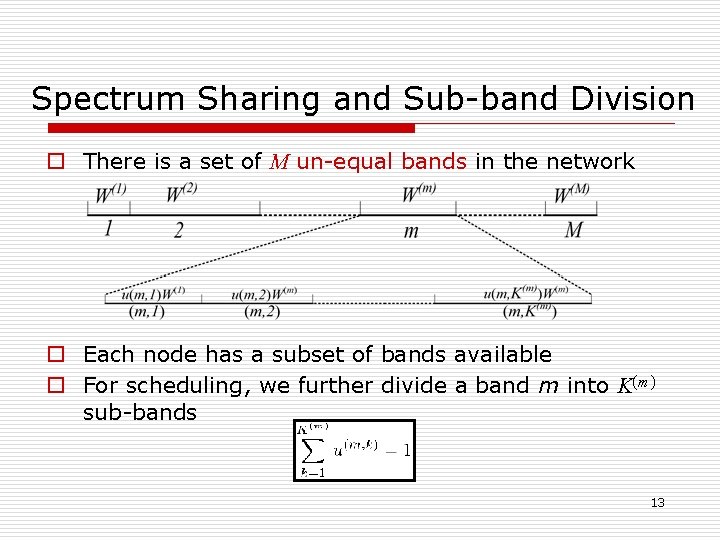
Spectrum Sharing and Sub-band Division o There is a set of M un-equal bands in the network o Each node has a subset of bands available o For scheduling, we further divide a band m into K(m) sub-bands 13

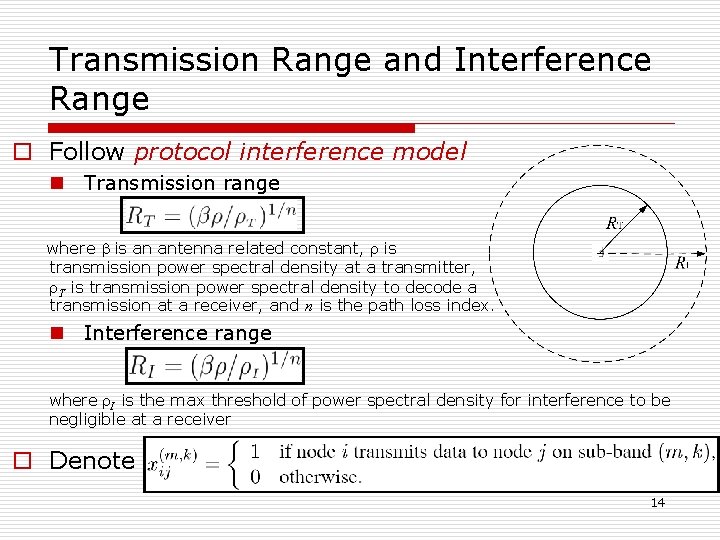
Transmission Range and Interference Range o Follow protocol interference model n Transmission range where b is an antenna related constant, r is transmission power spectral density at a transmitter, r. T is transmission power spectral density to decode a transmission at a receiver, and n is the path loss index. n Interference range where r. I is the max threshold of power spectral density for interference to be negligible at a receiver o Denote 14

Scheduling and Interference Constraints o A node i cannot transmit to multiple nodes on the same sub-band o A receiving node j cannot be in the interference range of any other transmitting nodes on the same sub-band 15

Flow Routing o For each session, allow flow splitting for maximum flexibility (and optimality) o Flow balance constraints for session l: n If node i is the source node, then n If node i is the destination node, then redundancy n For all other nodes, we have 16

Link Capacity Constraint o Capacity on link i j on sub-band (m, k) o Aggregate flow on link i j cannot exceed link capacity 17

Problem Formulation Transmission constraint Band division constraint non-linear Interference constraint Link capacity constraint Flow balance constraint integer A mixed-integer non-linear program (MINLP) 18

Outline of Case Study o Problem formulation o Find a lower bound o A near optimal solution based on SF o Numerical Examples 19

Linear Relaxation o A lower bound can be found via linear relaxation to the MINLP problem n Relax integer variables: integer continuous n Remove nonlinear terms: let 20

Relaxed LP constant continuous This problem can be solved in polynomial time. 21

Outline of Case Study o Problem formulation o Find a lower bound o A near-optimal solution based on SF o Numerical Examples 22

Main Idea o Determine all x-variables iteratively via a series of LPs n If in the relaxed problem formulation is close to 1, then sub-band (m, k) may be used for transmission on link i j n Therefore, set o At each iteration, one or more x-variables can be fixed o Once all x-variables are fixed, the routing problem can be solved via a single LP 23

Algorithm Details o Set up a LP problem by relaxing its binary variables to , and solve it step 2 o Fix the largest x-variable to 1 o If some x-variables are unfixed, reformulate and solve a newly relaxed LP with the newly fixed -variables, go step 2 x o Otherwise, formulate and solve the LP based on all fixed x-values. Done! 24

An Iteration-Speedup Technique o To further decrease the complexity, we can fix more x-variables during each iteration n Choose a threshold a, and fix all x-variables greater than a to 1 o Justification of this approach n Fixing multiple x-variables to 1 means that multiple links can be active simultaneously n From the space perspective, two links far from each other will not interfere each other n From the frequency perspective, no interference exists between two links if they use different sub-bands 25

Outline of Case Study o Problem Formulation o Find A Lower Bound o A Near Optimal Solution Based on SF o Numerical Examples 26

Simulation Setting o 20, 30, and 40 nodes in a 500 x 500 area o 5 active sessions with a rate in [10, 100] Mbps o Each band can be further divided for scheduling o Transmission range is 100 m; interference range is 150 m o Other parameters 27

Results for 20 -node Network Normalized Results: Results from SF algorithm / a lower bound Average 1. 04 Standard derivation: 0. 07 The simulation results demonstrate: o The solution from SF, the optimal solution, and the lower bound are the same! The solution obtained by SF is optimal o o The solution is close to the lower bound The solution is even closer to the optimum The lower bound is very tight 28

Results for The First 40 Data Sets 29

Results for 30&40 -node Network 30 -node network Normalized results: l Average 1. 10 l Standard derivation 0. 16 40 -node network Normalized results: l Average 1. 18 30 l Standard derivation 0. 16

Summary o Introduced the SF technique for mixed integer optimization o Investigated spectrum allocation, scheduling, and routing problem for CRN o Formulated a cross-layer optimization problem o Developed a near-optimal algorithm via SF technique n Near optimality was substantiated by comparing a lower bound n The complexity of the algorithm is polynomial time 31