Chapter 10 Addition of Angular Momenta Total angular

Chapter 10 Addition of Angular Momenta

Total angular momentum 10. A. 1 10. A. 2 • Let us recall the definition of the classical angular momentum of a system of particles: • What is the quantum equivalent of the total angular momentum of the system in which there are parts with their own angular momenta? • The answer: • What are the eigenvalues and the eigenstates associated with this observable?

Addition of two spin-½’s 10. B. 1 • Let us start with the simplest nontrivial case of two angular momenta being added, each of spin ½: • The state space is 4 D: • The orthonormal basis: • These are the eigenstates of this set of operators: • It comprises a CSCO

Addition of two spin-½’s • The eigneproblem: • S is also an angular momentum operator: • Similarly: • So: 10. B. 1

Addition of two spin-½’s • Another important operator is: 10. B. 1

Addition of two spin-½’s • Another important operator is: 10. B. 1

Addition of two spin-½’s • Important commutation relations: • What about this commutator? 10. B. 1

Addition of two spin-½’s • Let us calculate: • Since 10. B. 1

Basis change 10. B. 1 • We just showed that these observables commute: • Since • This set is not the same as the CSCO • Is this a CSCO? : • In other words, is there a new basis that will satisfy these equations?

Basis change • Since • One can write: • Thus: • I. e. , 10. B. 2

Basis change • So: 10. B. 2

Basis change • Let us recall: • Then: 10. B. 3

Basis change • Let us recall: • Then: 10. B. 3

Basis change • Let us recall: • Then: 10. B. 3

Basis change • Let us recall: • Then: 10. B. 3

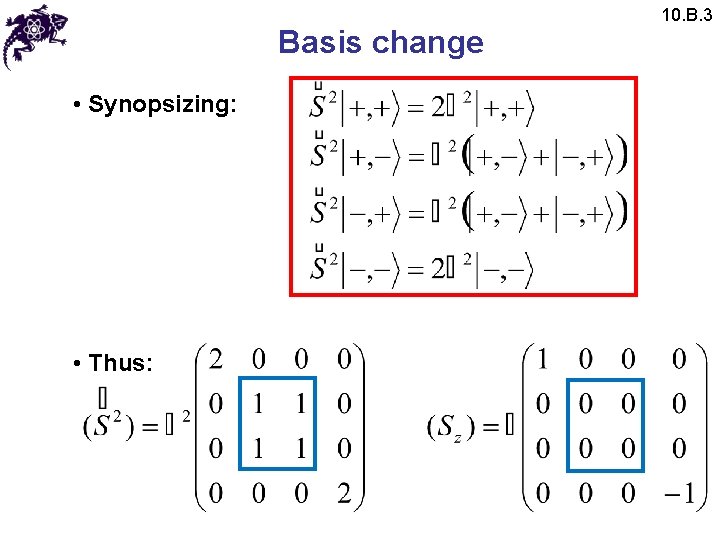
Basis change • Synopsizing: • Thus: 10. B. 3

Basis change • Let us diagonalize this matrix: • Secular equation: • Roots: + - 10. B. 3

Basis change • Normalizing: 10. B. 3

Basis change • Thus, we found all four eigenstates: • The corresponding values of M: • Thus the corresponding values of S: 10. B. 3

Basis change 10. B. 4 • So, we successfully obtained the new orthonormal basis: • The first three states with S = 1 are called a triplet, and the fourth state with S = 0 is called a singlet

Basis change 10. B. 4 • So, we successfully obtained the new orthonormal basis: • As a result of the basis change the subspace allocation became different:

Basis change 10. C. 4 • The same results can be obtained using the ladder operators • Recall:

Basis change 10. C. 4 • The same results can be obtained using the ladder operators • Recall:

Basis change • On the other hand • Similarly: 10. C. 4

10. C. 2 Case of two arbitrary angular momenta • Let us consider addition of two angular momenta:

10. C. 2 Case of two arbitrary angular momenta • The state space is: • Each subspace in the tensor sum has a dimension of (2 j 1 + 1)·(2 j 2 + 1)

10. C. 2 Case of two arbitrary angular momenta • J is also an angular momentum operator: • Similarly: • So: • Moreover:

10. C. 2 Case of two arbitrary angular momenta • Important commutation relations:

Basis change 10. C. 2 • The eigneproblem: • We just showed that these observables commute: • Since • This set is not the same as: • Is there a new state set satisfying these equations?

Basis change 10. C. 2 • If this is the case, the following tensor sum can be considered: • The following questions have to be answered: • 1) What are the values of J for a given pair of j 1 and j 2? • 2) How can the eigenvectors of J 2 and Jz be expanded via the basis of eigenvectors of Ji 2 and Jiz?

Eigenvalues of J 2 and Jz • Let us assume that • Thus • Since • One can write • What is the degeneracy of these values? 10. C. 3

Eigenvalues of J 2 and Jz • Consider a case 10. C. 3

Eigenvalues of J 2 and Jz • Consider a case 10. C. 3

Eigenvalues of J 2 and Jz • Consider a case 10. C. 3

Eigenvalues of J 2 and Jz • Consider a case 10. C. 3

Eigenvalues of J 2 and Jz • Consider a case 10. C. 3

Eigenvalues of J 2 and Jz • The following dependence is obvious: 10. C. 3

Eigenvalues of J 2 and Jz • The following dependence is obvious: 10. C. 3

Eigenvalues of J 2 and Jz • The following dependence is obvious: 10. C. 3

Eigenvalues of J 2 and Jz 10. C. 3 • Thus, for given j 1 and j 2, the eigenvalues of J 2 are: • One can associate a single invariant subspace E (J) with each of these values • For each value of J and each value of M, compatible with it, there is only one state vector in E (j 1, j 2) • Therefore, J 2 and Jz comprise a CSCO in E (j 1, j 2)

Eigenstates of J 2 and Jz • As a result: • Let us start with the first subspace E (j 1 + j 2) • Setting: • Application of the lowering operator should yield: 10. C. 4

Eigenstates of J 2 and Jz 10. C. 4

Eigenstates of J 2 and Jz 10. C. 4

Eigenstates of J 2 and Jz 10. C. 4 • This procedure can be repeated by further applying the lowering ladder operator until reaching • The same approach can be used for • Here, the new maximum value of M is: • The corresponding eigenvector should be proportional to

Eigenstates of J 2 and Jz • Assuming • With • It should be orthogonal to: • Thus: • Solution: 10. C. 4

Eigenstates of J 2 and Jz 10. C. 4 • Thereby: • The rest of the states can be obtained by a repeated application of the lowering ladder operator until reaching • Then, the tensor sum is considered: • Etc.

Clebsch-Gordan coefficients 10. C. 4 • Recall that inside a given space E (j 1, j 2) this set is a basis: • It is complete, thus the closure relation applies: • Using it we can write down the following expansion:

Clebsch-Gordan coefficients • These coefficients are called Clebsch-Gordan coefficients Rudolf Friedrich Alfred Clebsch (1833 – 1872) Paul Albert Gordan (1837 – 1912) 10. C. 4

Clebsch-Gordan coefficients 10. C. 4 • Conventionally, the Clebsch-Gordan coefficients are chosen to be real • On the other hand, since this set is a complete basis: • The closure relation applies: • Thus:

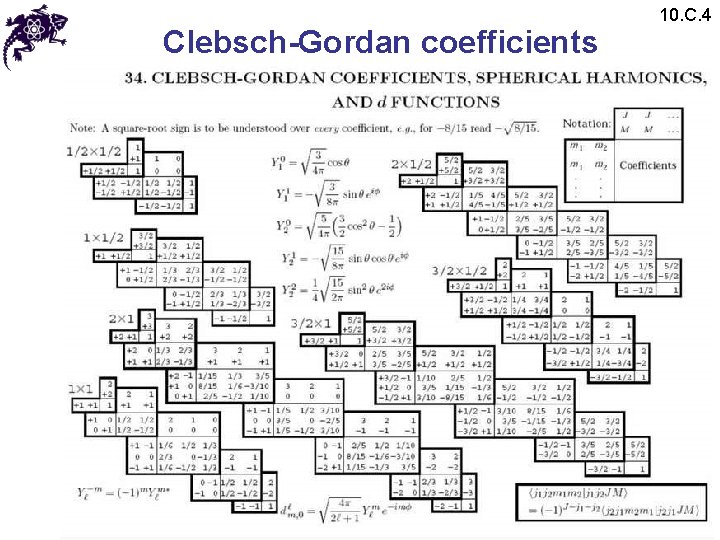
Clebsch-Gordan coefficients 10. C. 4 • The Clebsch-Gordan coefficients can be calculated by iteration using the ladder operators • Usually they are compiled in a tabular form:

Clebsch-Gordan coefficients 10. C. 4