Chapter 10 3 and 10 4 Combinatorial Circuits

Chapter 10. 3 and 10. 4: Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications

Learning Objectives q Explore the application of Boolean algebra in the design of electronic circuits q Learn the application of Boolean algebra in switching circuits Discrete Mathematical Structures: Theory and Applications 2

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 3

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 4

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 5

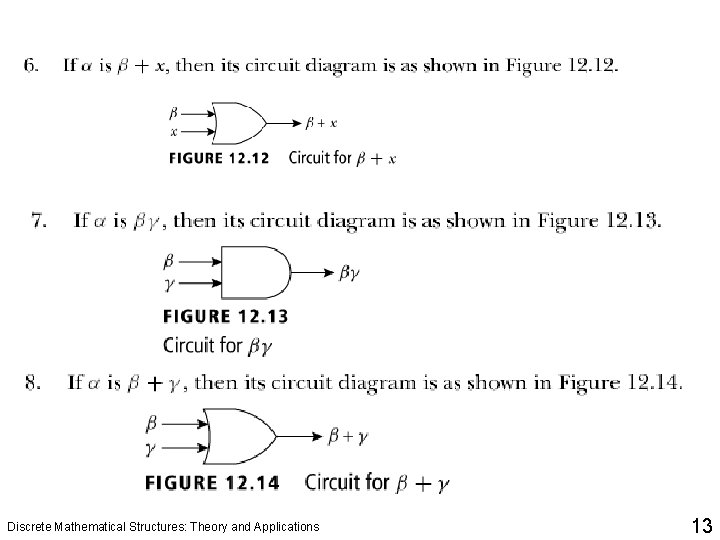
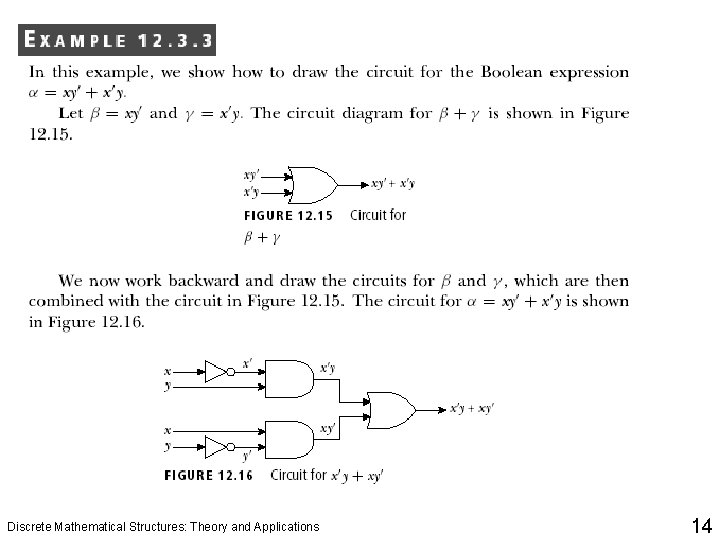
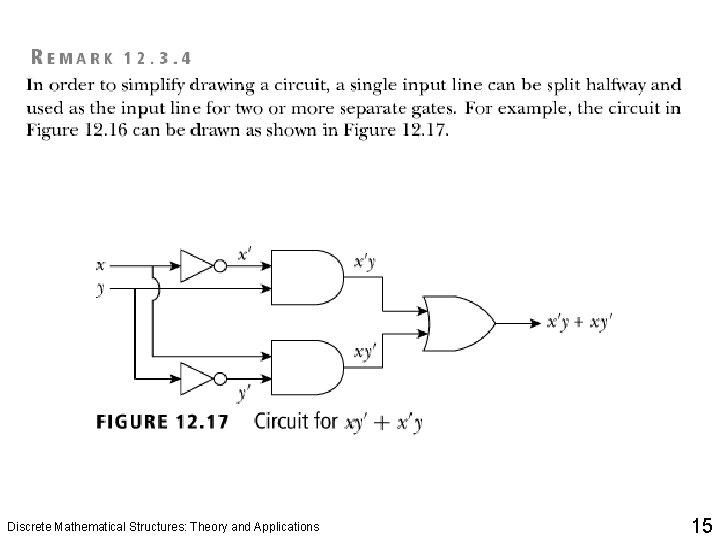
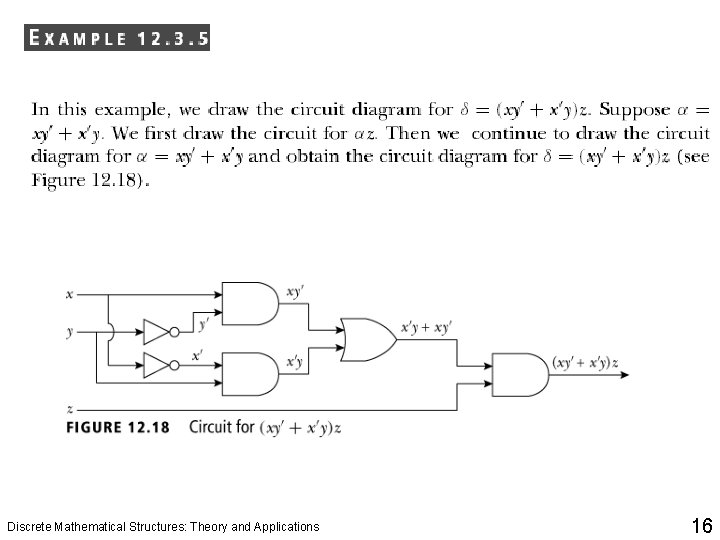
Logical Gates and Combinatorial Circuits q In circuitry theory, NOT, AND, and OR gates are the basic gates. Any circuit can be designed using these gates. The circuits designed depend only on the inputs, not on the output. In other words, these circuits have no memory. Also these circuits are called combinatorial circuits. q The symbols NOT gate, AND gate, and OR gate are also considered as basic circuit symbols, which are used to build general circuits. The word circuit instead of symbol is also used. Discrete Mathematical Structures: Theory and Applications 6

Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications 7

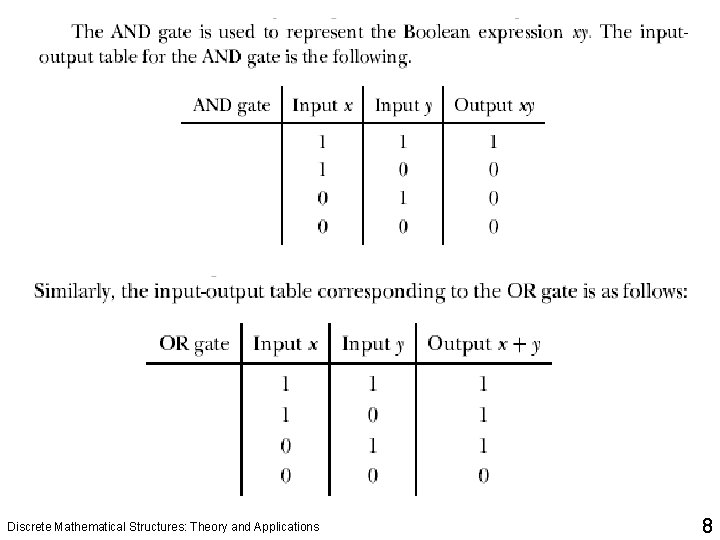
Discrete Mathematical Structures: Theory and Applications 8

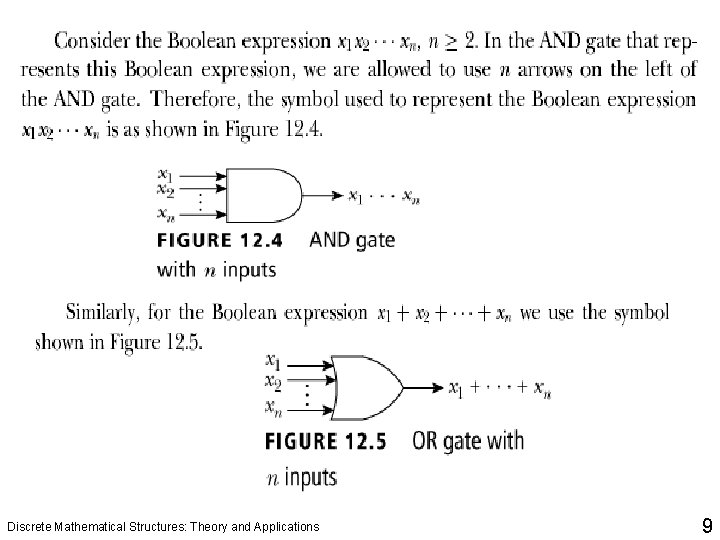
Discrete Mathematical Structures: Theory and Applications 9

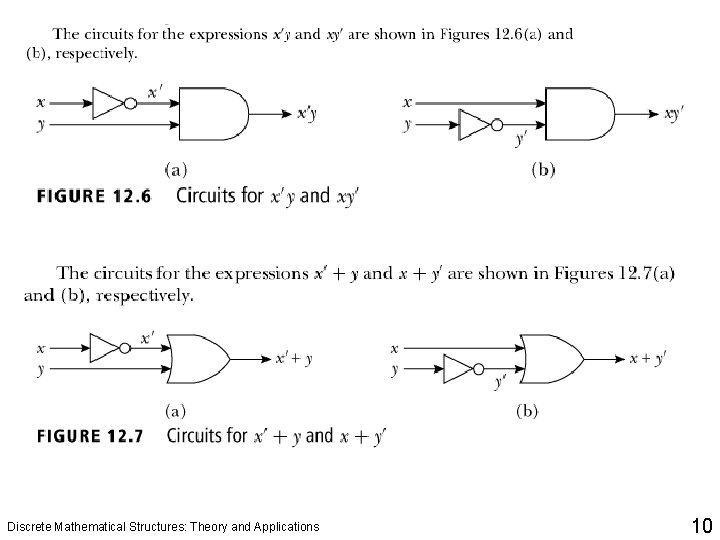
Discrete Mathematical Structures: Theory and Applications 10

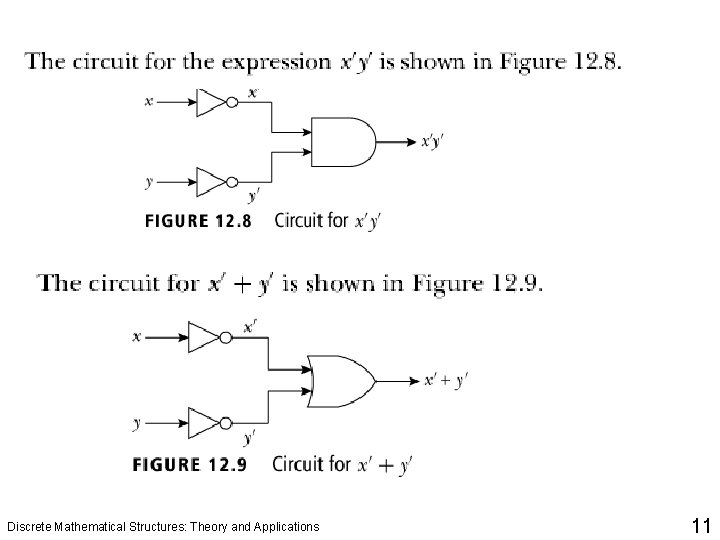
Discrete Mathematical Structures: Theory and Applications 11

Discrete Mathematical Structures: Theory and Applications 12

Discrete Mathematical Structures: Theory and Applications 13

Discrete Mathematical Structures: Theory and Applications 14

Discrete Mathematical Structures: Theory and Applications 15

Discrete Mathematical Structures: Theory and Applications 16

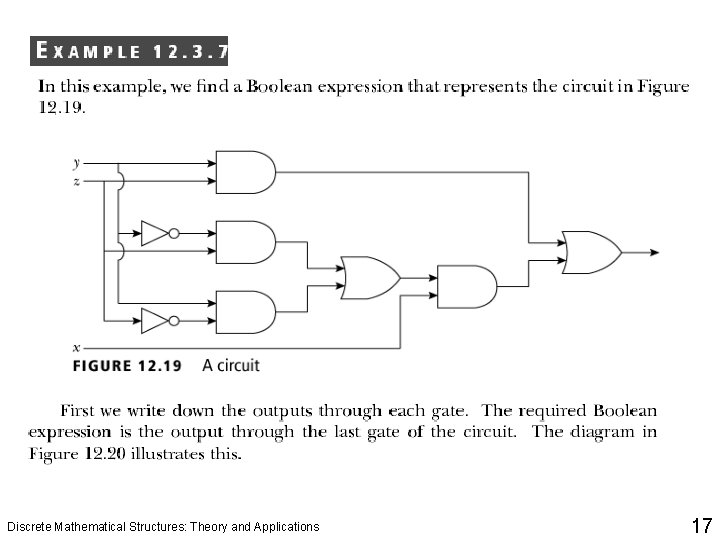
Discrete Mathematical Structures: Theory and Applications 17

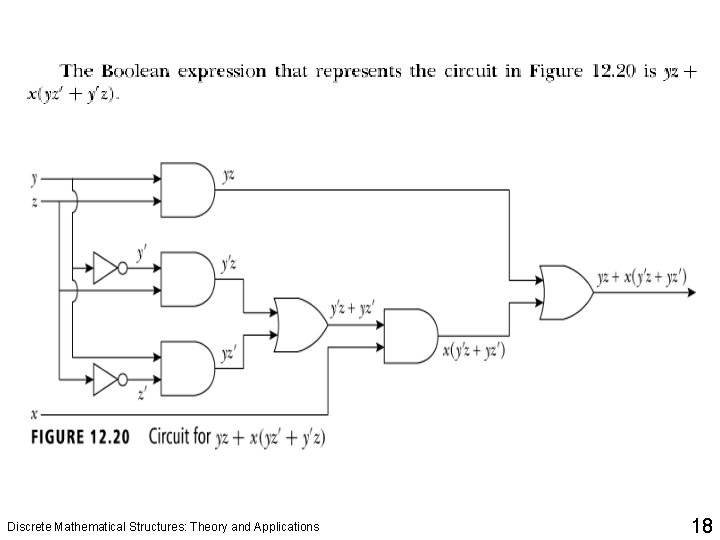
Discrete Mathematical Structures: Theory and Applications 18

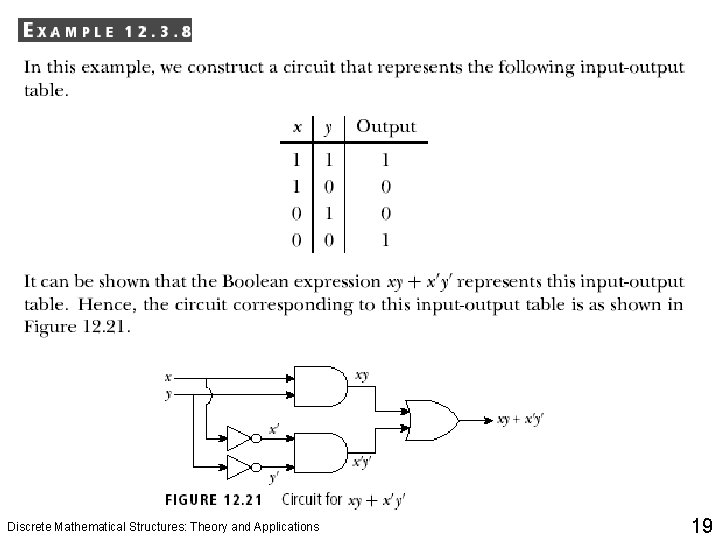
Discrete Mathematical Structures: Theory and Applications 19

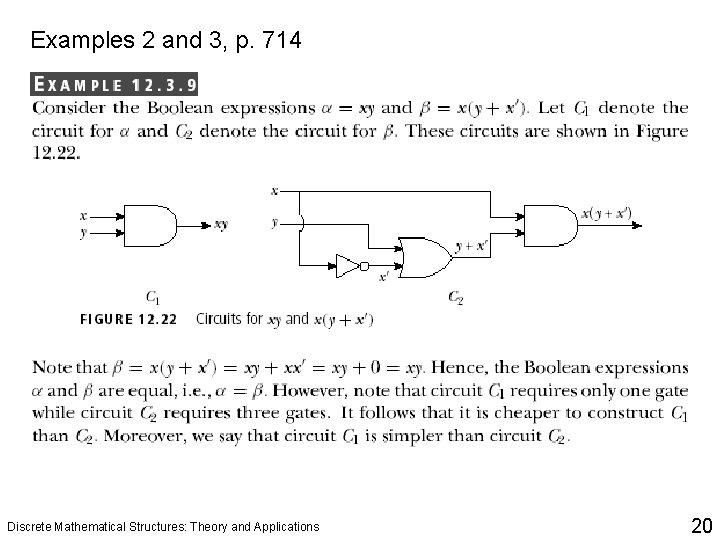
Examples 2 and 3, p. 714 Discrete Mathematical Structures: Theory and Applications 20

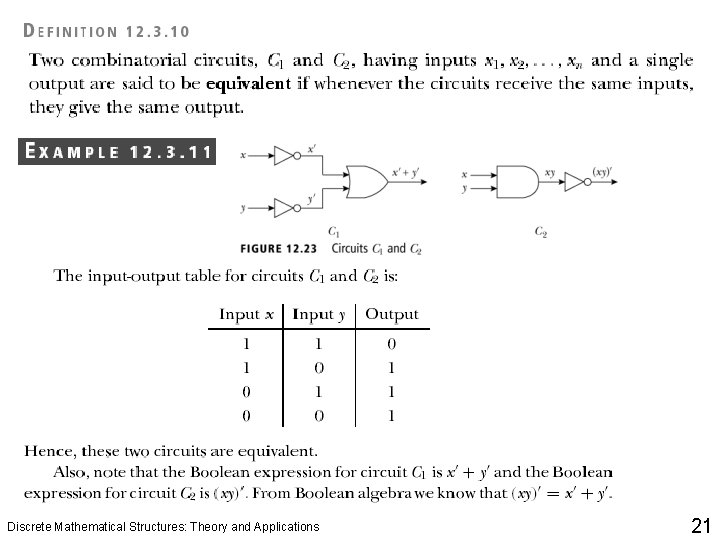
Discrete Mathematical Structures: Theory and Applications 21

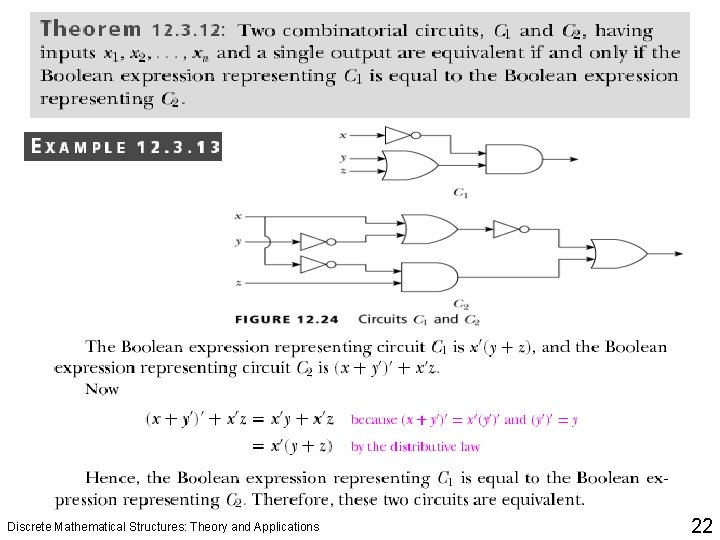
Discrete Mathematical Structures: Theory and Applications 22

Discrete Mathematical Structures: Theory and Applications 23

Discrete Mathematical Structures: Theory and Applications 24

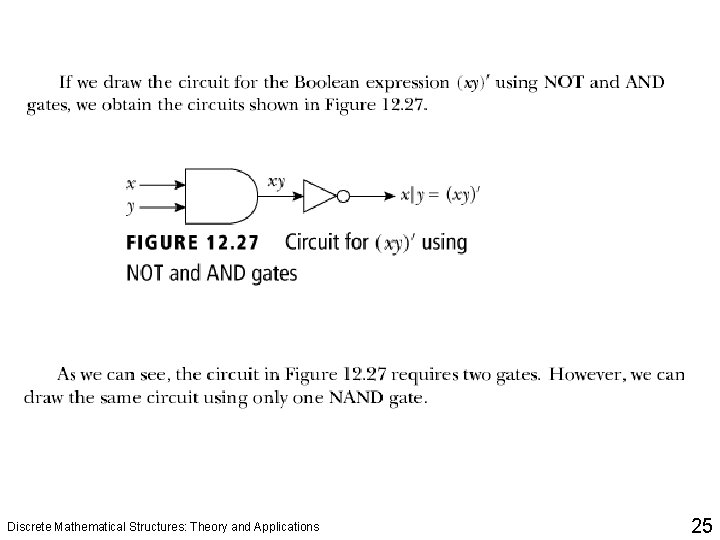
Discrete Mathematical Structures: Theory and Applications 25

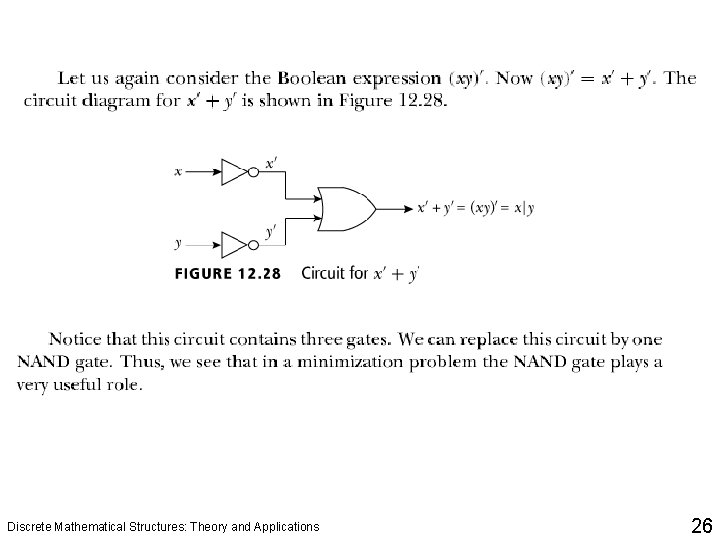
Discrete Mathematical Structures: Theory and Applications 26

Discrete Mathematical Structures: Theory and Applications 27

Discrete Mathematical Structures: Theory and Applications 28

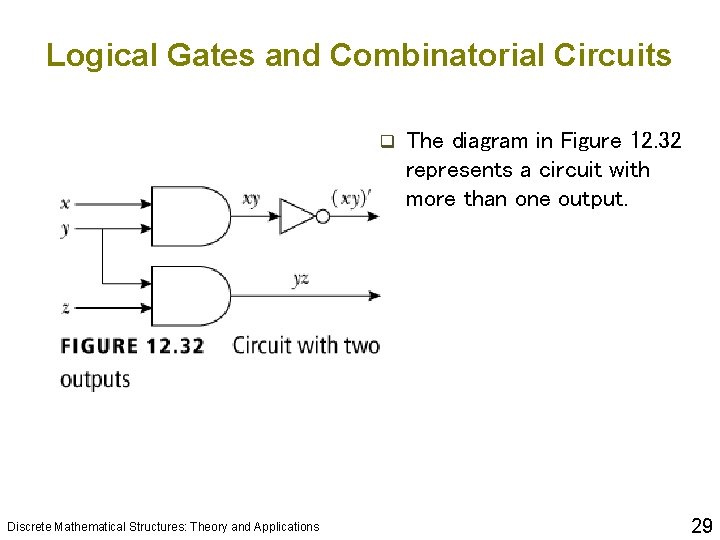
Logical Gates and Combinatorial Circuits q Discrete Mathematical Structures: Theory and Applications The diagram in Figure 12. 32 represents a circuit with more than one output. 29

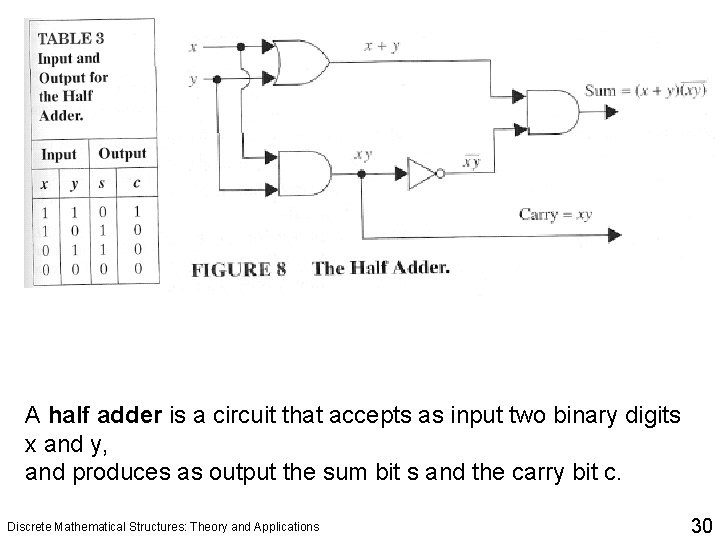
A half adder is a circuit that accepts as input two binary digits x and y, and produces as output the sum bit s and the carry bit c. Discrete Mathematical Structures: Theory and Applications 30

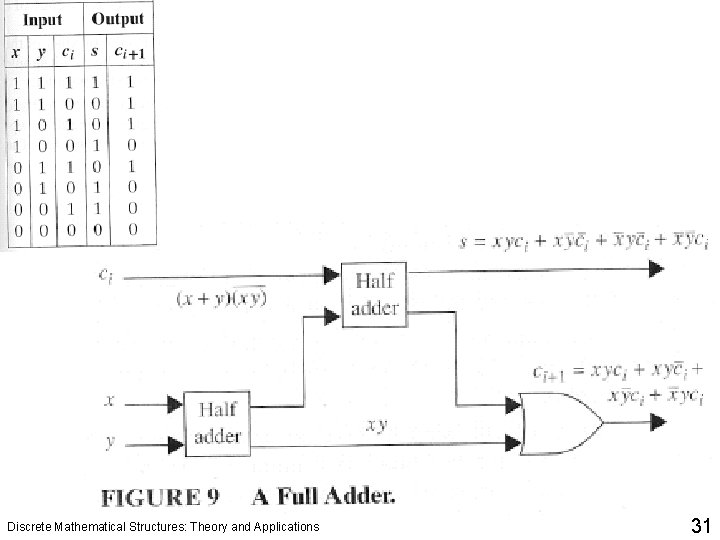
Discrete Mathematical Structures: Theory and Applications 31

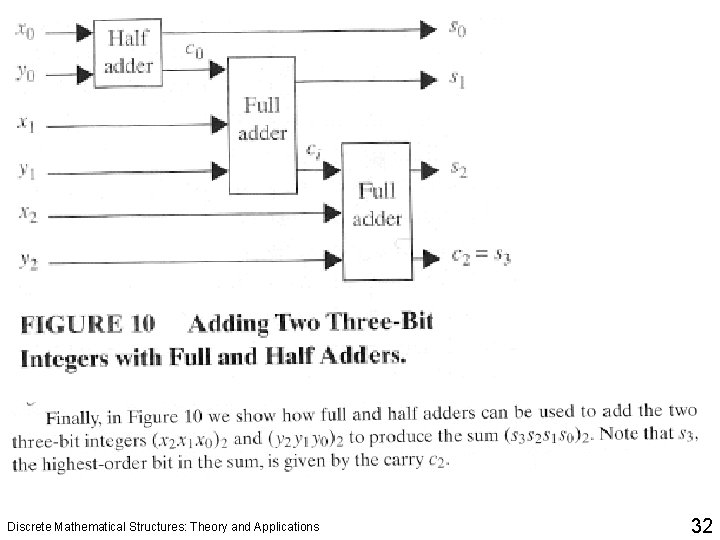
Discrete Mathematical Structures: Theory and Applications 32

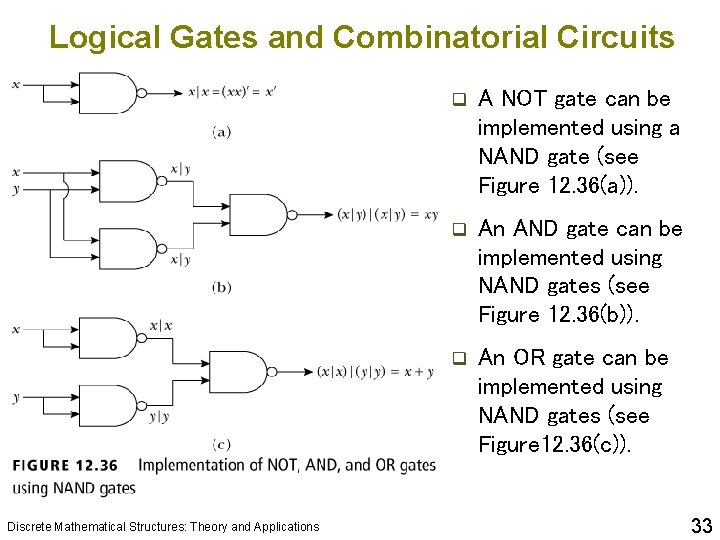
Logical Gates and Combinatorial Circuits Discrete Mathematical Structures: Theory and Applications q A NOT gate can be implemented using a NAND gate (see Figure 12. 36(a)). q An AND gate can be implemented using NAND gates (see Figure 12. 36(b)). q An OR gate can be implemented using NAND gates (see Figure 12. 36(c)). 33

Logical Gates and Combinatorial Circuits q Any circuit which is designed by using NOT, AND, and OR gates can also be designed using only NAND gates. q Any circuit which is designed by using NOT, AND, and OR gates can also be designed using only NOR gates. Discrete Mathematical Structures: Theory and Applications 34

Discrete Mathematical Structures: Theory and Applications 35

Discrete Mathematical Structures: Theory and Applications 36

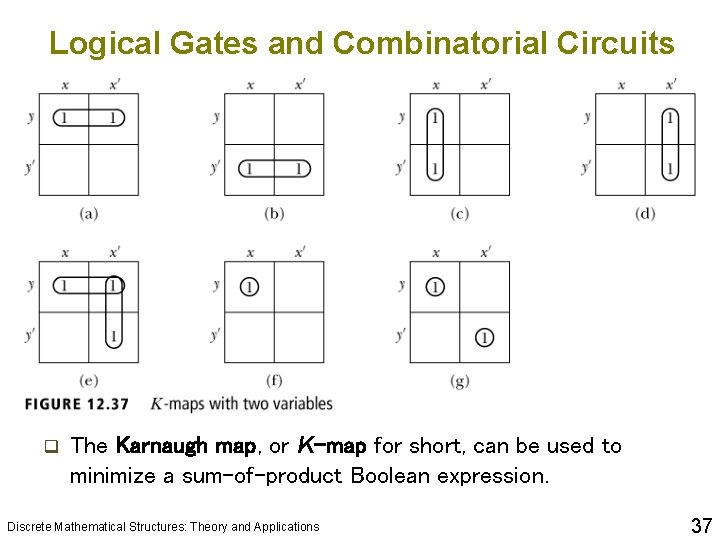
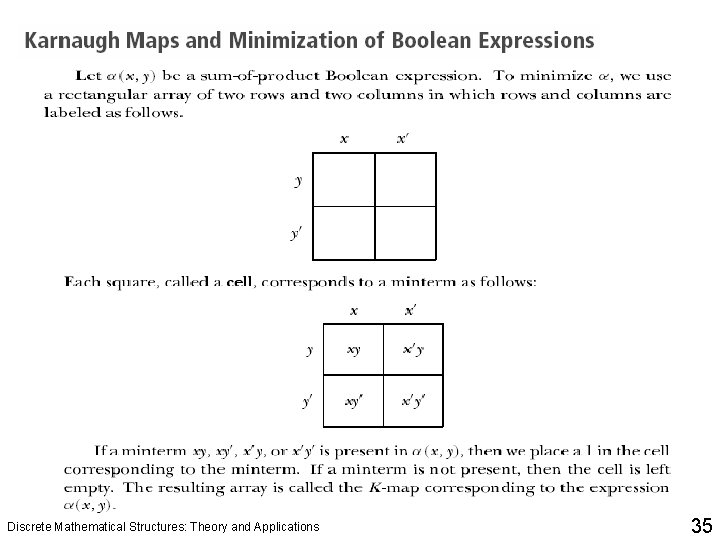
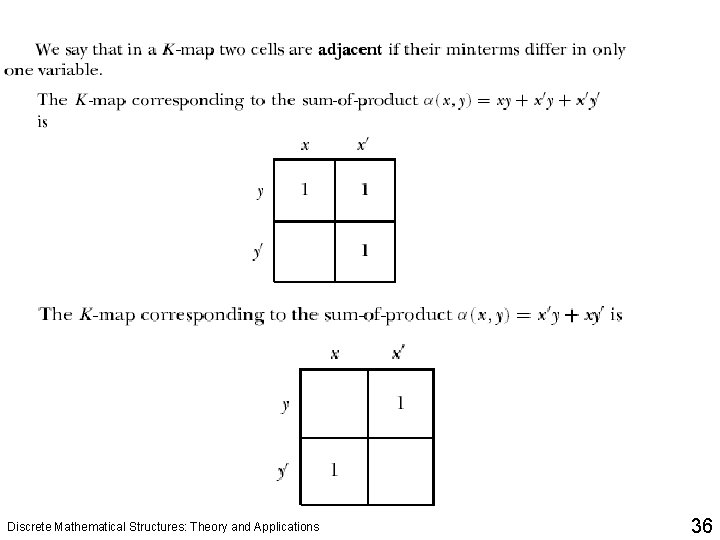
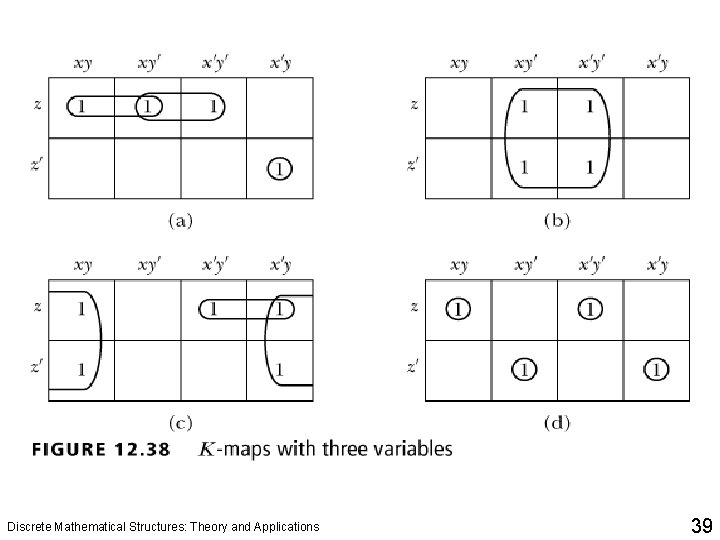
Logical Gates and Combinatorial Circuits q The Karnaugh map, or K-map for short, can be used to minimize a sum-of-product Boolean expression. Discrete Mathematical Structures: Theory and Applications 37

Discrete Mathematical Structures: Theory and Applications 38

Discrete Mathematical Structures: Theory and Applications 39

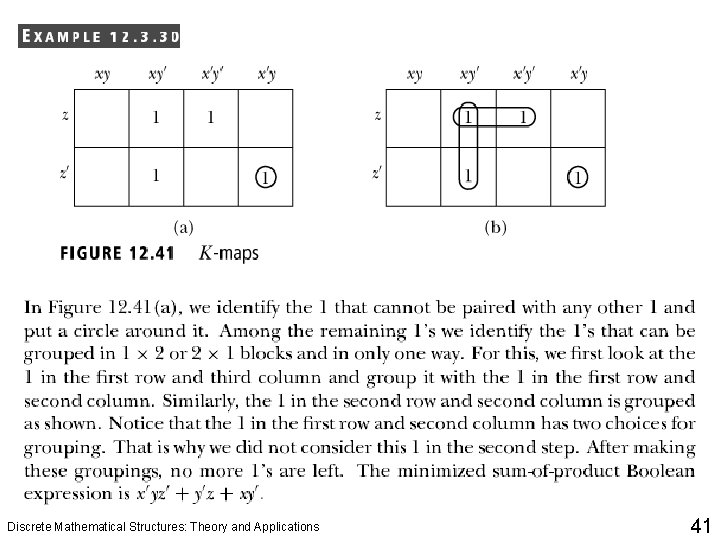
Logical Gates and Combinatorial Circuits 1. First mark the 1 s that cannot be paired with any other 1. Put a circle around them. 2. Next, from the remaining 1 s, find the 1 s that can be combined into two square blocks, i. e. , 1 x 2 or 2 x 1 blocks, and in only one way. 3. Next, from the remaining 1 s, find the 1 s that can be combined into four square blocks, i. e. , 2 x 2, 1 x 4, or 4 x 1 blocks, and in only one way. 4. Next, from the remaining 1 s, find the 1 s that can be combined into eight square blocks, i. e. , 2 x 4 or 4 x 2 blocks, and in only one way. 5. Next, from the remaining 1 s, find the 1 s that can be combined into 16 square blocks, i. e. , a 4 x 4 block. (Note that this could happen only for Boolean expressions involving four variables. ) 6. Finally, look at the remaining 1 s, i. e. , the 1 s that have not been grouped with any other 1. Find the largest blocks that include them. Discrete Mathematical Structures: Theory and Applications 40

Discrete Mathematical Structures: Theory and Applications 41