Chapter 1 Whole Numbers 1 1 Introduction to

Chapter 1 Whole Numbers

1. 1 Introduction to Numbers, Notation and Rounding • Definitions Numbers : Amounts or quantities Set: A group of elements Natural Numbers : 1, 2, 3, 4, 5, …. Whole Numbers : 0, 1, 2, 3, ….

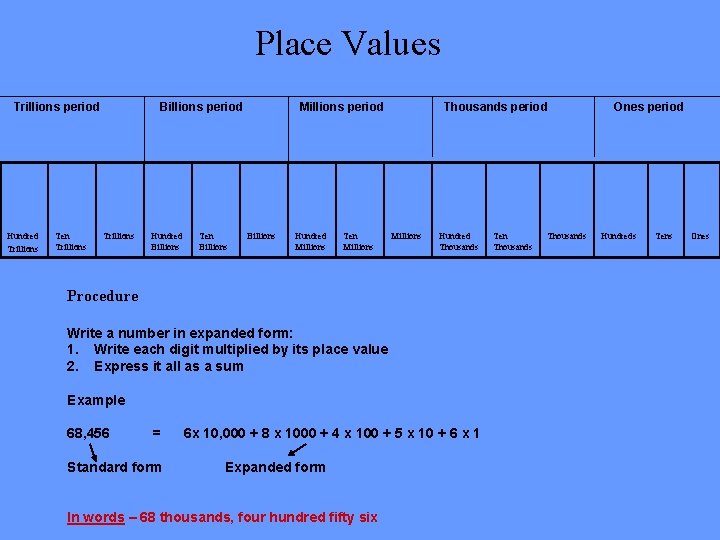
Place Values Trillions period Hundred Trillions Ten Trillions Billions period Trillions Hundred Billions Ten Billions Millions period Billions Hundred Millions Ten Millions Thousands period Millions Hundred Thousands Procedure Write a number in expanded form: 1. Write each digit multiplied by its place value 2. Express it all as a sum Example 68, 456 = Standard form 6 x 10, 000 + 8 x 1000 + 4 x 100 + 5 x 10 + 6 x 1 Expanded form In words – 68 thousands, four hundred fifty six Ten Thousands Ones period Hundreds Tens Ones

Use < , > , or = to make a true statement Definition Equation: A mathematical statement that contains an equal sign Example 14 = 14 is an equation, which is true 14 = 5 is not an equation , it is false, they are not equal Inequality: A mathematical statement that contains an inequality symbol. Greater than > Less than < 14 is greater than 12 14 > 12 12 is less than 14 12 < 14

Round numbers to a specified place Ø To round a number to a given place value, consider the digit to the right of the desired place value. Ø If this digit is 5 or greater, round up If this digit is 4 or less, round down Example 45, 685, 923 Millions 45, 685, 923 Hundred thousands Ten thousands 45, 685, 923 Hundreds 45, 685, 923 Tens

1. 2 Adding, subtracting, and solving equations with whole numbers Definition Addition : Arithmetic operation that combines amounts Commutative property of addition a + b = b + a, where a and b are any numbers Associative property of Addition ( a + b) + c = a + (b + c), where a, b, c are any numbers To add whole numbers: 1. Stack with corresponding place values aligned 2. Add the digits Example 1 1 3456 62345 +906 + 9039 4362 71384

Estimate sum Estimate the sum by rounding to the nearest Thousand, then find the actual sum. 52, 407 +31, 596 Estimate 52, 000 +32, 000 84, 000 Actual 52, 407 +31, 596 84, 003

Perimeter: The total distance around a shape. To find the perimeter of a shape, add the lengths of all the sides of the shape. 10 ft 8 ft 10 ft Variable: A symbol that can vary or change in value Constant: Any symbol that does not vary in value. P = 8 + 10 + 8 + 10= 36 ft

Subtraction To subtract whole number: 1. Stack the greater number on top of the smaller number, aligning the place values. 2. Subtract the digits in the bottom number from the digits directly above. If a digit in the top number is less than the digit beneath it, then rename the top digit. 14 9 9 3 4 10 10 13 45, 00 3 - 8, 36 5 Check by adding 36638 8365 Check by estimating 45, 000 - 8, 000 37, 000 36 6 3 8 45, 00 3 Keywords for subtraction Subtract, minus, remove, decreased by, difference, take away, left, less than

Procedure: To find a missing addend, write a related subtraction sentence. Subtract the known addend from the sum. Example 1 100 + x= 250 x = 250 – 100 = 150 Check 100+ 150 = 250 Example 2 65 + x= 93 x = 93 – 65 =28 Check 65 + 28 = 93 Definition Solution: A number that can replace the variable(s) in an equation and make the equation true

1. 3 Multiplying whole numbers and exponents Commutative property of multiplication a. b= b. a Associative property of multiplication Grouping three or more factors differently will not affect the product (ab)c= a(bc), where a, b, c are any real numbers Multiplicative property of 0 The product of 0 and a number is always 0 0. n = 0 and n. 0= 0, where n is any number Multiplicative property of 1 The product of 1 and a number is always the number 1. n = n and n. 1 = n, where n is any number Distributive Property If a sum or difference is multiplied by a number, then each number inside parenthesis may be multiplied by the number outside the paranthesis a(b+c) = ab + ac a(b – c) = ab – ac, where a, b and c are any numbers

Procedure To multiply two whole numbers, stack them and then apply the distributive property Multiply 503 x 62 1 503 X 62 1006 Multiply 2 times 503 + 3018 Multiply 6(tens) times 503 31, 186 Key words for multiplication Multiply, times, product, each, of , by

Exponent or power A symbol written to the upper right of a base number that indicates how many times to use the base as a factor. Base : The number that is repeatedly multiplied Base 28 Exponent = number of times the base is used as a factor 28 = 2. 2. 2 = 256 Exponential form Factored form Standard form

Powers of 10 and Period Names Period names 103 =1, 000 = One thousand 106 = 1, 000 = One million 109= 1, 000, 000 = One billion 1012= 1, 000, 000 = One trillion 1015= (1 with 15 zeros) = One quadrillion The names continue using the preceding pattern. Some names are rather colorful. 10100 = (1 with 100 zeros) = googol 10 googol = ( 1 with a googol of zeros)= googolplex

• Write in expanded form using powers of ten Example 1 3, 029, 408 = 3 x 106 + 0 x 105 +2 x 104 + 9 x 103 + 4 x 102 + 8 x 1 Example 2 24, 902 2 x 104 +4 x 103 + 9 x 102 + 2 x 1

1. 4 Dividing, square roots, and solving equations with whole numbers Division Property Ø When 1 is the divisor, the quotient is equal to the dividend n divided by 1 = n/1 =, where n is any number Ø When 0 is the divisor with any dividend other than 0, the quotient is undefined. n divided by 0, or n/0 , is undefined, when n = 0 Ø When 0 is the dividend, the quotient is 0 as long as the divisor is not also 0 0 divided n = 0/n , when n = 0 Ø If both dividend and divisor are 0, the quotient is indeterminate 0 divided 0 or 0/0 is indeterminate Ø When a number (other than 0) is divided by itself, the quotient is 1 n is divided by n = n/n = 1, when n = 0

Divisibility Rules a) 2 is an exact divisor for all even numbers. Even numbers have 0, 2, 4, 6, or 8 in the ones place Example- 2478 is divisible by 2 as even number 8 is in ones place b) To determine whether 3 is an exact divisor for a given number Add the digits in the dividend If the resulting sum is a number that is divisible by 3, then so is the dividend Example- 35, 616 is divisible by 3 as sum of the digits = 3 + 5 + 6 + 1 + 6= 21 divisible by 3 c) 5 is an exact divisor for numbers that have 0 or 5 in the ones place Example – 71, 315 is divisible by 5 because it has a 5 in the ones place

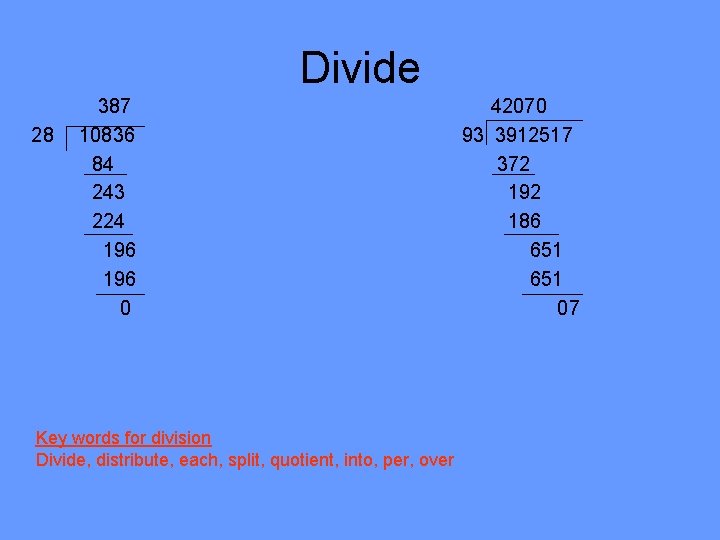
Divide 28 387 10836 84 243 224 196 0 Key words for division Divide, distribute, each, split, quotient, into, per, over 42070 93 3912517 372 192 186 651 07

Definition Square root : A base number that can be squared to equal a given number The symbol for square root is the radical sign. The number we wish to find the square root of is called the radicand Radical sign = 25 Perfect Square : A number that has a whole – number square root 25 2 = 625 Roots and their square Page 44

Order of Operations 1. Grouping symbols. These include parentheses( ), brackets[ ], braces{}, absolute value , radicals , and fraction bars ___ 2. Exponents 3. Multiplication or division from left to right, in order as they occur 4. Addition or subtraction from left to right, in order as they occur G Grouping E Exponents M D A S Multiplications Division Addition Subtraction or P Parenthesis E M D A S Exponents Multiplications Division Addition Subtraction

1. 6 Variables, Formulas, and Solving Equations Formula for Perimeter of a rectangle P = 2 L + 2 W L w w L To Use a formula 1. 2. Replace the variables with the corresponding given values Solve for the missing value

Use the formula to find Parallel lines : Straight lines that never intersect Parallelogram : A four sided figure with two pair of parallel sides The area of a parallelogram A = bh Right angle: An angle that measures 900 h b Volume of a Cube which is a measure of the amount of space inside a three-dimensional object. V= lwh h w l