Chapter 1 The Science of Physics 1 1

Chapter 1 The Science of Physics

1 -1: What is Physics? We are surrounded by the principles of physics in our everyday lives. Ø Any problem or question that deals with temperature, size, motion, position, shape or color involves physics. Ø

The Areas of Physics:

§ Classical Mechanics motion of macroscopic objects at low speeds (v << c) Examine motion & its causes. Ex: falling objects, weight, friction, etc.

Ø Thermodynamics deals with heat, work, temperature, and the statistical behaviour of a large number of particles

Ø Vibrations & Waves Deals with specific types of repetitive motion. Ex: springs, pendulums, sound…

Ø Optics Deals with light and its properties. Ex: mirrors, lenses, color…

Ø Electromagnetism theory of electricity, magnetism and electromagnetic fields Ex: electric charge, circuits, permanent magnets

Ø Relativity motion of objects at any speed, including very high speeds Ex: particle collisions, nuclear energy

Ø Quantum mechanics theory dealing with behaviour of particles at atomic levels

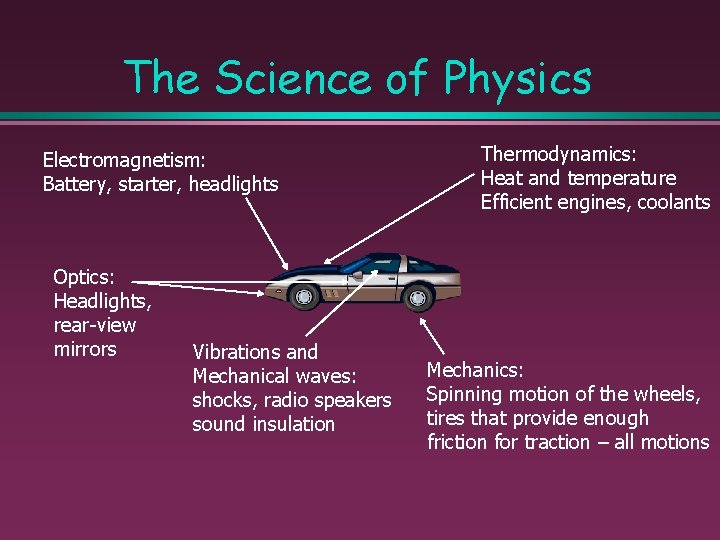
The Science of Physics Electromagnetism: Battery, starter, headlights Optics: Headlights, rear-view mirrors Vibrations and Mechanical waves: shocks, radio speakers sound insulation Thermodynamics: Heat and temperature Efficient engines, coolants Mechanics: Spinning motion of the wheels, tires that provide enough friction for traction – all motions

Scientific Method Ø Ø Make observations & collect data that lead to a question. Formulate and objectively test hypotheses by experiment. Interpret results, and revise hypothesis if necessary. State conclusions in a form that can be evaluated by others.

Models in physics Ø Ø A model is a replica or description designed to show the structure or workings of an object, system or concept. Simplify Help build hypotheses Guide experimental design Make testable predictions

1 -2: Measurement

Physical Quantity vs. Units Ø Ø Physical quantity- any characteristics of objects that can be measured. Ex: length, mass, temperature Units of measure- basic standards of measurement Ex: length can be measured in miles or meters

SI Standards UNIT Original standard Current standard Meter (length) 1/10, 000 distance from equator to North Pole Distance traveled by light in a vacuum in 3. 3 x 10 -9 s Kilogram (mass) Mass of 0. 0001 cubic meters of water Mass of a specific platinum-iridium alloy cylinder Second (time) (1/60)(1/24) = 0. 00001574 average solar days 9, 192, 631, 700 times the period of a radio wave from cesium-133

Other units are DERIVED units, that is, they are calculated from measurements in the base units. Ø Examples are velocity (m/s), acceleration (m/s 2), or density (g/cm 3). Ø

Prefixes Symbolize powers of 10 Ø Used to accommodate very large/small quantities Ø Commonly used prefixes on table 1 -3, pg. 12 Ø

Conversions Conversion factor- ratio used to convert from one unit or prefix to another Ø Used in the factor-label method to express answers in the desired units. Ø Example: 1 mile = 1. 61 km Ø

» Example: Convert 10. 0 miles into kilometers » Conversion factor: 1 mile = 1. 61 km Set up the conversion so that miles cancel when multiplied # km = 10. 0 mi x 1. 61 km = 16. 1 1 mile

Sample Problem Ø “Oh man, ” a bleary-eyed student once noted, “That lecture on classroom policies must have gone on for a microcentury. ” How many minutes are there in a microcentury?

Solution Ø Micro = 10 -6

Accuracy & Precision Ø Ø Accuracy- how close a measurement comes to accepted value Precision- degree of exactness, small variation between repeated measurements

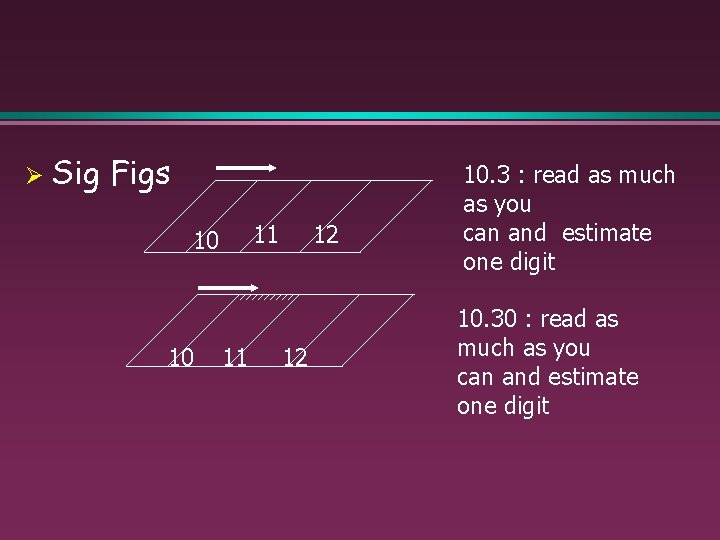
Measurement / Significant figures § § § Uncertainty in measurement depends on the quality of the apparatus, skill of the experimenter and number of measurements performed Sig figs keep track of imprecision Sig figs include all measured digits plus one estimated digit

Ø Sig Figs 11 10 10 11 12 12 10. 3 : read as much as you can and estimate one digit 10. 30 : read as much as you can and estimate one digit

The rules for significant digits 1. All whole number digits are significant. Ex. 1, 2, 3, 4, 5, 6, 7, 8, 9 245, 955 14, 328 96 6 significant digits ________________

The rules for significant digits 2. Rules for Zeros a. Zeros between other nonzero digits are significant. Example: 404 3 significant digits 40530004 _______ 60606 _______

The rules for significant digits b. Zeros in front of nonzero digits are not significant Ø Example Ø 00222 3 significant digits Ø 0. 00556 _______ Ø 000001 ______

The rules for significant digits c. Zeros that are at the end of a number and also to the right of the decimal are significant. Ø Example Ø 120. 00 5 significant digits Ø 4052. 00000 _______ Ø 30302. 0 _______

The rules for significant digits d. Zeros at the end of a number without a decimal are not significant. Ø Example Ø 300 1 significant digit Ø 46000 _______ Ø 460. 00 _______

The rules for significant digits in calculations 1. Addition or subtraction - The final answer should have the same number of digits to the right of the decimal as the measurement with the smallest number of digits to the right of the decimal.

Example Ø 4. 02 + 6. 11+ 4. 9 = 15. 0 (15. 03) Ø 6. 111 + 12. 31 + 1. 2 = _____ Ø 10. 256 – 2. 44 – 1. 6 = ____

The rules for significant digits in calculations 2. Multiplication or division – the final answer has the same number of significant figures as the measurement having the smallest number of significant figures.

Example Ø 4. 0 x 2. 11 x 3. 456 = 29 (actual answer is 29. 16864) Ø 4. 01 x 4. 1 / 4. 012 = _______ Ø 16. 211 / 4. 211 / 2 = _______

Scientific Notation § § § Scientific Notation- in the form of A x 10 n 1< A< 10 and n = power of 10 A contains only sig figs of original number/measurement

1 -3: Language of Physics Tables, Graphs, & Equations

Tables, graphs & equations make data easier to understand Ø Equations used to describe relationship between physical quantities Ø Appendix B pg 952 -960 lists variables, symbols & constants used Ø

Dimensional Analysis Ø Ø Dimensional analysis used to: - check a specific formula - give hints as to the correct form the equations must take Dimensional analysis does not give any information on the magnitude of the constants of proportionality

Orders-of-Magnitude Refers to the nearest power of 10 Ø Useful to compute an approximate answer Ø Results can be used to decide whether a more precise calculation is necessary Ø Assumptions are usually needed Ø