Chapter 1 Straight Lines and Linear Functions The












- Slides: 14

Chapter 1. Straight Lines and Linear Functions • The Cartesian Coordinate System • Straight Lines • Linear Functions and Mathematical Models • Intersection of Straight Lines • The Method of Least Squares (Optional) Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

1. 1 The Cartesian Coordinate System • Real numbers may be represented geometrically by points on a line. This line is called the real number line, or coordinate line. • We can construct the real number line as follows: – Select the number 0 (such point is called the origin). – Determine the scale. – Each positive (negative) real number x lies x units to the right (left) of 0. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

The Real Numbers The real numbers can be ordered and represented in order on a number line 0 -1. 87 4. 55 x -3 -2 -1 0 1 2 3 4 Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

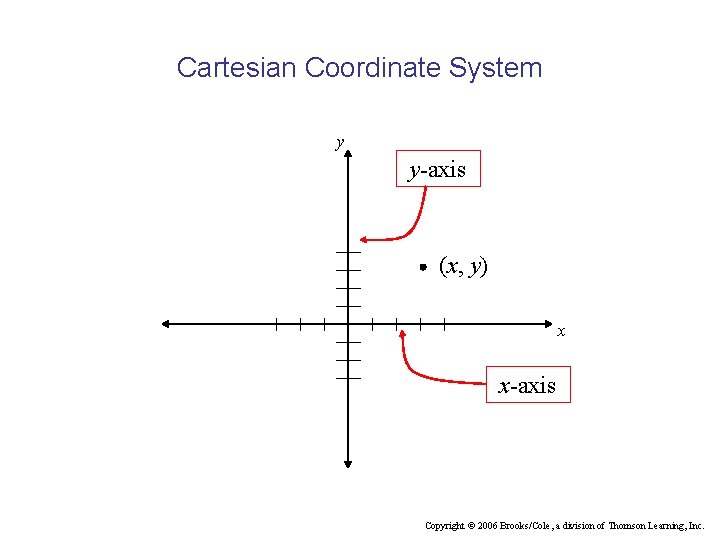
Cartesian Coordinate System • • • Take two perpendicular lines These lines intersect at 0, called the origin. The horizontal line is called the x-axis The vertical line is called the y-axis. A number scale is set alone the x-axis, with positive numbers lying to the right of the origin and negative numbers lying to the left of the origin, similarly for the yaxis. • The two number scales need not be the same. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

We can represent a point in the plane uniquely by an ordered pair of numbers: (x, y) • Give a point P, we can find an ordered pair (x, y) corresponding to it by drawing perpendiculars from P to the x-axis and y-axis. • Conversely, given an ordered pair (x, y), we can located the point P. • In the ordered pair (x, y), x is called the x-coordinate, y is called the y- coordinate. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Cartesian Coordinate System y y-axis (x, y) x x-axis Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Cartesian Coordinate System y Ex. Plot (4, 2) Ex. Plot (-2, -1) Ex. Plot (2, -3) (4, 2) x (-2, -1) (2, -3) Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

The Quadrants The axes divide the plane into four quadrants. • Quadrant I consists of P (x, y) with x>0 and y>0 • Quadrant II consists of P (x, y) with x<0 and y>0 • Quadrant III consists of P (x, y) with x<0 and y<0 • Quadrant IV consists of P (x, y) with x>0 and y<0 Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Cartesian Coordinate System Quadrants… y II I x III IV Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

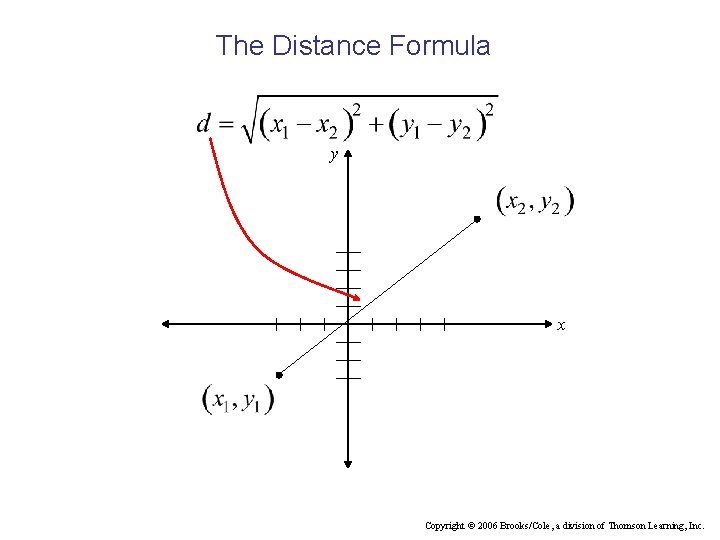
The Distance Formula • The distance d between two points P 1(x 1, y 1) and P 2(x 2, y 2) in the plane is given by Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

The Distance Formula y x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Examples Find the distance between (7, 5) and (-3, -2) Solution Let (7, 5) and (-3, -2) be points in the plane. We have x 1 = 7 y 1 = 5 x 2 = -3 y 2 = -2 Using the distance formula, we have

The Equation of a Circle A circle with center (h, k) and radius of length r can be expressed in the form: Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Examples Find an equation of the circle with radius 3 and center (-4, 1). Solution We use the circle formula with r = 3, h = -4, and k = 1: x