CHAPTER 1 SINUSOID PHASOR DMT 122 CIRCUIT THEORY

CHAPTER 1 SINUSOID & PHASOR DMT 122 CIRCUIT THEORY 2 SEMESTER 2 2018/2019

CONTENT 01 The different between DC and AC 02 Understand cycle, period and frequency of sinusoid 03 Phase relationship of waveforms using phasors 04 Complex number & phasors 05 Lead & lag relationship with phasors and sinusoids

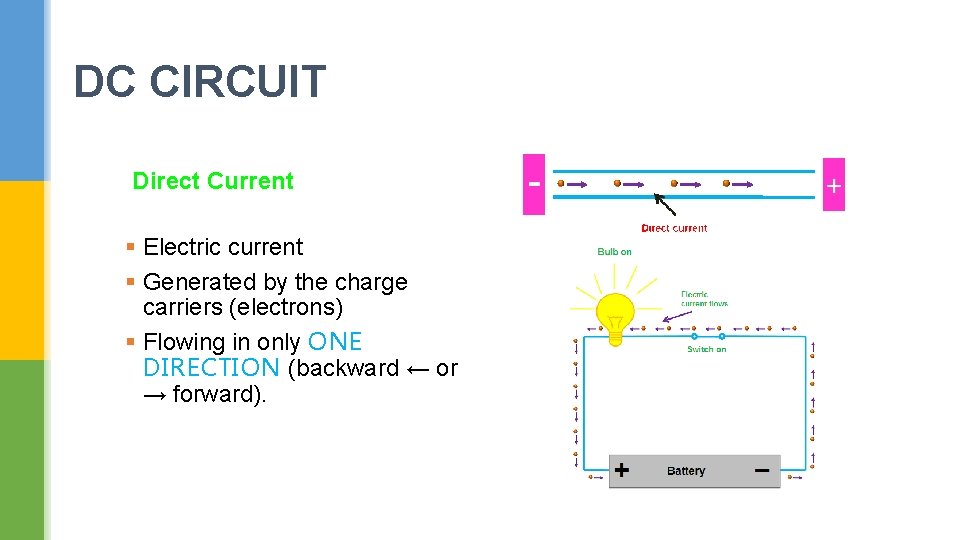
DC CIRCUIT Direct Current § Electric current § Generated by the charge carriers (electrons) § Flowing in only ONE DIRECTION (backward ← or → forward).

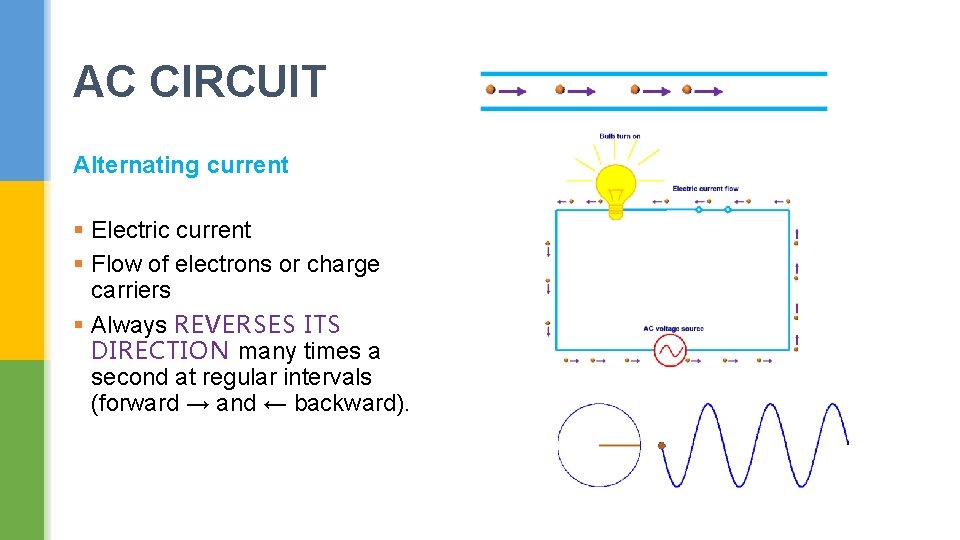
AC CIRCUIT Alternating current § Electric current § Flow of electrons or charge carriers § Always REVERSES ITS DIRECTION many times a second at regular intervals (forward → and ← backward).

DIFFERENT BETWEEN AC AND DC AC CURRENT § Electric charges its direction PERIODLY § Generating frequencies is 50 Hz – 60 Hz § Magnitude of current varying with time § Source of AC current is GENERATOR § Have resistance with capacitor & inductor § The waveform are SINUSOIDAL, TRIANGULAR, SQUARE DC CURRENT § Electric charge flow only in ONE direction § The frequencies is ZERO § Magnitude of current varying with time is CONSTANT § Source of DC current is BATTERY / CELL § Have ONLY resistance § The waveform are PURE and PULSATING

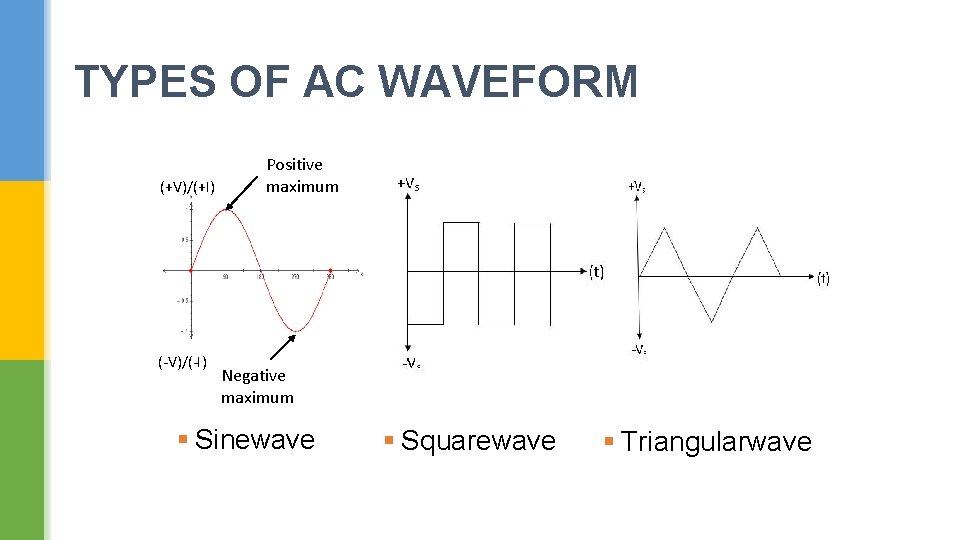
TYPES OF AC WAVEFORM (+V)/(+I) (-V)/(-I) Positive maximum Negative maximum § Sinewave § Squarewave § Triangularwave

SINUSOIDS §

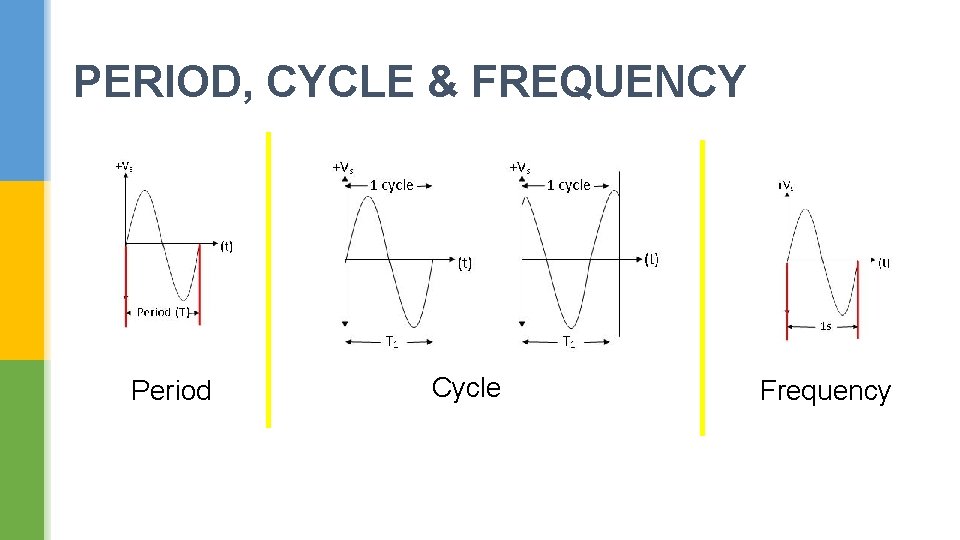
PERIOD, CYCLE & FREQUENCY Period Cycle Frequency

PERIOD & FREQUENCY RELATIONSHIP §

EXAMPLE 1 §

EXAMPLE 2 §

TRIGONOMETRIC IDENTITIES

PHASOR § ?

PHASOR § If we were to rotate a phasor and plot the vertical component, it would graph a sine wave. § Phasors are used to compare phase differences. § The magnitude of the phasor is the Amplitude (peak) § The angle measurement used is the PHASE ANGLE,

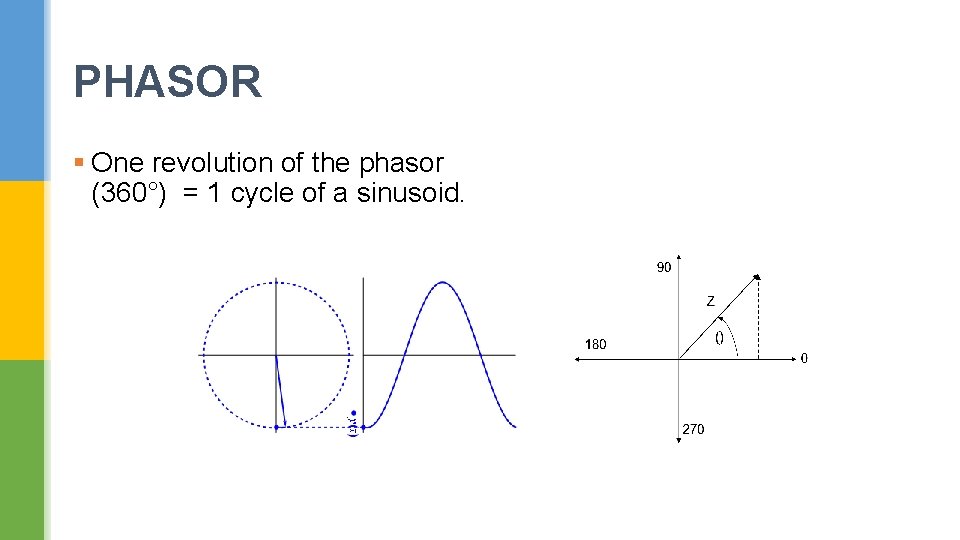
PHASOR § One revolution of the phasor (360°) = 1 cycle of a sinusoid.

TIME DOMAIN PHASOR DOMAIN §

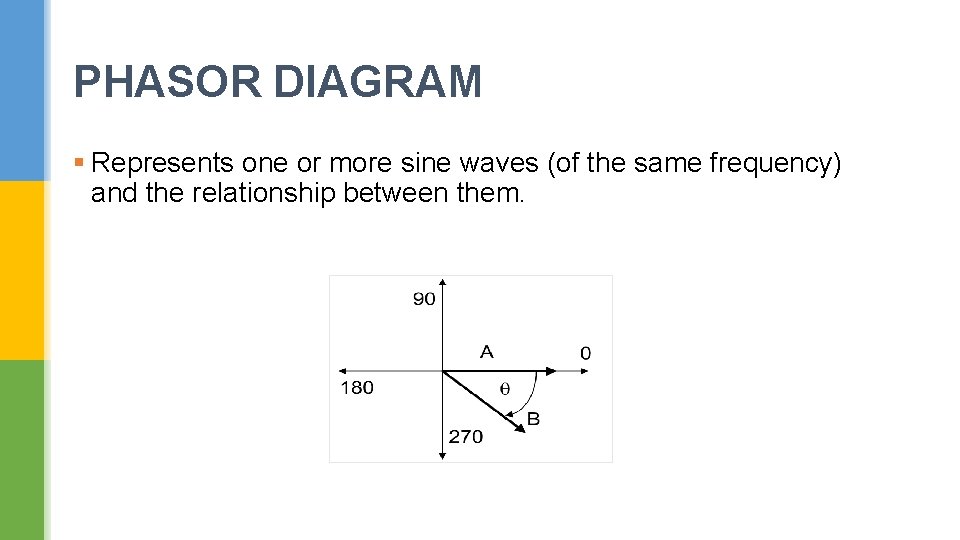
PHASOR DIAGRAM § Represents one or more sine waves (of the same frequency) and the relationship between them.

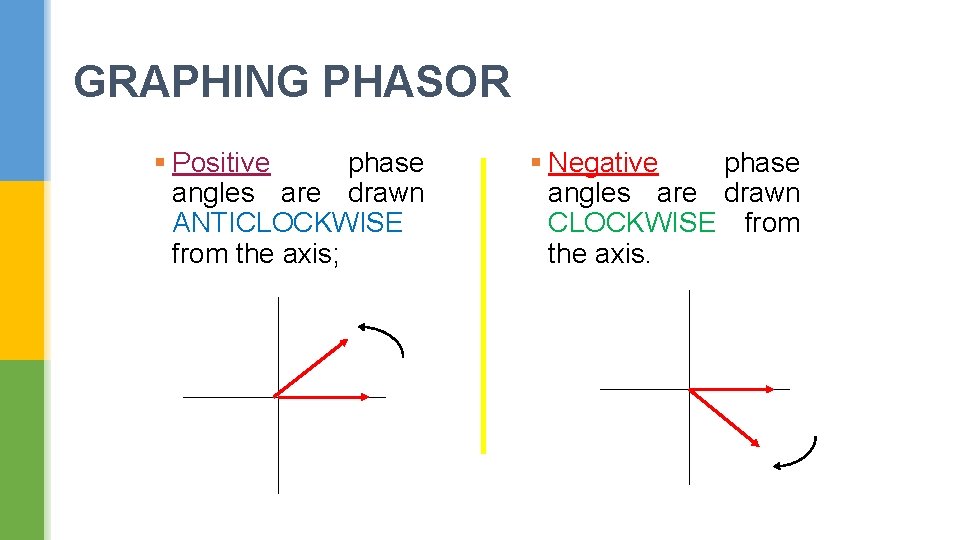
GRAPHING PHASOR § Positive phase angles are drawn ANTICLOCKWISE from the axis; § Negative phase angles are drawn CLOCKWISE from the axis.

LEADING & LAGGING § Leading and lagging current : phenomena that occur as a result of alternating current. § The value of voltage and current vary sinusoidally. § The terms lead, lag, or in phase are used to describe current with reference to voltage.

LEADING & LAGGING § Lagging current : an alternating current that reaches its maximum value up to 90 degrees behind the voltage that produces it. § Leading current : an alternating current that reaches its maximum value up to 90 degrees ahead of the voltage that it produces.

EXAMPLE 3 §

EXAMPLE 4 §

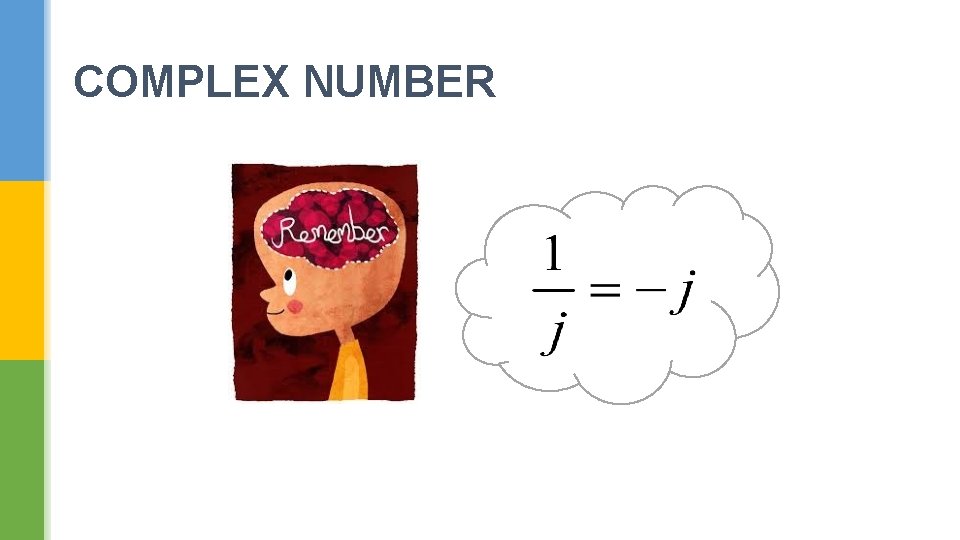
COMPLEX NUMBER § Complex numbers contain real and imaginary (“j”) components. § Express in: § Rectangular coordinates (x+jy) § Polar coordinates - phasors

COMPLEX NUMBER : MATH OPERATION § Addition § Subtraction

COMPLEX NUMBER : MATH OPERATION § Multiplication § Division

COMPLEX NUMBER

EXAMPLE 5 § Evaluate these complex numbers:

EXAMPLE 5