CHAPTER 1 SETS What is a Set A

CHAPTER 1 SETS

What is a Set? A set is a well-defined collection of distinct objects. ¡ The objects in a set are called the elements or members of the set. ¡ Capital letters A, B, C, … usually denote sets. ¡ Lowercase letters a, b, c, … denote the elements of a set. ¡

Examples ¡ ¡ ¡ The collection of the vowels in the word “probability”. The collection of real numbers that satisfy the equation. The collection of two-digit positive integers divisible by 5. The collection of great football players in the National Football League. The collection of intelligent members of the United States Congress.

The Empty Set The set with no elements. ¡ Also called the null set. ¡ Denoted by the symbol f. ¡ Example: The set of real numbers x that satisfy the equation ¡

Finite and Infinite Sets A finite set is one which can be counted. ¡ Example: The set of two-digit positive integers has 90 elements. ¡ An infinite set is one which cannot be counted. ¡ Example: The set of integer multiples of the number 5. ¡

The Cardinality of a Set ¡ ¡ ¡ Notation: n(A) For finite sets A, n(A) is the number of elements of A. For infinite sets A, write n(A)=∞.

Specifying a Set ¡ List the elements explicitly, e. g. , ¡ List the elements implicitly, e. g. , ¡ Use set builder notation, e. g. ,

The Universal Set A set U that includes all of the elements under consideration in a particular discussion. ¡ Depends on the context. ¡ Examples: The set of Latin letters, the set of natural numbers, the set of points on a line. ¡

The Membership Relation Let A be a set and let x be some object. ¡ Notation: ¡ Meaning: x is a member of A, or x is an element of A, or x belongs to A. ¡ Negated by writing ¡ Example: . , . ¡

Equality of Sets ¡ ¡ Two sets A and B are equal, denoted A=B, if they have the same elements. Otherwise, A≠B. Example: The set A of odd positive integers is not equal to the set B of prime numbers. Example: The set of odd integers between 4 and 8 is equal to the set of prime numbers between 4 and 8.

Subsets ¡ ¡ ¡ A is a subset of B if every element of A is an element of B. Notation: For each set A, For each set B, A is proper subset of B if and

Unions ¡ The union of two sets A and B is ¡ The word “or” is inclusive.

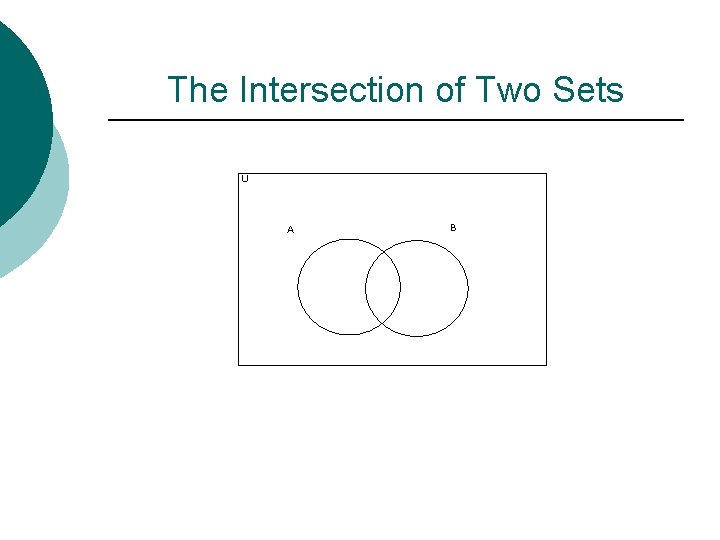
Intersections ¡ The intersection of A and B is ¡ Example: Let A be the set of even positive integers and B the set of prime positive integers. Then ¡ Definition: A and B are disjoint if

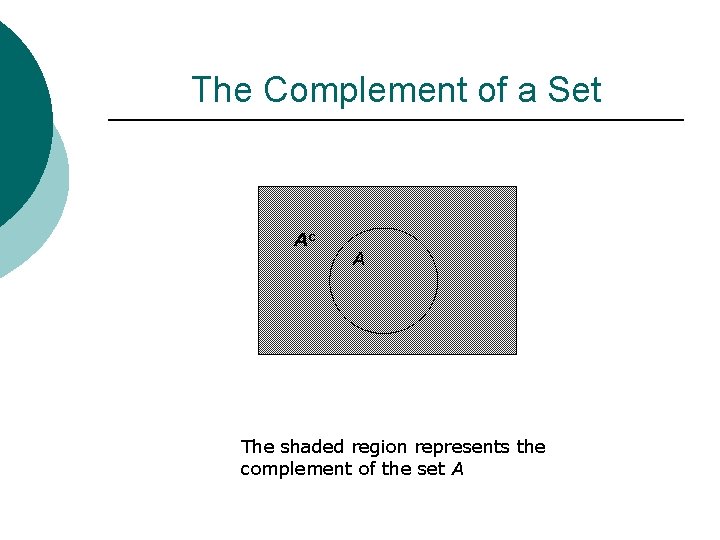
Complements o If A is a subset of the universal set U, then the complement of A is the set o Note: ;

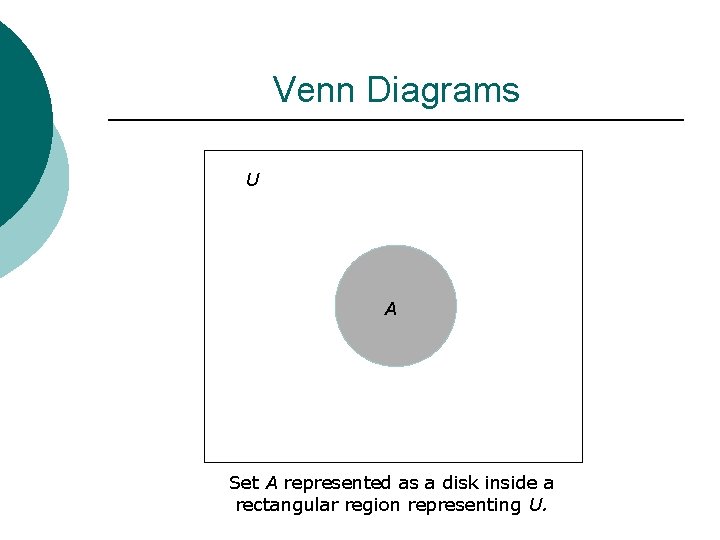
Venn Diagrams U A Set A represented as a disk inside a rectangular region representing U.

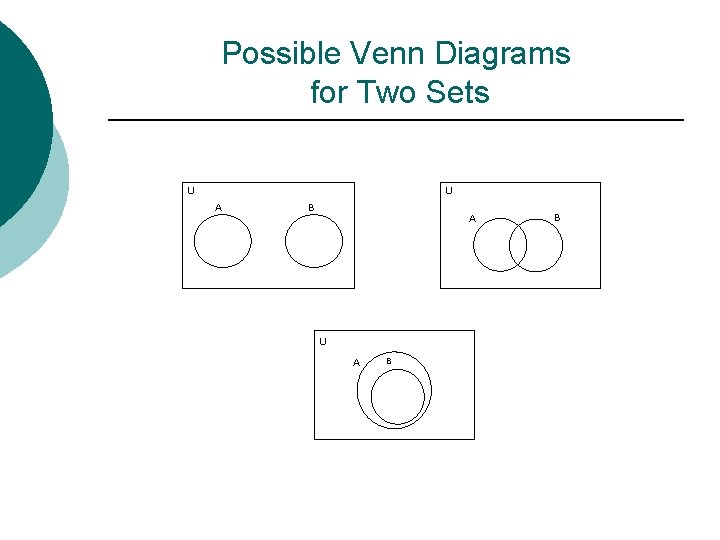
Possible Venn Diagrams for Two Sets U U A B A U A B B

The Complement of a Set Ac A The shaded region represents the complement of the set A

The Union of Two Sets U A B

The Intersection of Two Sets U A B

Sets Formed by Two Sets o ¡ U B A R 1 R 2 R 3 ¡ R 4 ¡

Two Basic Counting Rules If A and B are finite sets, 1. 2. See the preceding Venn diagram.