Chapter 1 Section 3 Solving Equations Verbal Expressions

Chapter 1 Section 3 Solving Equations

Verbal Expressions to Algebraic Expressions • Example 1: Write an algebraic expression to represent each variable expression. a) 7 less than a number b) Three times the square of a number c) The cube of a number increased by 4 times the same number

Your turn: • Write an algebraic expression to represent each variable expression. 1) 3 more than a number 2) Six times the cube of a number 3) The square of a number decreased by the product of 5 and the number 4) Twice the difference of a number and 6

Algebraic to Verbal • Example 2: Write a verbal sentence to represent each equation. a) 10 = 12 – 2 b) n + (-8) = -9 c) n/6 = n 2

Your turn: • Write a verbal sentence to represent each equation. 4) 14 + 9 = 23 5) 6 = -5 + x 6) 7 y – 2 = 19

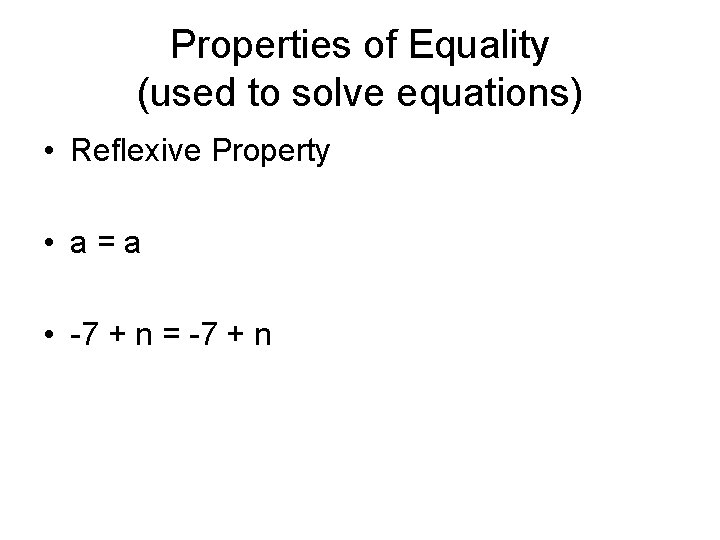
Properties of Equality (used to solve equations) • Reflexive Property • a=a • -7 + n = -7 + n

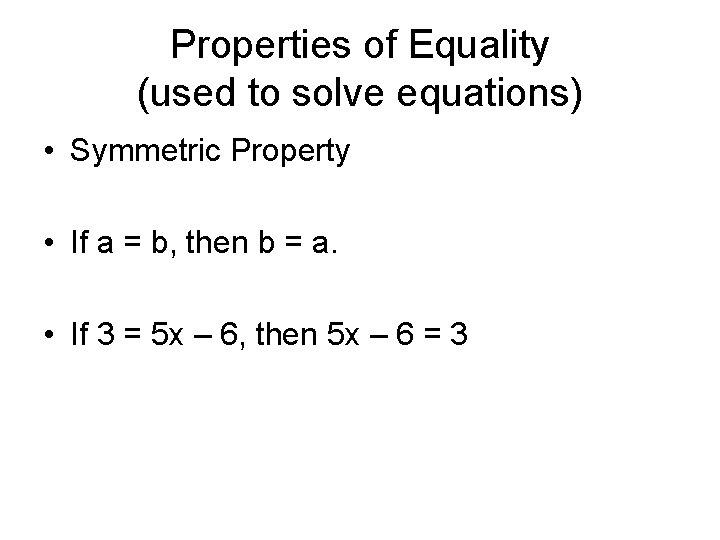
Properties of Equality (used to solve equations) • Symmetric Property • If a = b, then b = a. • If 3 = 5 x – 6, then 5 x – 6 = 3

Properties of Equality (used to solve equations) • Transitive Property • If a = b and b = c, then a = c. • If 2 x + 1 = 7 and 7 = 5 x – 8, then 2 x + 1 = 5 x – 8

Properties of Equality (used to solve equations) • Substitution Property • If a = b, then a may be replaced by b and b may be replaced by a • If (4 + 5)m = 18, then 9 m = 18

Example 3: • Name the property illustrated by each statement. a) If 3 m = 5 n and 5 n = 10 p, then 3 m = 10 p b) If -11 a + 2 = -3 a, then -3 a = -11 a + 2

Your turn: • Name the property illustrated by each statement. 7) If xy = 28 and x = 7, then 7 y = 28 8) a – 2. 03 = a – 2. 03

More Properties… • Addition & Subtraction Properties of Equality • Multiplication & Division Properties of Equality • (Both more or less say that an equation can be solved by adding, subtracting, multiplying, or dividing the same number from each side of the equation. )

Example 4: • Solve each equation. Check your solution. a) a + 4. 39 = 76 b) -3/5 d = 18

Your Turn: • Solve each equation. Check your solution. 9) s – 5. 48 = 0. 02 10) 18 = ½ t

Example 5: • Solve 2(2 x + 3) – 3(4 x – 5) = 22

Your Turn: 11) Solve 53 = 3(y - 2) – 2(3 y - 1)

Assignment: p. 24 # 20 -24 even, 27 -28, 30, 32, 35 -39, 42 -52 even