Chapter 1 Section 1 5 Segments and Angle

Chapter 1 Section 1. 5 Segments and Angle Bisectors

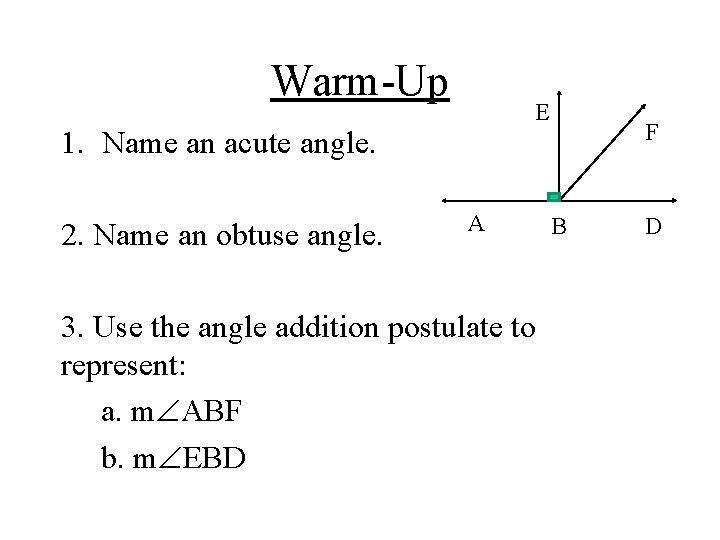
Warm-Up E 1. Name an acute angle. 2. Name an obtuse angle. A 3. Use the angle addition postulate to represent: a. m ABF b. m EBD F B D

Midpoint • The midpoint of a segment is the point that divides the segment into two congruent segments • Bisect: – Two cut a figure in half A B C Midpoint Since B is the midpoint of , then

Segment Bisector • A segment, ray, line or plane that intersects a segment at its midpoint Midpoint P Segment Bisector • C Q R • D Since is the Segment Bisector of , then

Use a ruler to measure the segment, and redraw the line segment. Then construct a segment bisector.

Midpoint formula • Used to find the midpoint of a segment with known endpoints If A(x 1, y 1) and B(x 2, y 2) are the endpoints of segment AB, then the midpoint of segment AB has coordinates

Find the coordinates of the midpoint of a segment with the given endpoints 1. A(-3, 5) and B(5, -1) § Use the formula 2. C(-4, -3) and D(6, 3) § Use the formula

Find the coordinates of the other endpoint of the segment with the given endpoint and midpoint M • T(4, 1) and M(3, 0) – Use the formula – Remember the other endpoint is (x 2, y 2) 1. Find x 2 2. Find y 2 The other endpoint is .

Find the coordinates of the other endpoint of the segment with the given endpoint and midpoint M • T(-4, 3) and M(-1, -5) – Use the formula – Remember the other endpoint is (x 2, y 2) 1. Find x 2 2. Find y 2 The other endpoint is .

Angle Bisector • A ray that divides an angle into two congruent adjacent angles B • • P A • C If is the angle bisector of BAC, then BAP PAC

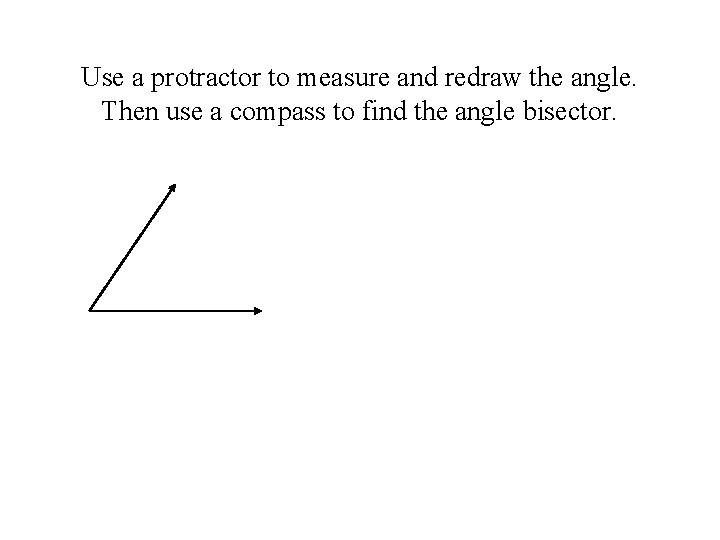
Use a protractor to measure and redraw the angle. Then use a compass to find the angle bisector.

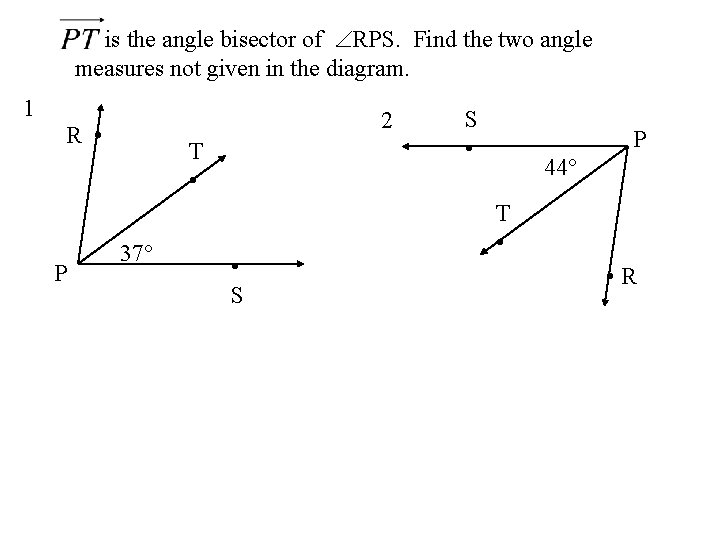
is the angle bisector of RPS. Find the two angle measures not given in the diagram. 1 2 R • P T • 37° • S S • P 44° T • • R

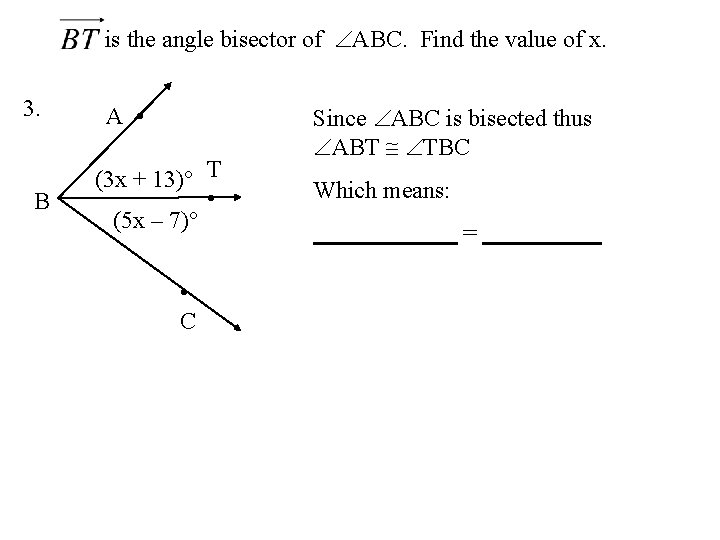
is the angle bisector of ABC. Find the value of x. 3. B A • (3 x + 13)° T • (5 x – 7)° • C Since ABC is bisected thus ABT TBC Which means: =