Chapter 1 Section 1 3 Segments and Their

Chapter 1 Section 1. 3 Segments and Their Measures

More Definitions • Postulate/Axiom – Rules that are accepted without proof • Example: The sun rise postulate – Tomorrow the sun will rise in the east.

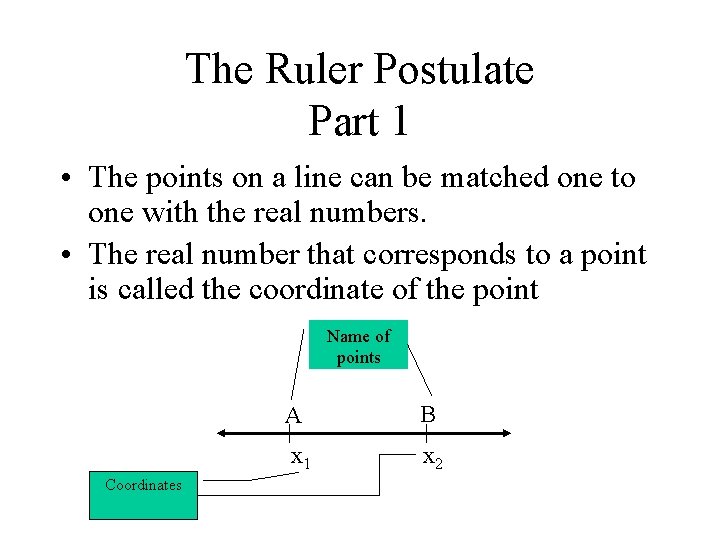
The Ruler Postulate Part 1 • The points on a line can be matched one to one with the real numbers. • The real number that corresponds to a point is called the coordinate of the point Name of points Coordinates A B x 1 x 2

Ruler Postulate Part 2 • The distance between points A and B, is the absolute value of the difference between the coordinates of A and B • The length of is denoted by AB A B x 1 x 2 AB = |x 2 – x 1|

Ruler Postulate in a nut shell • You can use a ruler to find the coordinates of points on a line. • You can subtract the coordinates of points on a line to find the distance between them.

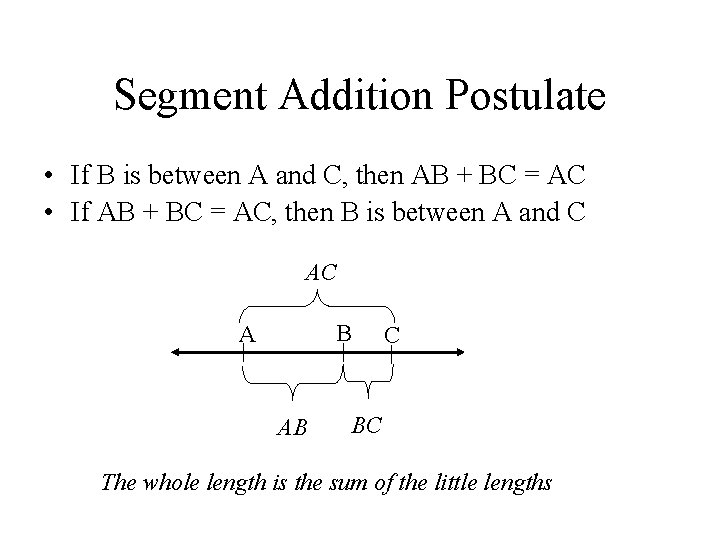
Segment Addition Postulate • If B is between A and C, then AB + BC = AC • If AB + BC = AC, then B is between A and C AC B A AB C BC The whole length is the sum of the little lengths

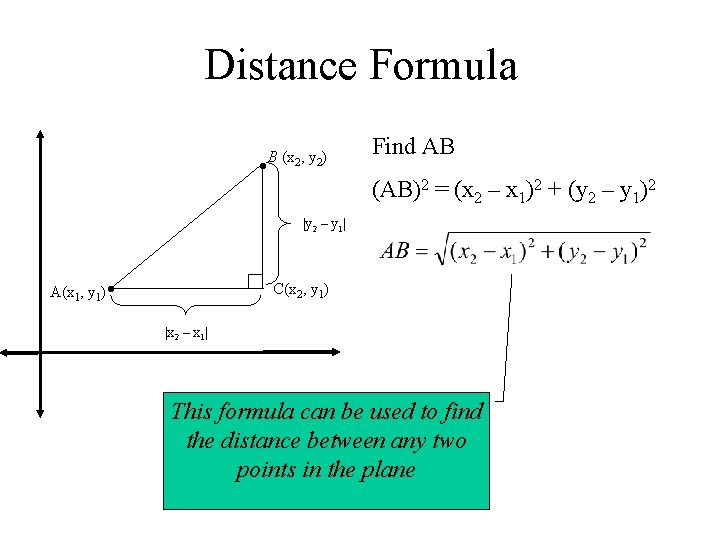
Distance Formula • B (x 2, y 2) Find AB (AB)2 = (x 2 – x 1)2 + (y 2 – y 1)2 |y 2 – y 1| A(x 1, y 1) • C(x 2, y 1) |x 2 – x 1| This formula can be used to find the distance between any two points in the plane

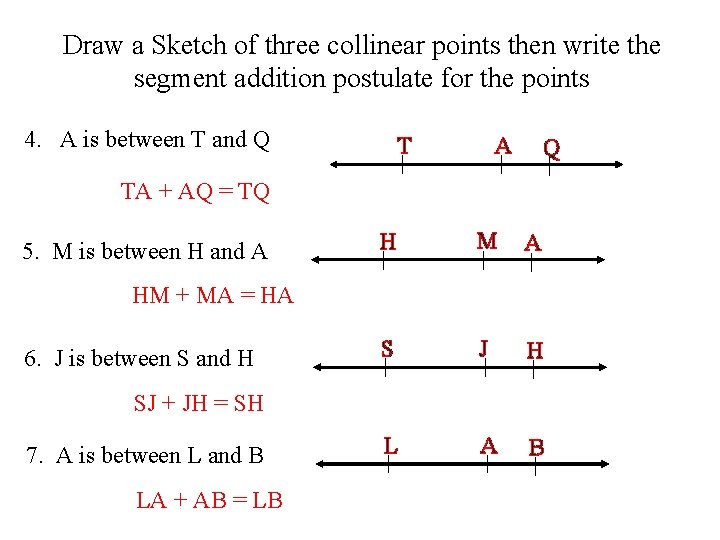
Draw a Sketch of three collinear points then write the segment addition postulate for the points 4. A is between T and Q A T Q TA + AQ = TQ 5. M is between H and A H M A S J H L A B HM + MA = HA 6. J is between S and H SJ + JH = SH 7. A is between L and B LA + AB = LB

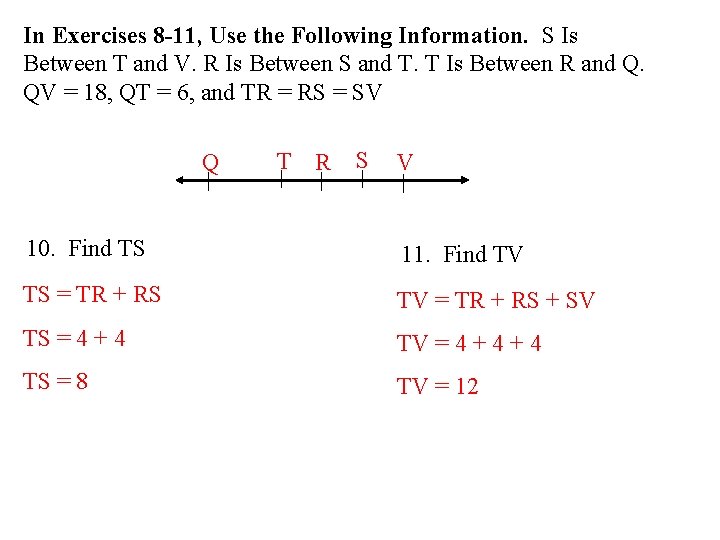
In Exercises 8 -11, Use the Following Information. S Is Between T and V. R Is Between S and T. T Is Between R and Q. QV = 18, QT = 6, and TR = RS = SV Q T R S V 8. Find RS 9. Find QS QV = QT + TR + RS + SV QS = QT + TR + RS 18 = 6 + RS QS = 6 + 4 12 = 3 RS QS = 14 4 = RS

In Exercises 8 -11, Use the Following Information. S Is Between T and V. R Is Between S and T. T Is Between R and Q. QV = 18, QT = 6, and TR = RS = SV Q T R S V 10. Find TS 11. Find TV TS = TR + RS TV = TR + RS + SV TS = 4 + 4 TV = 4 + 4 TS = 8 TV = 12

Suppose J is between H and K, use the segment addition postulate to solve for x then find the length of each segment H J K 12. HJ = 2 x + 4 JK = 3 x + 3 KH = 22 HJ + JK = HK 2 x + 4 + 3 x + 3 = 22 5 x + 7 = 22 5 x = 15 x=3 HJ = 2(3) + 4 = 10 JK = 3(3) + 3 = 12

Suppose J is between H and K, use the segment addition postulate to solve for x then find the length of each segment H J K 13. HJ = 5 x - 3 JK = 8 x - 9 KH = 131 HJ + JK = HK 5 x - 3 + 8 x - 9 = 131 13 x - 12 = 131 13 x = 143 x = 11 HJ = 5(11) – 3 = 52 JK = 8(11) - 9 = 79

Find the distance between each pair of points 15. D(1, 3), E(-2, 4), F(0, -4) Find ED Find DF Find EF

Find the distance between each pair of points 16. G(-1, 0), H(2, -4), I(1, 3) Find GH Find GI Find HI