Chapter 1 Random Process 1 1 Introduction Physical















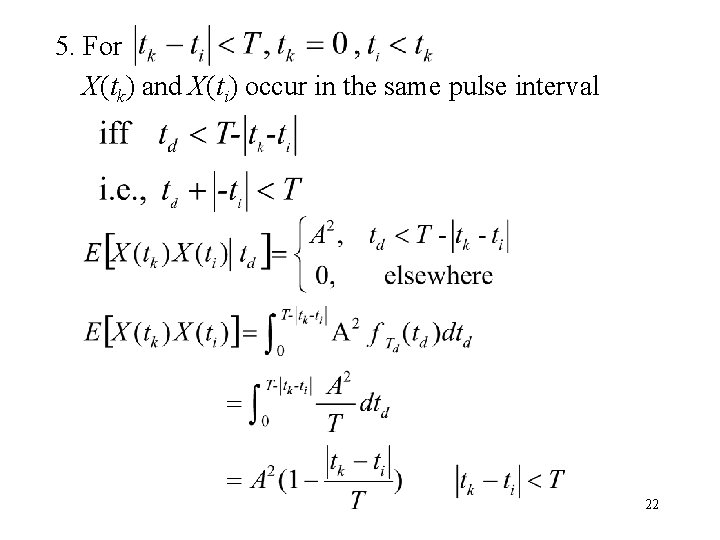

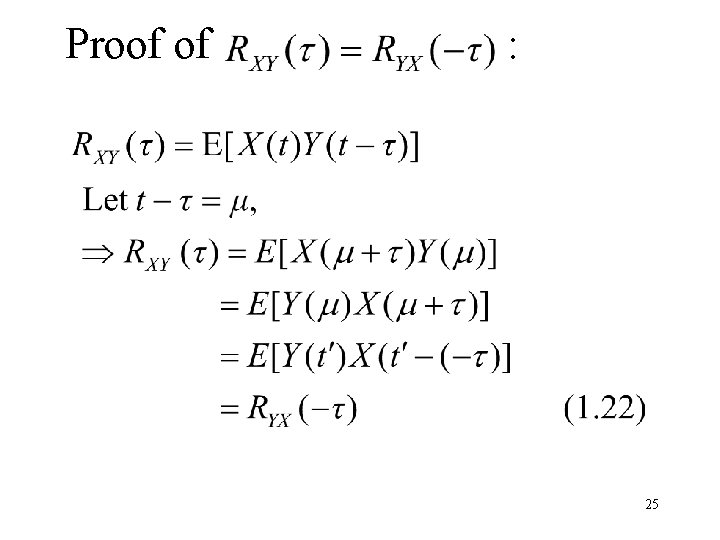

























- Slides: 61

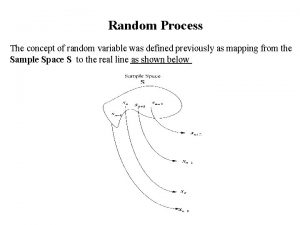
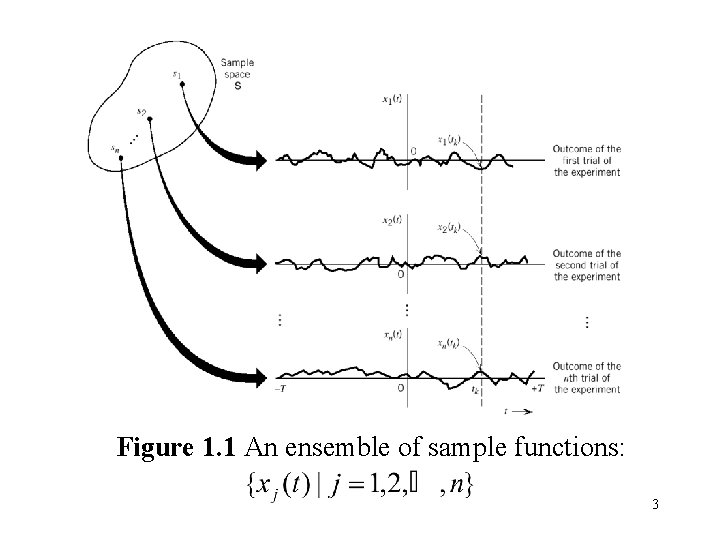
Chapter 1 Random Process 1. 1 Introduction (Physical phenomenon) Deterministic model : No uncertainty about its timedependent behavior at any instant of time. Random model : The future value is subject to “chance”(probability) Example: Thermal noise , Random data stream 1. 2 Mathematical Definition of a Random Process (RP) The properties of RP a. Function of time. b. Random in the sense that before conducting an experiment, not possible to define the waveform. Sample space S function of time, X(t, s) mapping 1

(1. 1) 2 T: The total observation interval (1. 2) = sample function At t = tk, xj (tk) is a random variable (RV). To simplify the notation , let X(t, s) = X(t): Random process, an ensemble of time function together with a probability rule. Difference between RV and RP RV: The outcome is mapped into a number RP: The outcome is mapped into a function of time 2

Figure 1. 1 An ensemble of sample functions: 3

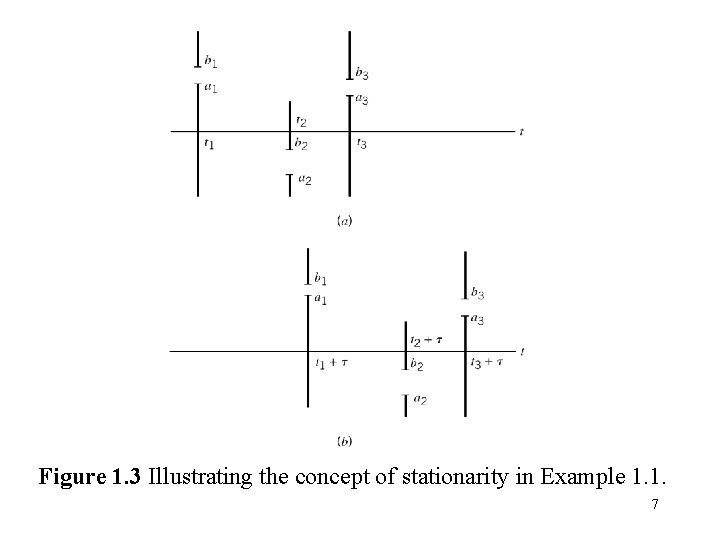
1. 3 Stationary Process : The statistical characterization of a process is independent of the time at which observation of the process is initiated. Nonstationary Process: Not a stationary process (unstable phenomenon ) Consider X(t) which is initiated at t = , X(t 1), X(t 2)…, X(tk) denote the RV obtained at t 1, t 2…, tk For the RP to be stationary in the strict sense (strictly stationary) The joint distribution function (1. 3) For all time shift , all k, and all possible choice of t 1, t 2…, tk 4

X(t) and Y(t) are jointly strictly stationary if the joint finite-dimensional distribution of and are invariant w. r. t. the origin t = 0. Special cases of Eq. (1. 3) 1. 2. k = 2 , = -t 1 for all t and (1. 4) (1. 5) which only depends on t 2 -t 1 (time difference) 5

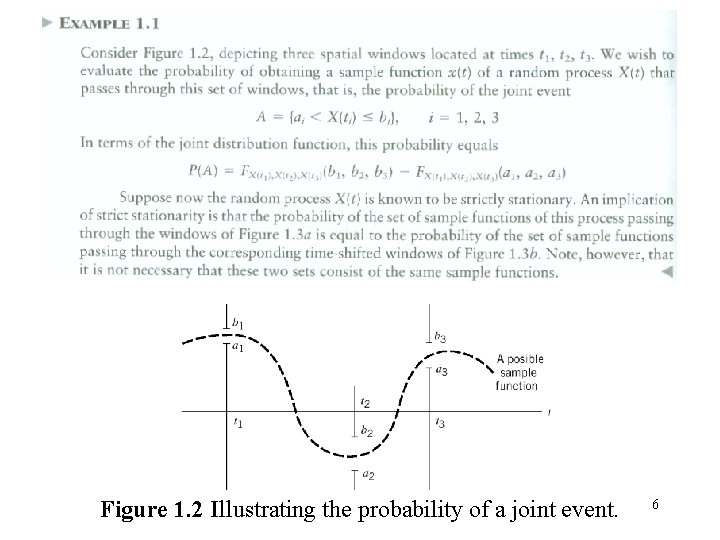
Figure 1. 2 Illustrating the probability of a joint event. 6

Figure 1. 3 Illustrating the concept of stationarity in Example 1. 1. 7

1. 4 Mean, Correlation, and Covariance Function Let X(t) be a strictly stationary RP The mean of X(t) is for all t (1. 6) (1. 7) for all t 1 and t 2 (1. 8) f. X(t)(x) : the first order pdf. The autocorrelation function of X(t) is 8

The autocovariance function (1. 10) Which is of function of time difference (t 2 -t 1). We can determine CX(t 1, t 2) if m. X and RX(t 2 -t 1) are known. Note that: 1. m. X and RX(t 2 -t 1) only provide a partial description. 2. If m. X(t) = m. X and RX(t 1, t 2)=RX(t 2 -t 1), then X(t) is wide-sense stationary (stationary process). 3. The class of strictly stationary processes with finite second-order moments is a subclass of the class of all stationary processes. 4. The first- and second-order moments may not exist. 9

Properties of the autocorrelation function For convenience of notation , we redefine 1. The mean-square value 2. 3. 10

Proof of property 3: 11

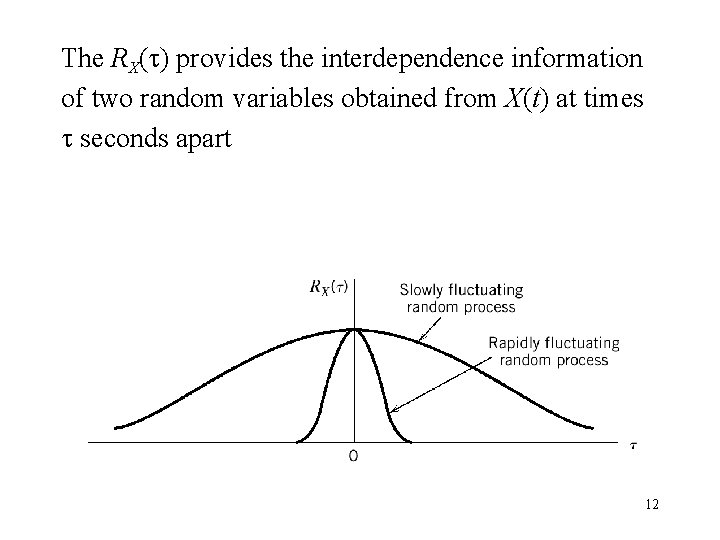
The RX( ) provides the interdependence information of two random variables obtained from X(t) at times seconds apart 12

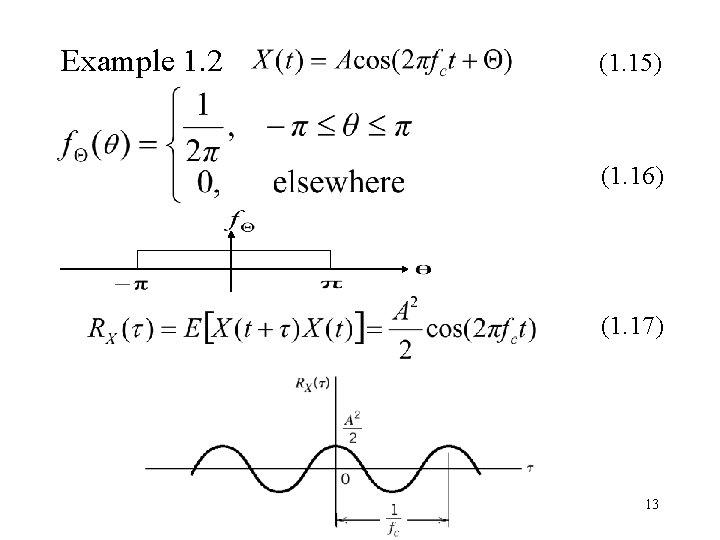
Example 1. 2 (1. 15) (1. 16) (1. 17) 13

Appendix 2. 1 Fourier Transform 14

We refer to |G(f)| as the magnitude spectrum of the signal g(t), and refer to arg {G(f)} as its phase spectrum. 15

DIRAC DELTA FUNCTION Strictly speaking, theory of the Fourier transform is applicable only to time functions that satisfy the Dirichlet conditions. Such functions include energy signals. However, it would be highly desirable to extend this theory in two ways: 1. To combine the Fourier series and Fourier transform into a unified theory, so that the Fourier series may be treated as a special case of the Fourier transform. 2. To include power signals (i. e. , signals for which the average power is finite) in the list of signals to which we may apply the Fourier transform. 16

The Dirac delta function or just delta function, denoted by , is defined as having zero amplitude everywhere except at , where it is infinitely large in such a way that it contains unit area under its curve; that is (A 2. 3) and (A 2. 4) (A 2. 5) (A 2. 6) 17

18

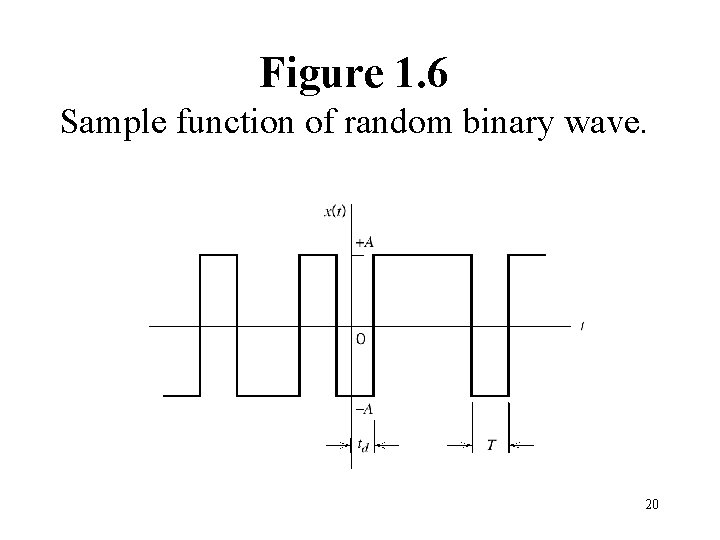
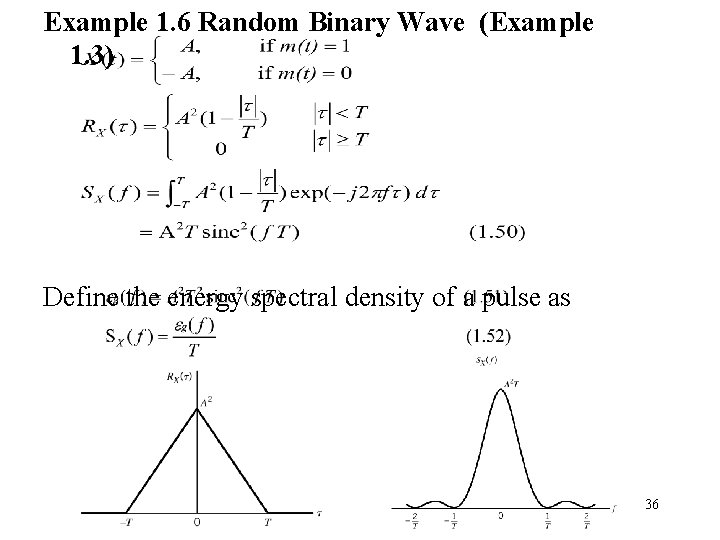
Example 1. 3 Random Binary Wave / Pulse 1. The pulses are represented by ±A volts (mean=0). 2. The first complete pulse starts at td. 3. During , the presence of +A or –A is random. 4. When , Tk and Ti are not in the same pulse interval, hence, X(tk) and X(ti) are independent. 19

Figure 1. 6 Sample function of random binary wave. 20

4. When , Tk and Ti are not in the same pulse interval, hence, X(tk) and X(ti) are independent. 21
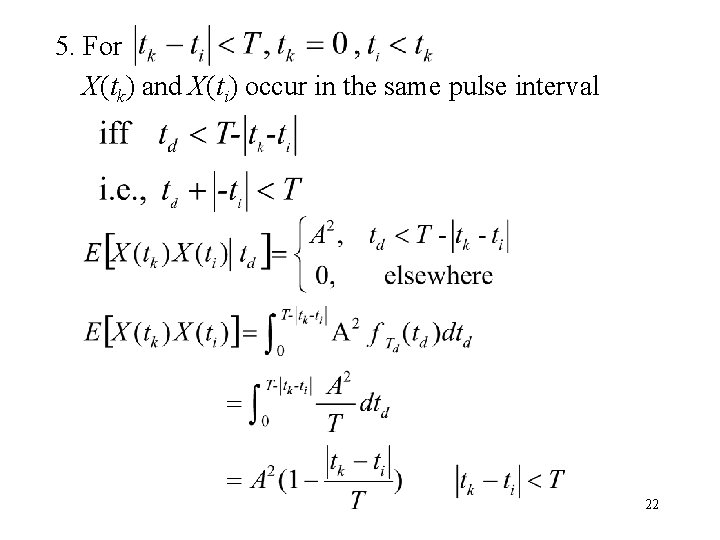
5. For X(tk) and X(ti) occur in the same pulse interval 22

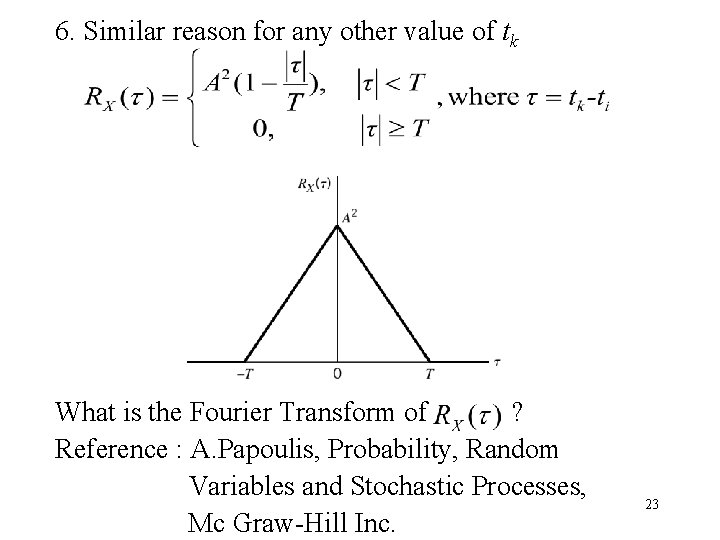
6. Similar reason for any other value of tk What is the Fourier Transform of ? Reference : A. Papoulis, Probability, Random Variables and Stochastic Processes, Mc Graw-Hill Inc. 23

Cross-correlation Function and Note and functions. The correlation matrix is are not general even If X(t) and Y(t) are jointly stationary 24
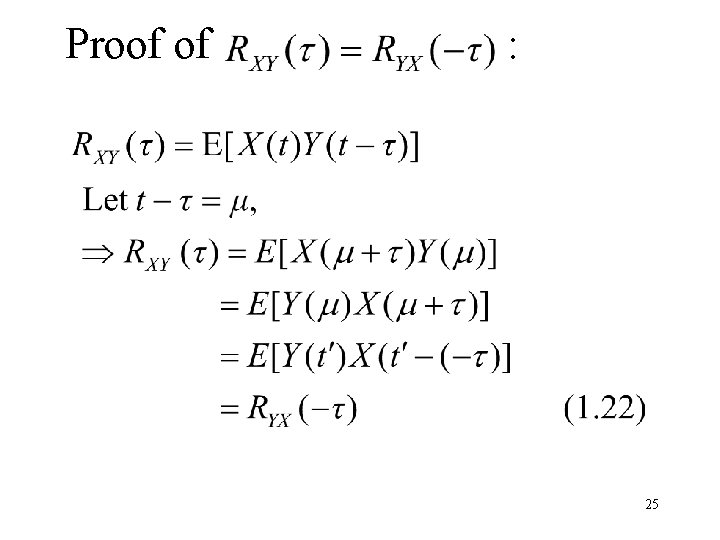
Proof of : 25

Example 1. 4 Quadrature-Modulated Process where X(t) is a stationary process and is uniformly distributed over [0, 2 ]. =0 26

1. 5 Ergodic Processes Ensemble averages of X(t) are averages “across the process”. Long-term averages (time averages) are averages “along the process ” DC value of X(t) (random variable) If X(t) is stationary, 27

represents an unbiased estimate of The process X(t) is ergodic in the mean, if The time-averaged autocorrelation function If the following conditions hold, X(t) is ergodic in the autocorrelation functions 28

1. 6 Transmission of a random Process Through a Linear Time-Invariant Filter (System) where h(t) is the impulse response of the system If E[X(t)] is finite and system is stable If X(t) is stationary, H(0) : System DC response. 29

Consider autocorrelation function of Y(t): If is finite and the system is stable, If (stationary) Stationary input, Stationary output 30

1. 7 Power Spectral Density (PSD) Consider the Fourier transform of g(t), Let H(f ) denote the frequency response, 31

: the magnitude response Define: Power Spectral Density ( Fourier Transform of Recall Let ) be the magnitude response of an ideal narrowband filter (1. 40) D f : Filter Bandwidth 32

Properties of The PSD Einstein-Wiener-Khintahine relations: is more useful than ! 33

34

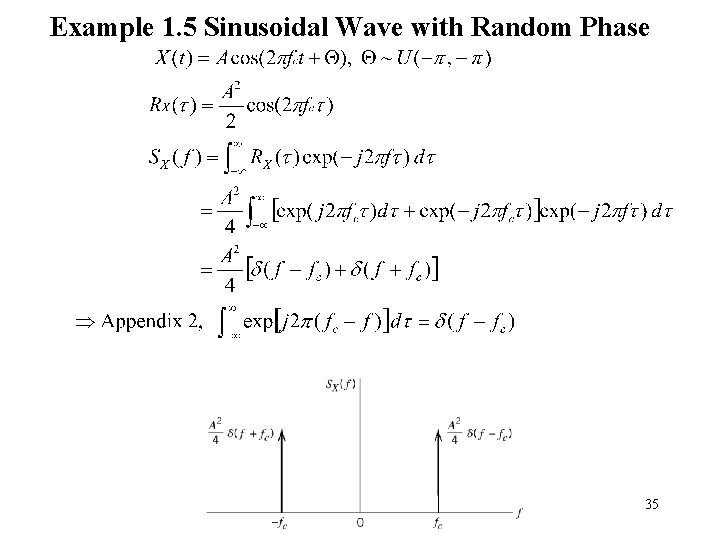
Example 1. 5 Sinusoidal Wave with Random Phase 35

Example 1. 6 Random Binary Wave (Example 1. 3) Define the energy spectral density of a pulse as 36

Example 1. 7 Mixing of a Random Process with a Sinusoidal Process We shift the to the right by add them and divide by 4. , shift it to the left by , 37

Relation Among The PSD of The Input and Output Random Processes X(t) SX (f) h(t) Y(t) SY (f) Recall (1. 32) 38

Relation Among The PSD and The Magnitude Spectrum of a Sample Function Let x(t) be a sample function of a stationary and ergodic Process X(t). In general, the condition for Fourier transformable is This condition can never be satisfied by any stationary x(t) with infinite duration. We may write If x(t) is a power signal (finite average power) Time-averaged autocorrelation periodogram function 39

Take inverse Fourier Transform of right side of (1. 62) From (1. 61), (1. 63), we have Note that for any given x(t) periodogram does not converge as Since x(t) is ergodic (1. 67) is used to estimate the PSD of x(t) 40

Cross-Spectral Densities 41

Example 1. 8 X(t) and Y(t) are zero mean stationary processes. Consider Example 1. 9 X(t) and Y(t) are jointly stationary. 42

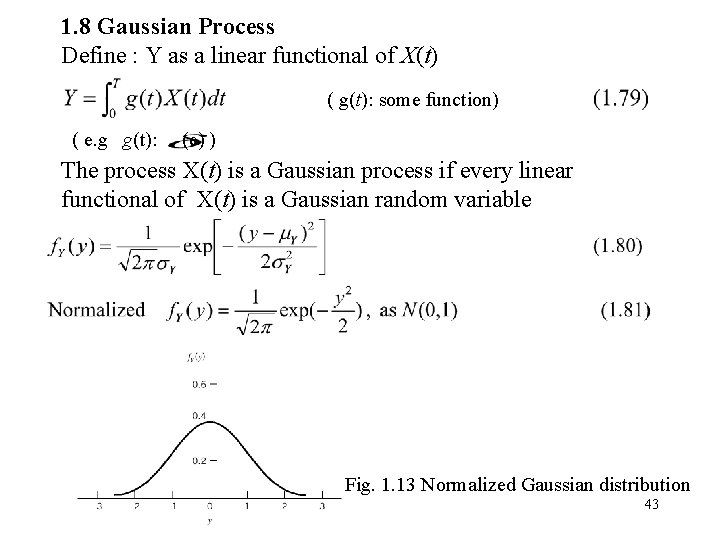
1. 8 Gaussian Process Define : Y as a linear functional of X(t) ( g(t): some function) ( e. g g(t): (e) ) The process X(t) is a Gaussian process if every linear functional of X(t) is a Gaussian random variable Fig. 1. 13 Normalized Gaussian distribution 43

Central Limit Theorem Let Xi , i =1, 2, 3, …. N be (a) statistically independent R. V. and (b) have mean and variance. Since they are independently and identically distributed (i. i. d. ) Normalized Xi The Central Limit Theorem The probability distribution of VN approaches N(0, 1) as N approaches infinity. 44

Properties of A Gaussian Process 1. X(t) Gaussian h(t) Y(t) Gaussian 45

2. If X(t) is Gaussisan Then X(t 1) , X(t 2) , X(t 3) , …. , X(tn) are jointly Gaussian. Let and the set of covariance functions be 46

3. If a Gaussian process is stationary then it is strictly stationary. (This follows from Property 2) 4. If X(t 1), X(t 2), …. . , X(tn) are uncorrelated as Then they are independent Proof : uncorrelated is also a diagonal matrix (1. 85) 47

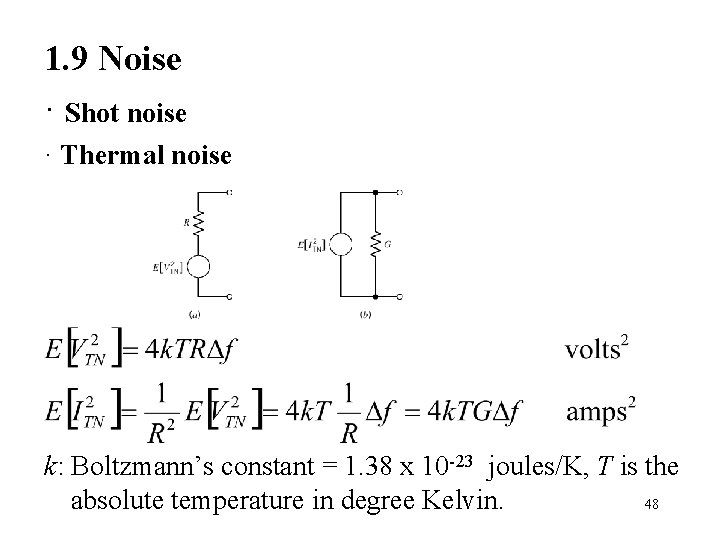
1. 9 Noise · Shot noise · Thermal noise k: Boltzmann’s constant = 1. 38 x 10 -23 joules/K, T is the absolute temperature in degree Kelvin. 48

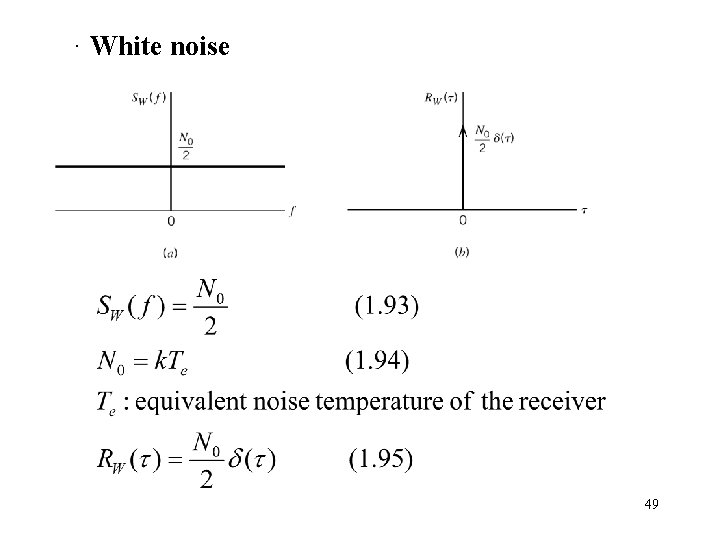
· White noise 49

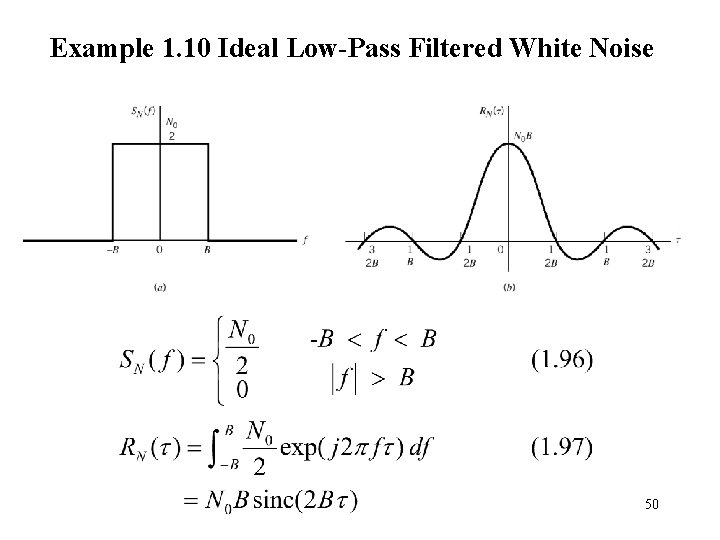
Example 1. 10 Ideal Low-Pass Filtered White Noise 50

Example 1. 11 Correlation of White Noise with a Sinusoidal Wave White noise X 51

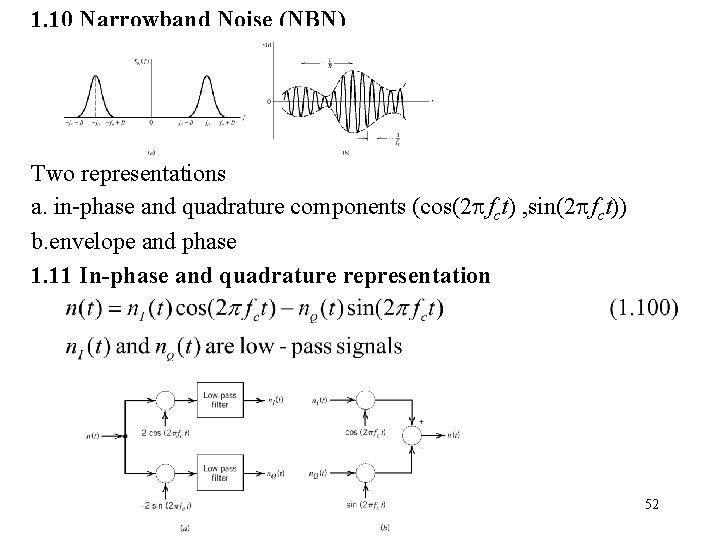
1. 10 Narrowband Noise (NBN) Two representations a. in-phase and quadrature components (cos(2 fct) , sin(2 fct)) b. envelope and phase 1. 11 In-phase and quadrature representation 52

Important Properties 1. n. I(t) and n. Q(t) have zero mean. 2. If n(t) is Gaussian then n. I(t) and n. Q(t) are jointly Gaussian. 3. If n(t) is stationary then n. I(t) and n. Q(t) are jointly stationary. 4. 5. n. I(t) and n. Q(t) have the same variance. 6. Cross-spectral density is purely imaginary. 7. If n(t) is Gaussian, its PSD is symmetric about fc, then n. I(t) and n. Q(t) are statistically independent. 53

Example 1. 12 Ideal Band-Pass Filtered White Noise 54

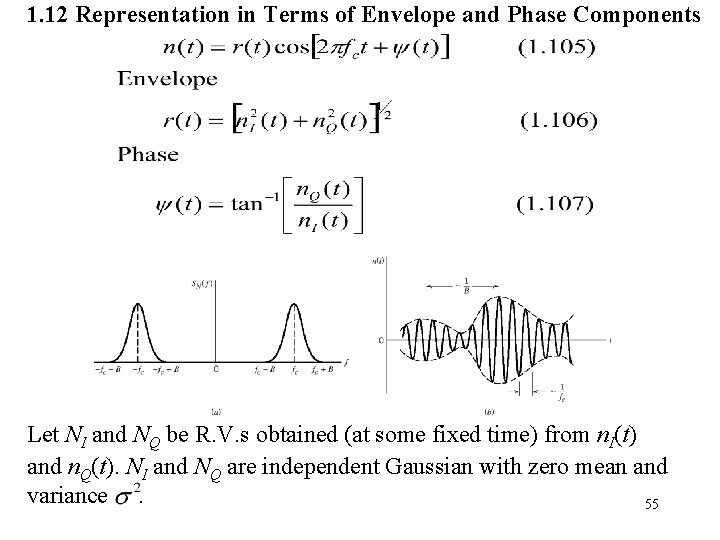
1. 12 Representation in Terms of Envelope and Phase Components Let NI and NQ be R. V. s obtained (at some fixed time) from n. I(t) and n. Q(t). NI and NQ are independent Gaussian with zero mean and variance. 55

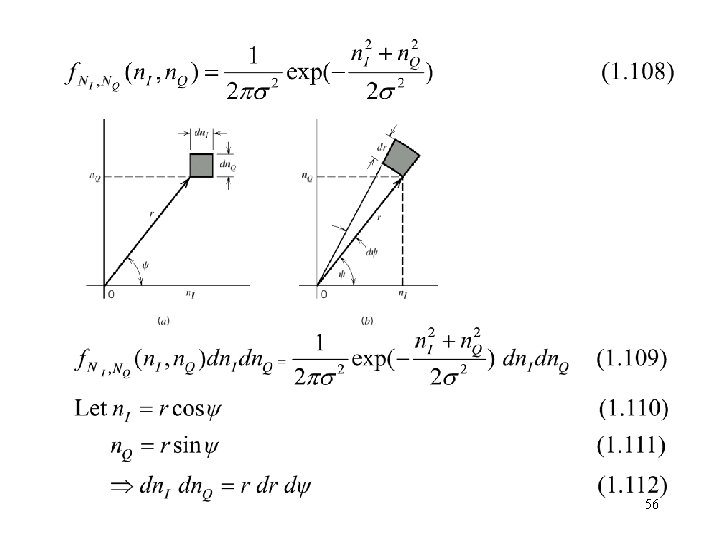
56

Substituting (1. 110) - (1. 112) into (1. 109) 57

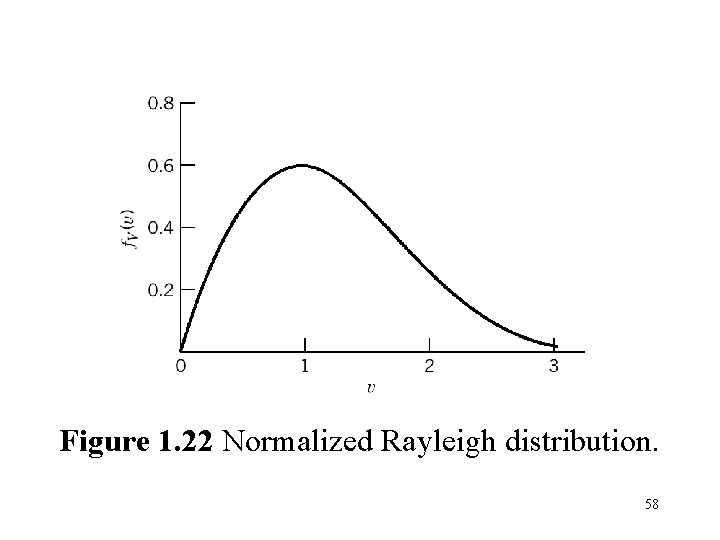
Figure 1. 22 Normalized Rayleigh distribution. 58

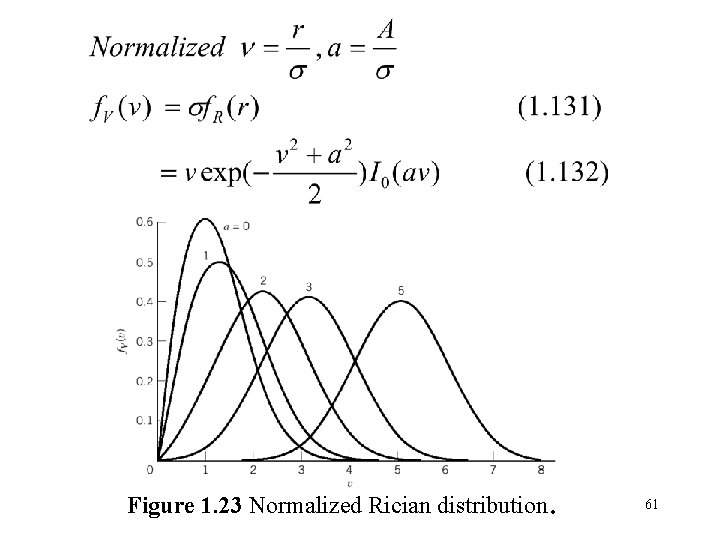
1. 13 Sine Wave Plus Narrowband Noise If n(t) is Gaussian with zero mean and variance 1. and are Gaussian and statistically independent. 2. The mean of is A and that of is zero. 3. The variance of and is. 59

The modified Bessel function of the first kind of zero order is defined is (Appendix 3) It is called Rician distribution. 60

Figure 1. 23 Normalized Rician distribution . 61
 Ergodic process in random process
Ergodic process in random process Random assignment vs random sampling
Random assignment vs random sampling Random assignment vs random selection
Random assignment vs random selection Random process
Random process Stochastic process
Stochastic process Jointly stationary and ergodic process
Jointly stationary and ergodic process Bandpass random process
Bandpass random process Chapter 16 random variables
Chapter 16 random variables Chapter 15 random variables
Chapter 15 random variables Chapter 15 random variables
Chapter 15 random variables The pricing tripod
The pricing tripod Physical fitness components and tests grade 9
Physical fitness components and tests grade 9 Physical features of india introduction
Physical features of india introduction Physical education introduction
Physical education introduction Physical examination introduction
Physical examination introduction Perfume evaporating chemical or physical
Perfume evaporating chemical or physical Caput succedaneum vs cephalohematoma
Caput succedaneum vs cephalohematoma Body paragraph
Body paragraph Introduction of business process
Introduction of business process Stochastic process introduction
Stochastic process introduction List of manufacturing processes
List of manufacturing processes Business process automation ppt
Business process automation ppt Curriculum wing in pakistan
Curriculum wing in pakistan Introduction to process control
Introduction to process control Objective of sand casting
Objective of sand casting Lvn vs lpn
Lvn vs lpn Nursing care plan hallucinations
Nursing care plan hallucinations Introduction to the personal software process
Introduction to the personal software process New product introduction process
New product introduction process Olecranon process vs fossa
Olecranon process vs fossa Substantive vs procedural due process
Substantive vs procedural due process Business process levels
Business process levels What is process to process delivery
What is process to process delivery Coronoid and condylar process
Coronoid and condylar process Stable quality
Stable quality Process-to-process delivery
Process-to-process delivery Sweet process review
Sweet process review Summative and subjective assessment
Summative and subjective assessment Physics chapter 2 review answers
Physics chapter 2 review answers Chapter 6 physical science
Chapter 6 physical science A 120m long ski lift carries skiers
A 120m long ski lift carries skiers Chapter 15 physical oceanography
Chapter 15 physical oceanography Chapter 15 physical oceanography
Chapter 15 physical oceanography Chapter 17 physical science
Chapter 17 physical science Chapter 15 review physical science
Chapter 15 review physical science Chapter 4 physical activity for life answers
Chapter 4 physical activity for life answers General physical exam
General physical exam Chapter 27 physical geography of east asia
Chapter 27 physical geography of east asia Chapter 22 physical distribution
Chapter 22 physical distribution Chapter 15 physical oceanography
Chapter 15 physical oceanography Russia and the eurasian republics physical map
Russia and the eurasian republics physical map Lesson 1 physical geography of southeast asia
Lesson 1 physical geography of southeast asia Definition of eastern europe
Definition of eastern europe Chapter 12 lesson 1 benefits of physical activity
Chapter 12 lesson 1 benefits of physical activity Chapter 12 lesson 1 answer key
Chapter 12 lesson 1 answer key Physical education chapter 1
Physical education chapter 1 Chapter 10 physical development from one to three
Chapter 10 physical development from one to three Chapter 4 review physical science
Chapter 4 review physical science Chapter 11 physical science
Chapter 11 physical science Chapter 14 review physical science
Chapter 14 review physical science Conceptual physical science practice sheet chapter 2
Conceptual physical science practice sheet chapter 2 Copyright
Copyright