Chapter 1 Preliminaries Copyright 2005 Pearson Education Inc

Chapter 1 Preliminaries Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

1. 3 Functions and Their Graphs (1 st lecture of week 06/08/07 11/08/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

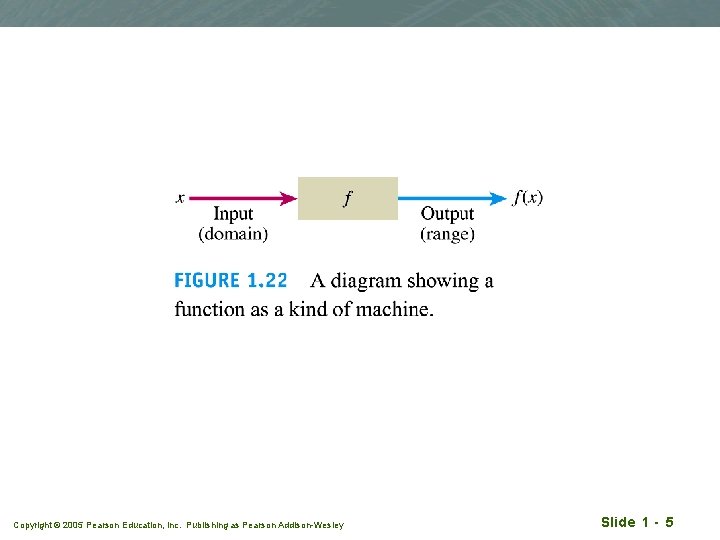
Function qy = f(x) q f represents function (a rule that tell us how to calculate the value of y from the variable x q x : independent variable (input of f ) q y : dependent variable (the correspoinding output value of f at x) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 3

Definition Domain of the function The set of D of all possible input values Definition Range of the function The set of all values of f(x) as x varies throughout D Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 4

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 5

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 6

Natural Domain q When a function y = f(x)is defined and the domain is not stated explicitly, the domain is assumed to be the largest set of real xvalues for the formula gives real y-values. q e. g. compare “y = x 2” c. f. “y = x 2, x≥ 0” q Domain may be open, closed, half open, finite, infinite. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 7

Verify the domains and ranges of these functions Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 8

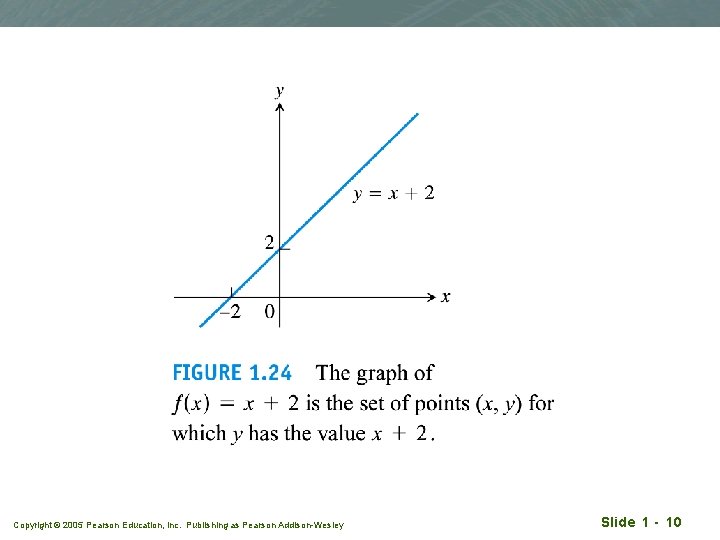
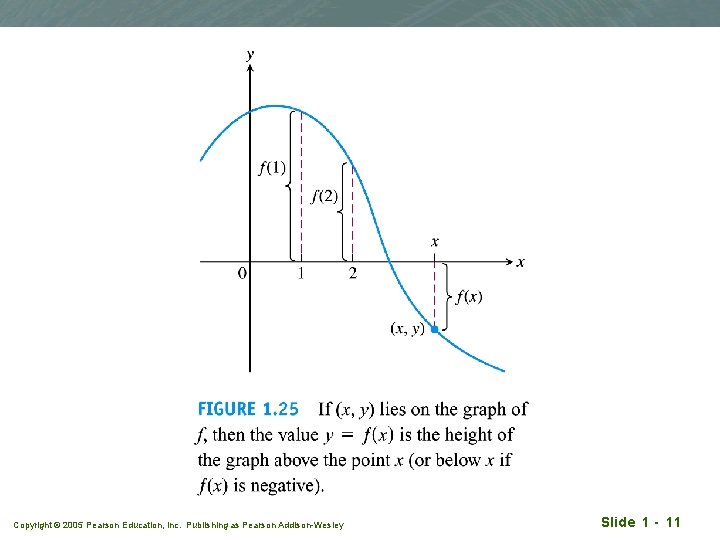
Graphs of functions q Graphs provide another way to visualise a function q In set notation, a graph is {(x, f(x)) | x D} q The graph of a function is a useful picture of its behaviour. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 9

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 10

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 11

Example 2 Sketching a graph q Graph the function y = x 2 over the interval [-2, 2] Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 12

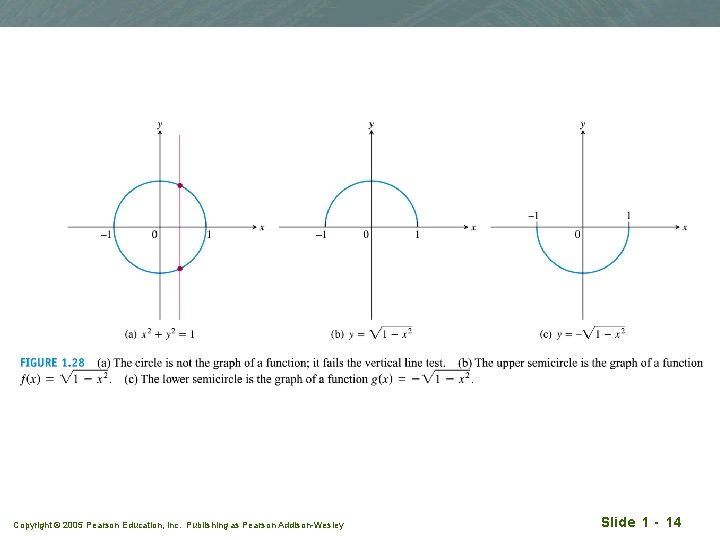
The vertical line test q Since a function must be single valued over its domain, no vertical line can intersect the graph of a function more than once. q If a is a point in the domain of a function f, the vertical line x=a can intersect the graph of f in a single point (a, f(a)). Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 13

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 14

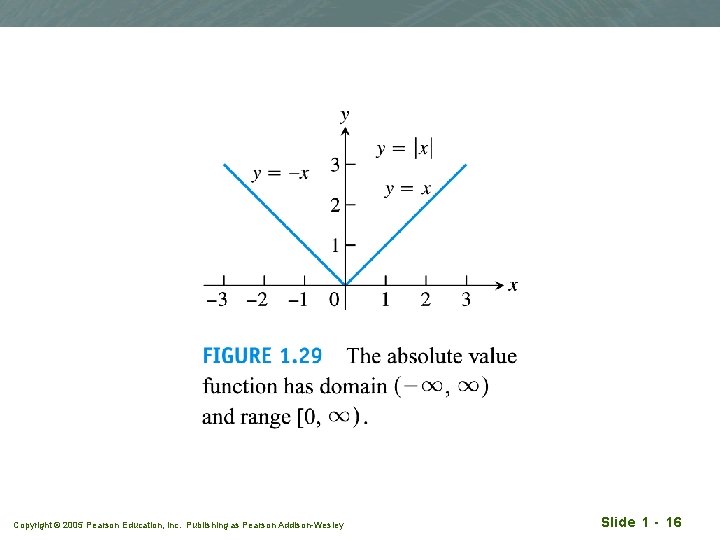
Piecewise-defined functions q The absolute value function Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 15

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 16

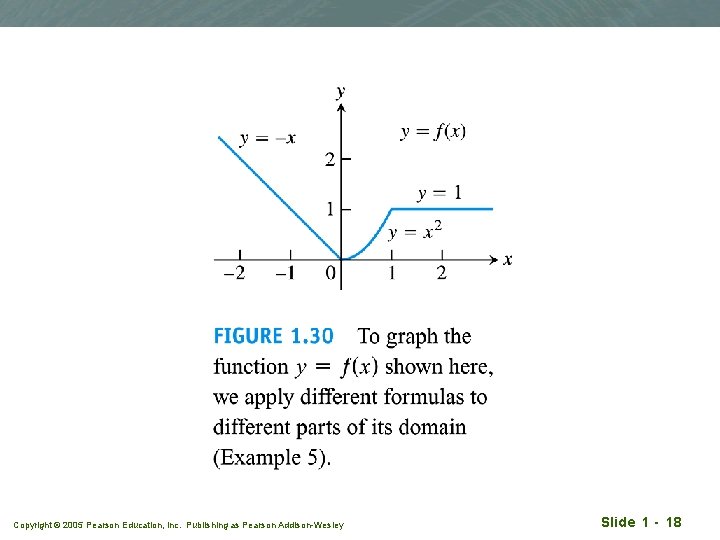
Graphing piecewise-defined functions q Note: this is just one function with a domain covering all real number Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 17

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 18

The greatest integer function q Also called integer floor function q f = [x], defined as greatest integer less than or equal to x. q e. g. q [2. 4] = 2 q [2]=2 q [-2] = -2, etc. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 19

Note: the graph is the blue colour lines, not the one in red Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 20

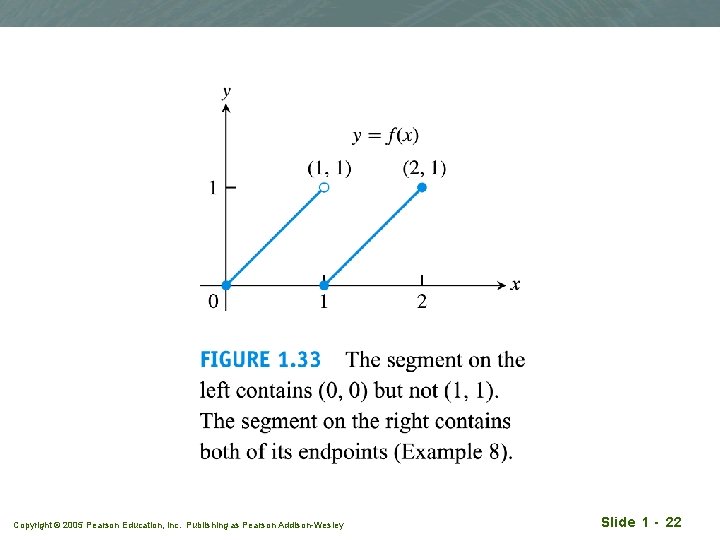
Writing formulas for piecewise-defined functions q Write a formula for the function y=f(x) in Figure 1. 33 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 21

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 22

1. 4 Identifying Functions; Mathematical Models (1 st lecture of week 06/08/07 - 11/08/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

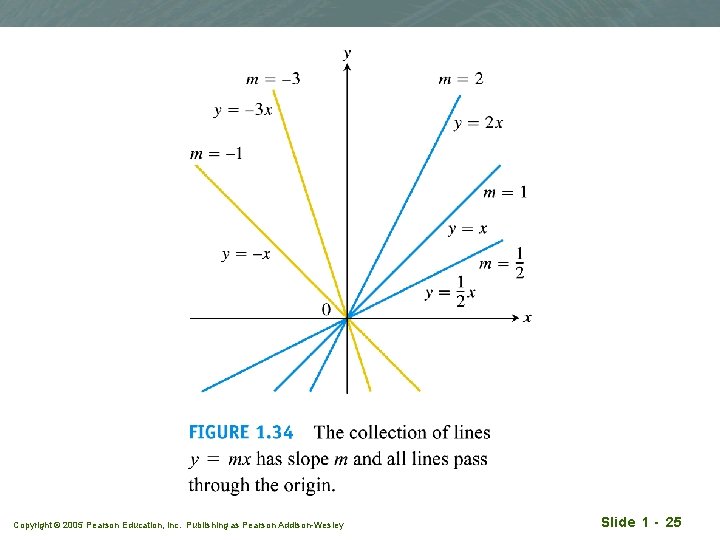
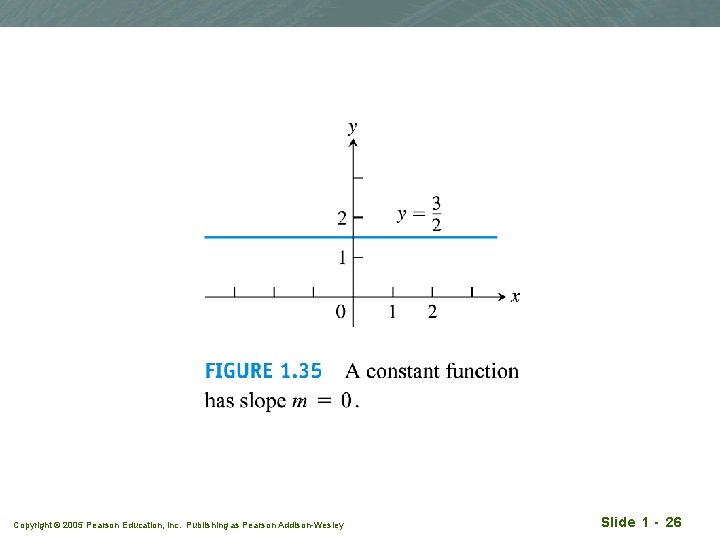
Linear functions q Linear function takes the form of q y=mx + b q m, b constants q m slope of the graph q b intersection with the y-axis q The linear function reduces to a constant function f = c when m = 0, Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 24

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 25

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 26

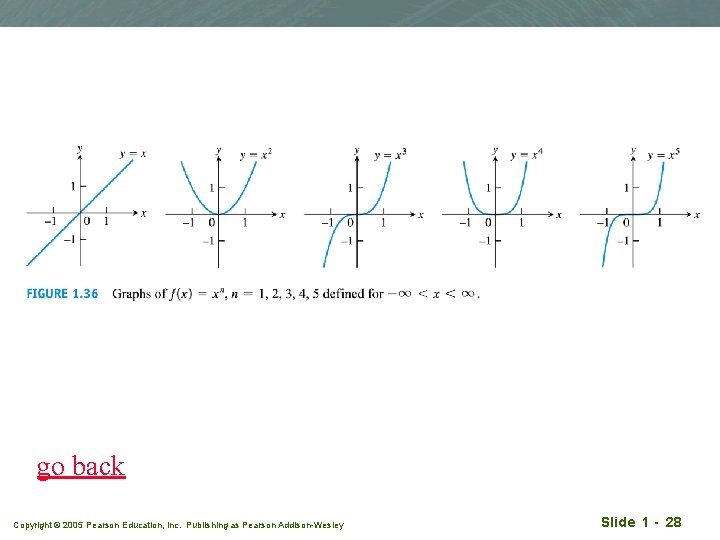
Power functions q f(x) = xa q a constant q Case (a): a = n, a positive integer Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 27

go back Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 28

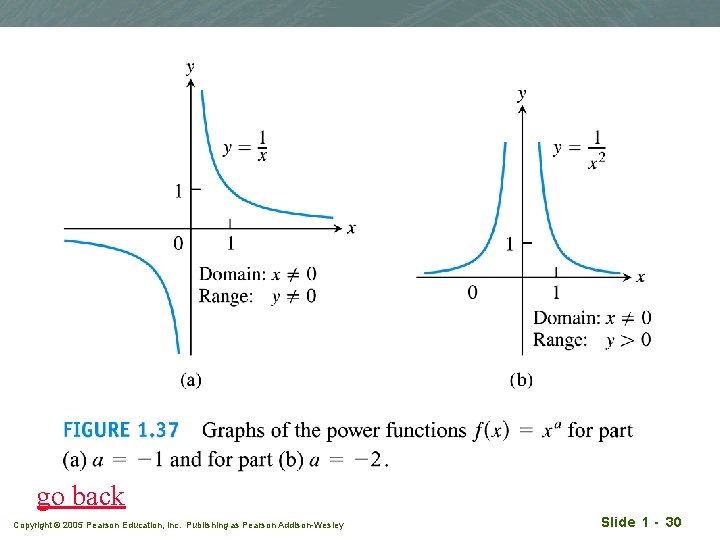
Power functions q Case (b): q a = -1 (hyperbola) q or a=-2 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 29

go back Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 30

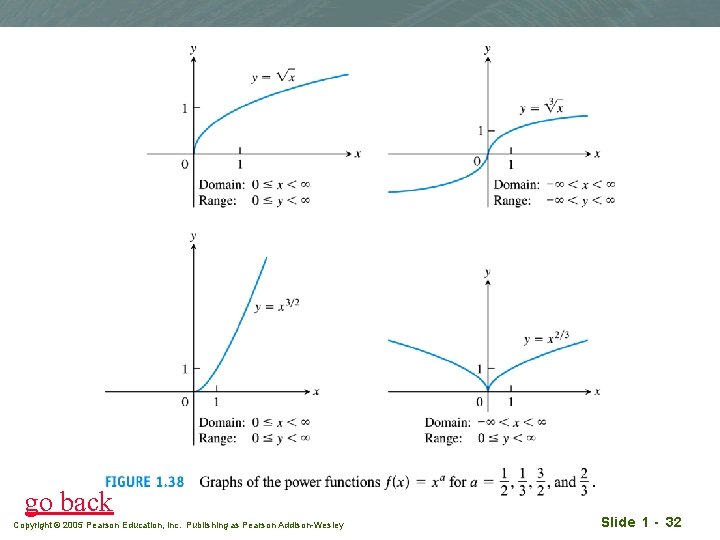
Power functions q q q Case (c): a = ½, 1/3, 3/2, and 2/3 f(x) = x½ = x (square root) , domain = [0 ≤ x < ∞) g(x) = x 1/3 = 3 x(cube root), domain = (-∞ < x < ∞) p(x) = x 2/3= (x 1/3)2, domain = ? q(x) = x 3/2= (x 3)1/2 domain = ? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 31

go back Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 32

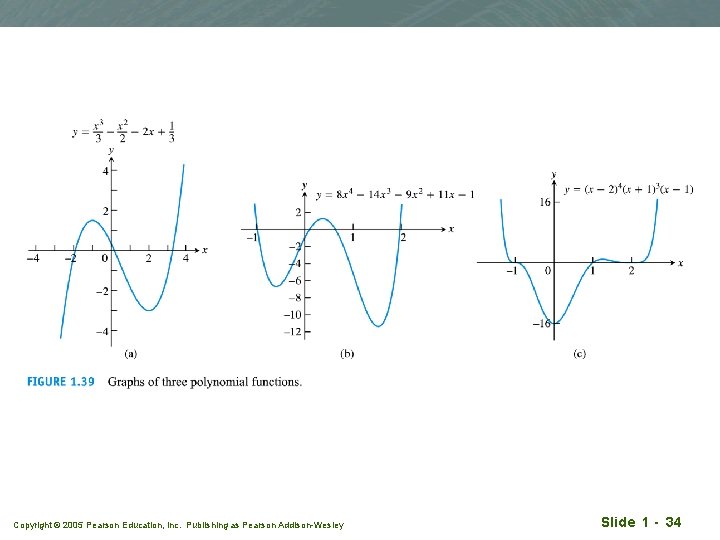
Polynomials anxn + an-1 xn-1 + an-2 xn-2 + a 1 x + a 0 q n nonnegative integer (1, 2, 3…) q a’s coefficients (real constants) q If an 0, n is called the degree of the polynomial q p(x)= Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 33

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 34

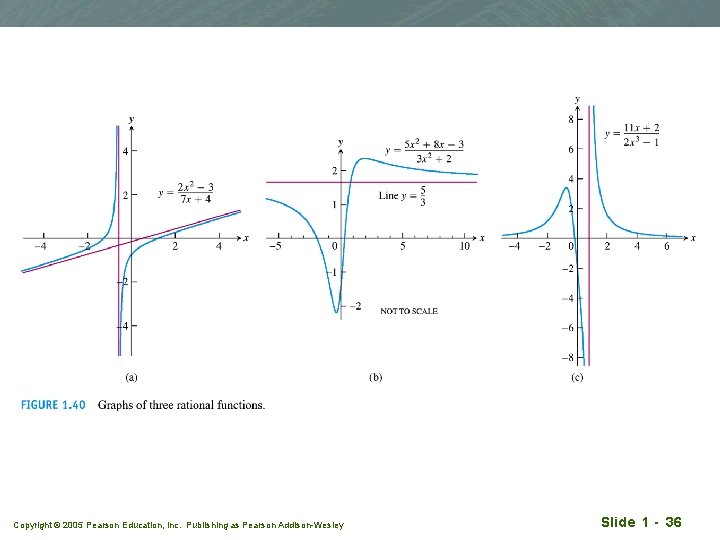
Rational functions q. A rational function is a quotient of two polynomials: q f(x) = p(x) / q(x) q p, q are polynomials. q Domain of f(x) is the set of all real number x for which q(x) 0. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 35

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 36

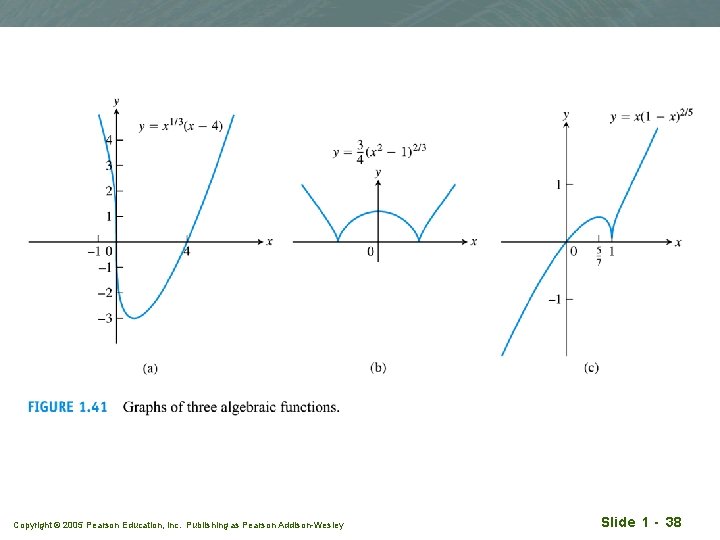
Algebraic functions q Functions constructed from polynomials using algebraic operations (addition, subtraction, multiplication, division, and taking roots) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 37

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 38

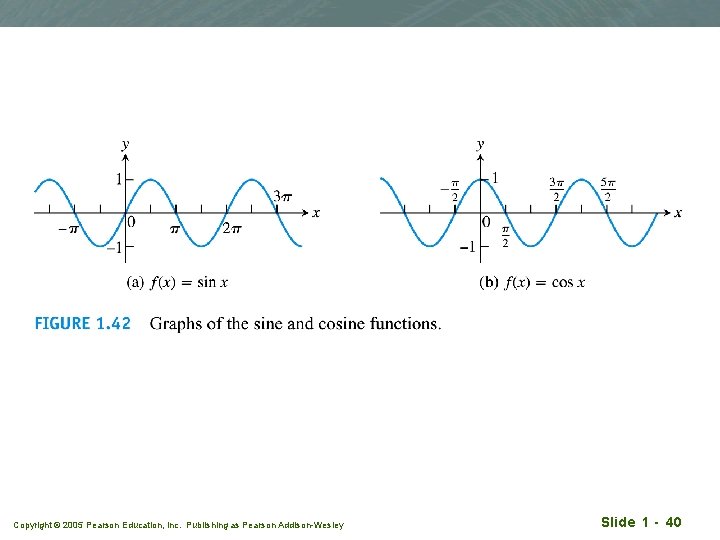
Trigonometric functions q More details in later chapter Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 39

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 40

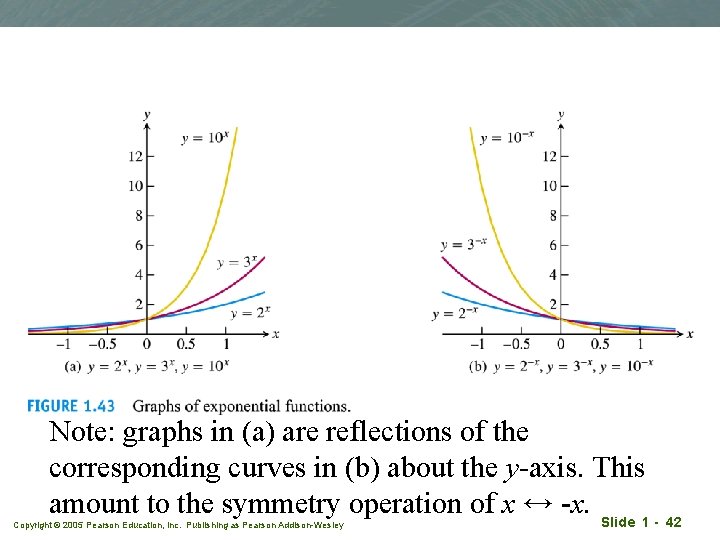
Exponential functions q f(x) = ax q Where a > 0 and a 0. a is called the ‘base’. q Domain (-∞, ∞) q Range (0, ∞) q Hence, f(x) > 0 q More in later chapter Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 41

Note: graphs in (a) are reflections of the corresponding curves in (b) about the y-axis. This amount to the symmetry operation of x ↔ -x. Slide 1 - 42 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

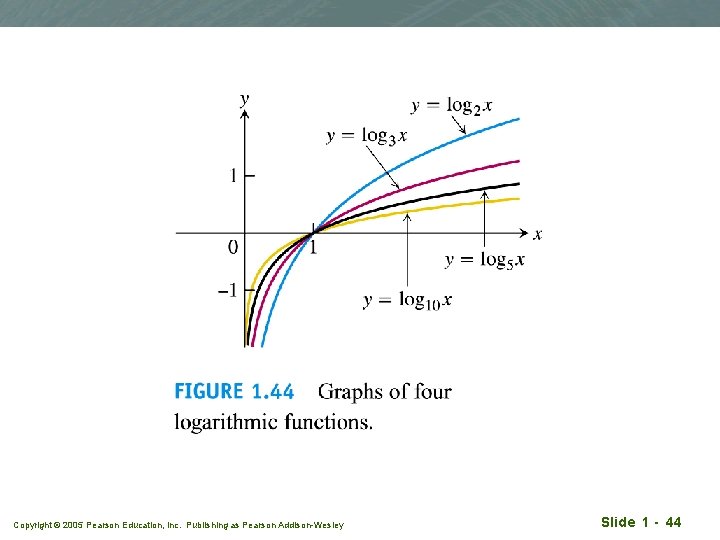
Logarithmic functions q f(x) = loga x q a is the base q a 1, a >0 q Domain (0, ∞) q Range (-∞, ∞) q They are the inverse functions of the exponential functions (more in later chapter) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 43

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 44

Transcendental functions q Functions that are not algebraic q Include: trigonometric, inverse trigonometric, exponential, logarithmic, hyperbolic and many other functions Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 45

Example 1 q Recognizing Functions q (a) f(x) = 1 + x – ½x 5 q (b) g(x) = 7 x q (c) h(z) = z 7 q (d) y(t) = sin(t–p/4) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 46

Increasing versus decreasing functions q. A function is said to be increasing if it rises as you move from left to right q A function is said to be decreasing if it falls as you move from left to right Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 47

y=x 2, y=x 3; y=1/x, y=1/x 2; y=x 1/2, y=x 2/3 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 48

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 49

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 50

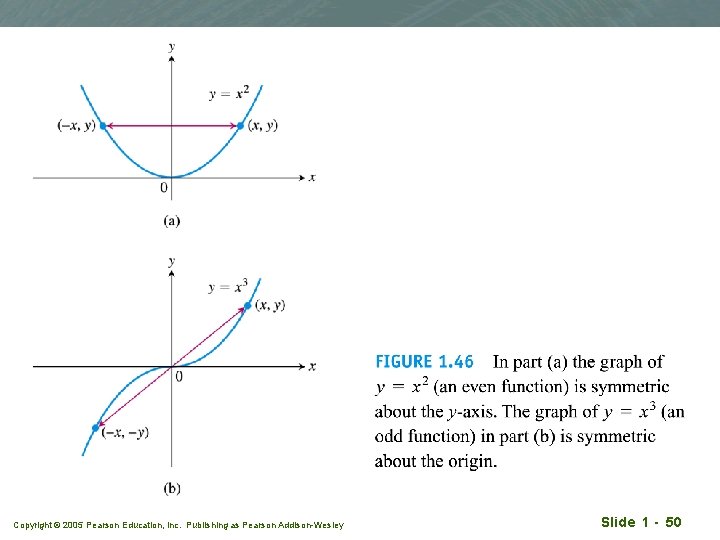
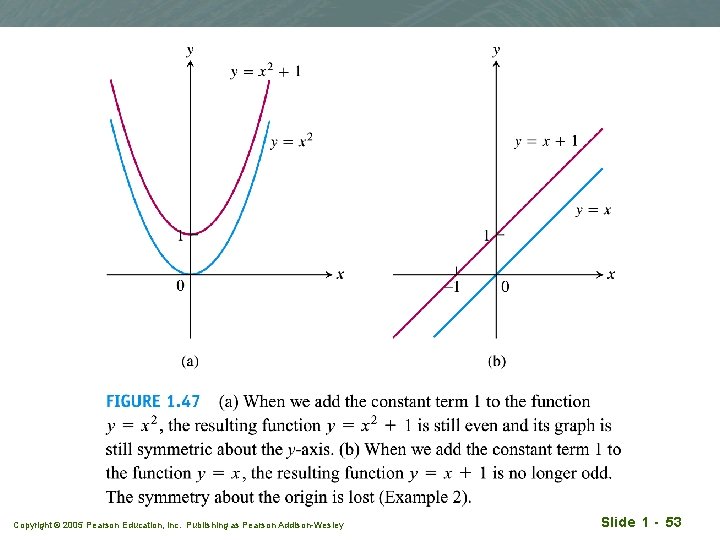
Recognising even and odd functions q f(x) = x 2 Even function as (-x)2 = x 2 for all x, symmetric about the y-axis. q f(x) = x 2 + 1 Even function as (-x)2 + 1 = x 2+ 1 for all x, symmetric about the y-axis. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 51

Recognising even and odd functions q f(x) = x. Odd function as (-x) = -x for all x, symmetric about origin. q f(x) = x+1. Odd function ? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 52

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 53

1. 5 Combining Functions; Shifting and Scaling Graphs (2 nd lecture of week 06/08/07 - 11/08/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

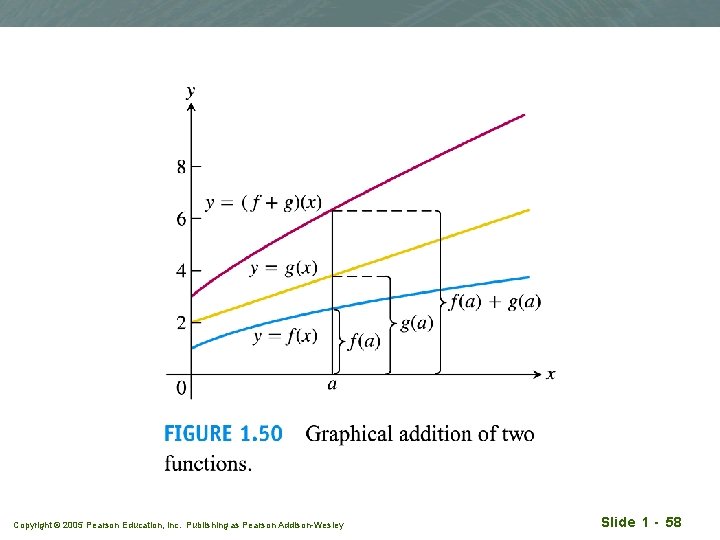
Sums, differences, products and quotients q q q f, g are functions For x D(f )∩D(g), we can define the functions of (f +g) (x) = f(x) + g(x) (f - g) (x) = f(x) - g(x) (fg)(x) = f(x)g(x), (cf)(x) = cf(x), c a real number q Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 55

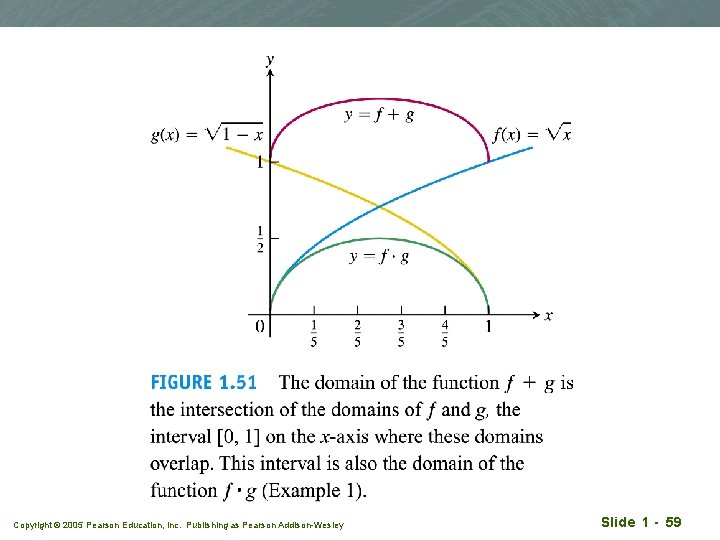
Example 1 = x, g(x) = (1 -x), q The domain common to both f, g is q D(f )∩D(g) = [0, 1] (work it out) q f(x) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 56

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 57

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 58

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 59

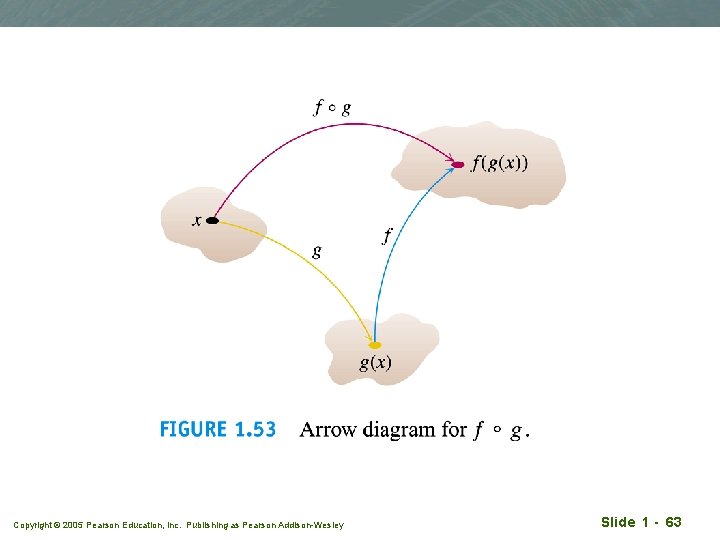
Composite functions q Another way of combining functions Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 60

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 61

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 62

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 63

Example 2 q Viewing a function as a composite q y(x) = (1 – x 2) is a composite of q g(x) = 1 – x 2 and f(x) = x q i. e. y(x) = f [g(x)] = (1 – x 2) q Domain of the composite function is |x|≤ 1, or [-1, 1] q Is f [g(x)] = g [f(x)]? Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 64

Example 3 q Read it yourself q Make sure that you know how to work out the domains and ranges of each composite functions listed Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 65

Shifting a graph of a function Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 66

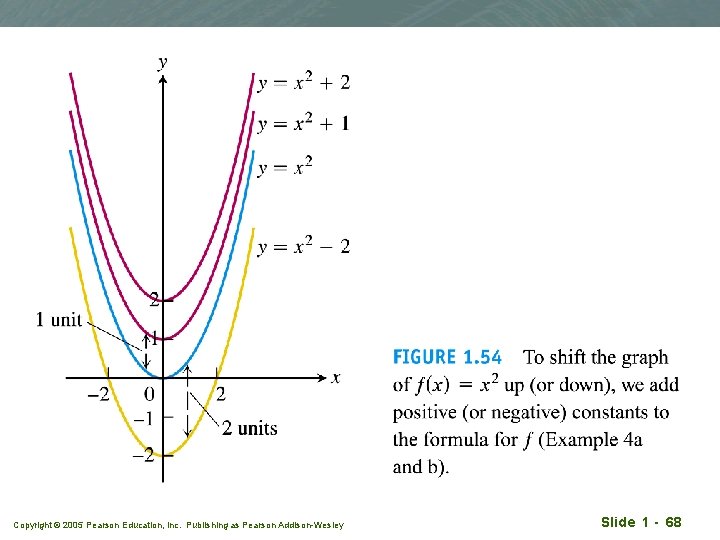
Example 4 q (a) y = x 2, y = x 2 +1 q (b) y = x 2, y = x 2 -2 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 67

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 68

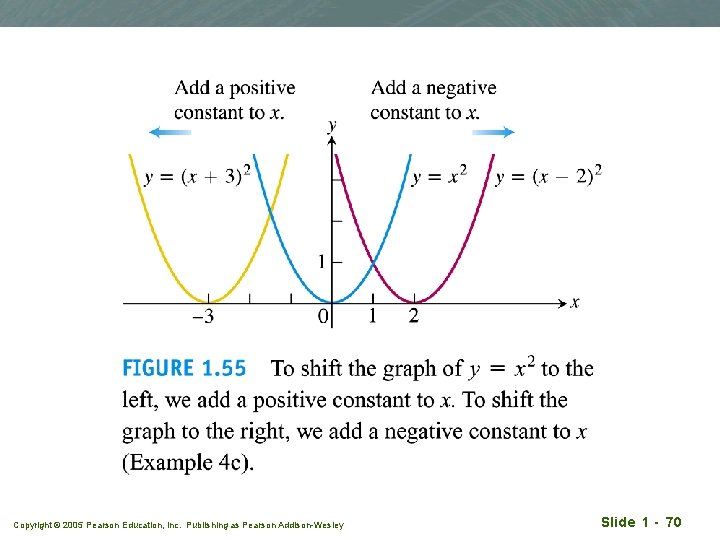
Example 4 q (c) y = x 2, y = (x + 3)2, y = (x - 3)2 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 69

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 70

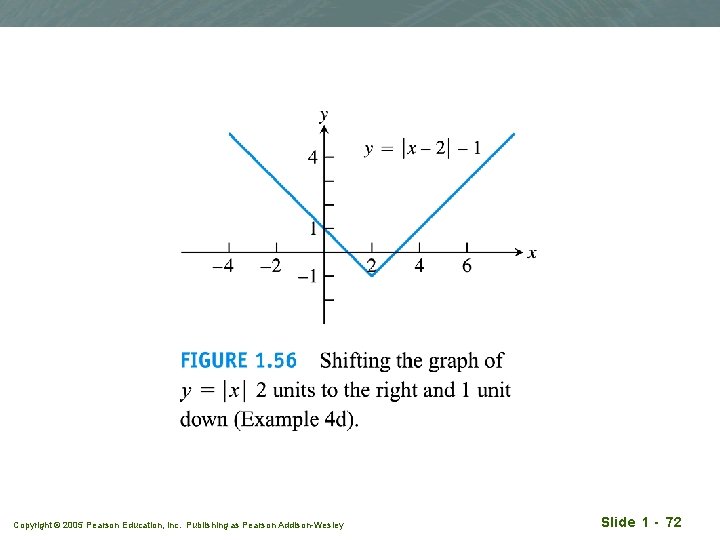
Example 4 q (d) y = |x|, y = |x - 2| - 1 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 71

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 72

Scaling and reflecting a graph of a function q To scale a graph of a function is to stretch or compress it, vertically or horizontally. q This is done by multiplying a constant c to the function or the independent variable Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 73

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 74

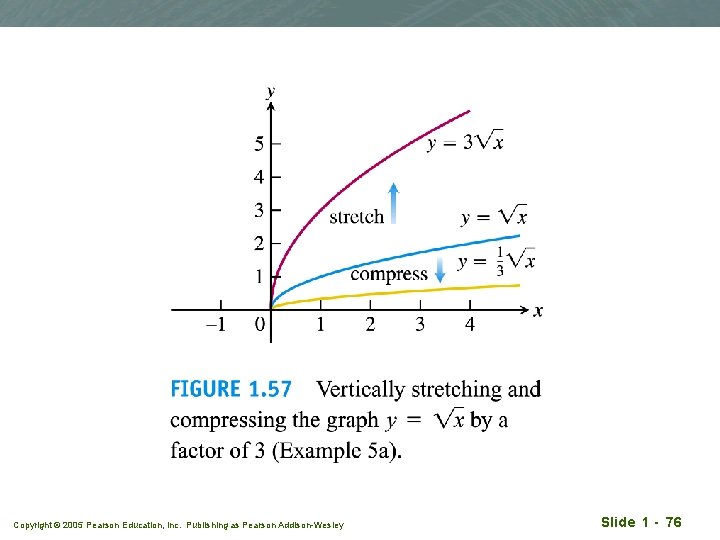
Example 5(a) q Vertical stretching and compression of the graph y = x by a factor or 3 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 75

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 76

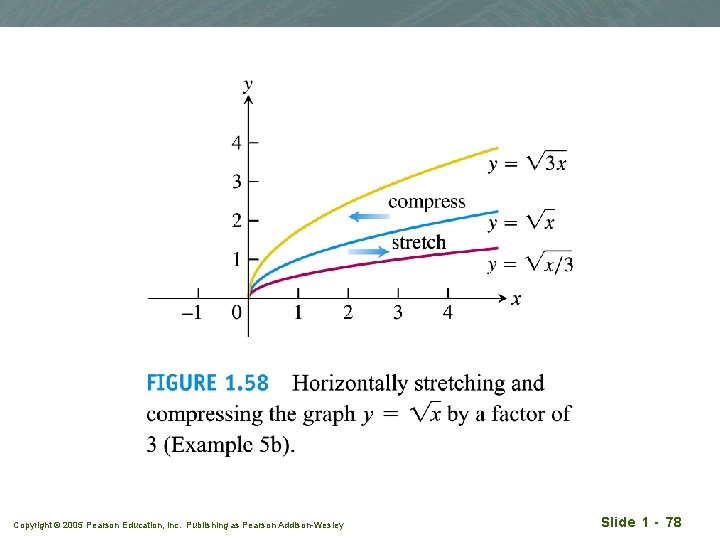
Example 5(b) q Horizontal stretching and compression of the graph y = x by a factor of 3 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 77

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 78

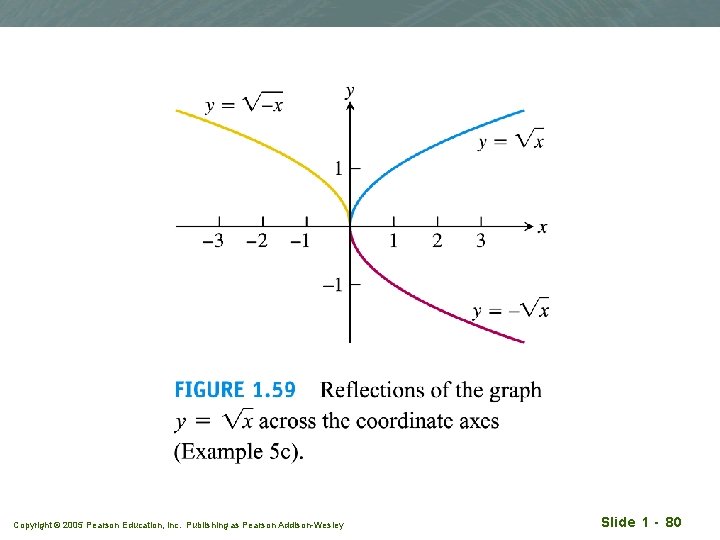
Example 5(c) q Reflection qc across the x- and y- axes = -1 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 79

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 80

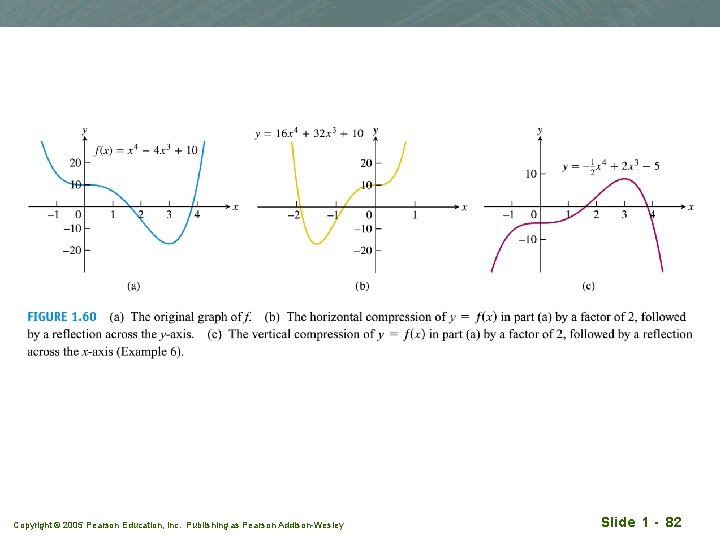
Example 6 q Read it yourself Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 81

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 82

1. 6 Trigonometric Functions (2 nd lecture of week 06/08/07 11/08/07) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

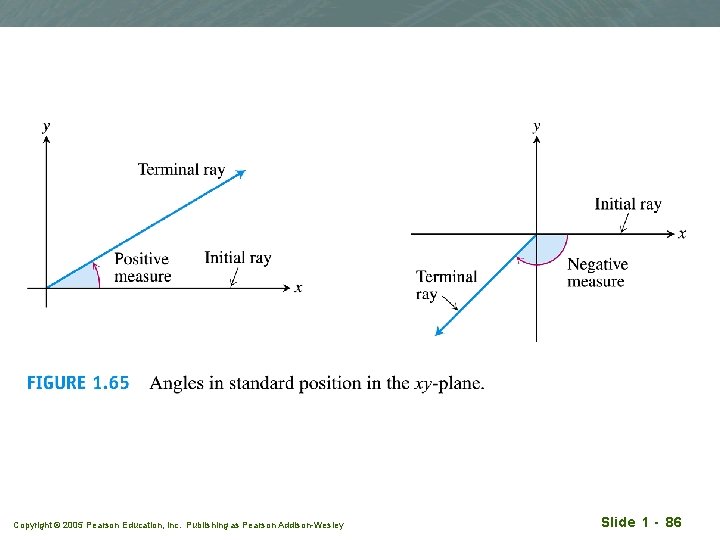
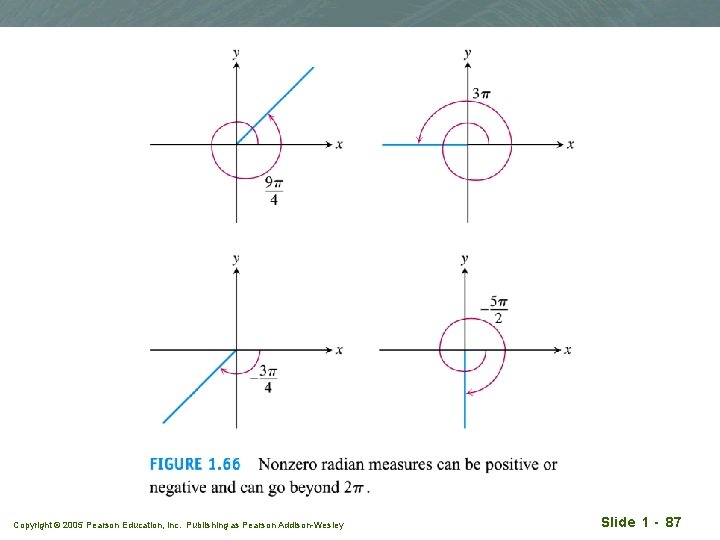
Radian measure Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 84

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 85

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 86

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 87

Angle convention q Be noted that angle will be expressed in terms of radian unless otherwise specified. q Get used to the change of the unit Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 88

The six basic trigonometric functions Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 89

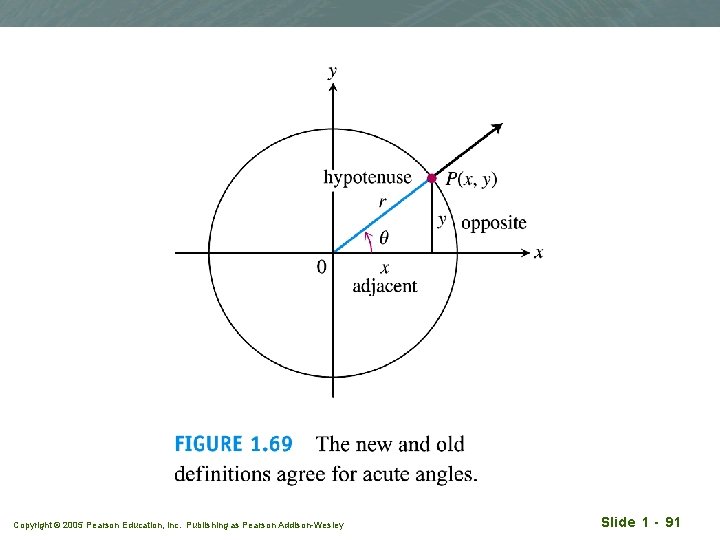
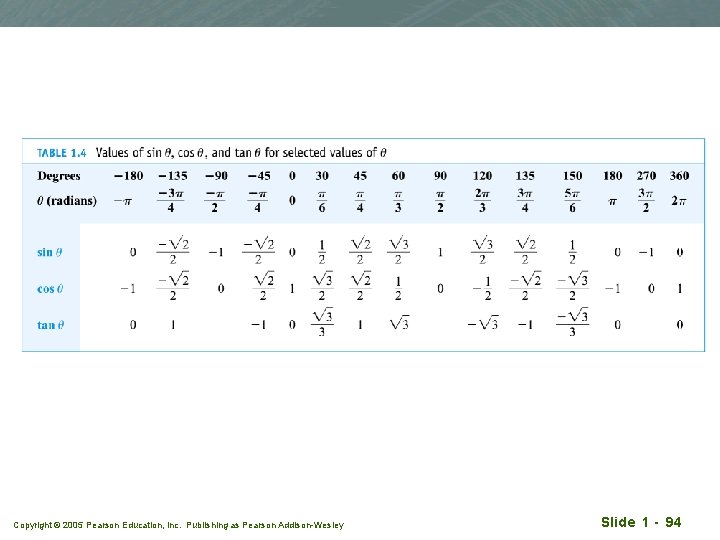
Generalised definition of the six trigo functions q Define the trigo functios in terms of the coordinats of the point P(x, y) on a circle of radius r sinq = y/r q cosine: cosq = x/r q tangent: tanq = y/x q sine: cscq = r/y q secant: secq = r/x q cotangent: cotq = x/y q cosecant: Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 90

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 91

Mnemonic to remember when the basic trigo functions are positive or negative Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 92

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 93

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 94

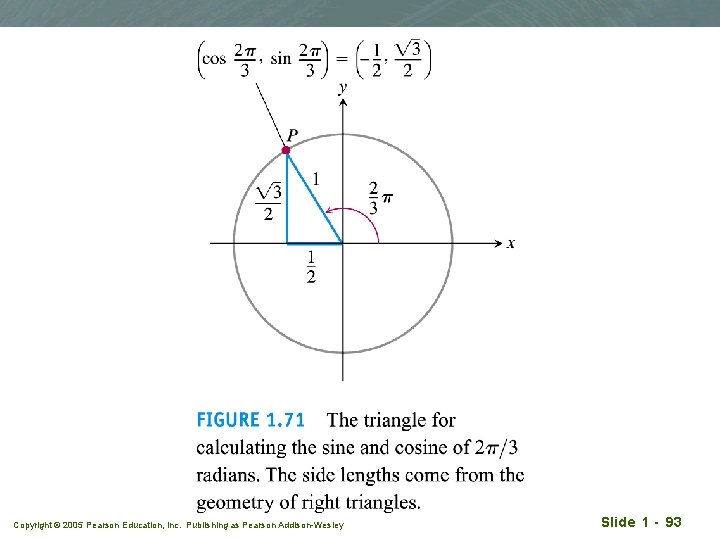
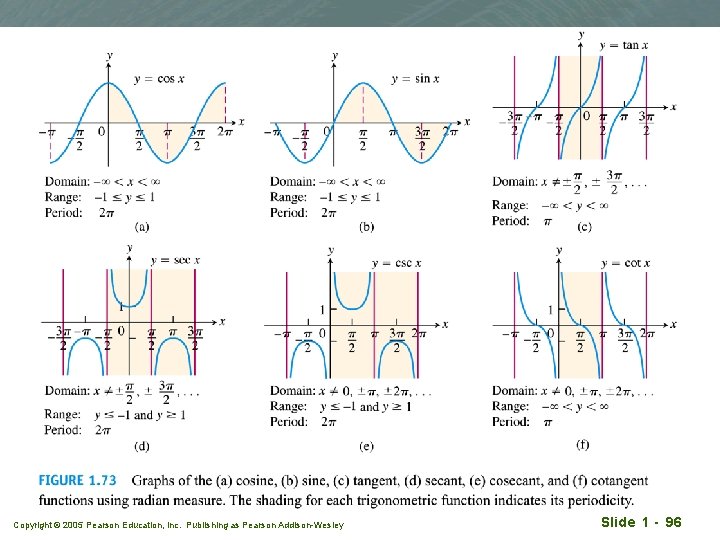
Periodicity and graphs of the trigo functions Trigo functions are also periodic. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 95

Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 96

Parity of the trigo functions The parity is easily deduced from the graphs. Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 97

Identities Applying Pythagorean theorem to the right triangle leads to the identity Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 98

Dividing identity (1) by cos 2 q and sin 2 q in turn gives the next two identities There also similar formulas for cos (A-B) and sin (A-B). Do you know how to deduce them? Slide 1 - 99 Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Identity (3) is derived by setting A = B in (2) Identities (4, 5) are derived by combining (1) and (3(i)) Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 100

Law of cosines c 2= (acosq - b)2 + (asinq)2 = a 2+b 2 -2 abcosq Copyright © 2005 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Slide 1 - 101