Chapter 1 Numbers and Decimal System Ideas of

Chapter 1 Numbers and Decimal System • Ideas of numbers • Representing numbers • The meaning of written numbers • Comparing numbers

1. 1 The Counting (Natural) Numbers • What are numbers? • precise means of representing, and reasoning about quantities. • “how many” and “how much”. • Information about collections of things and quantities of items • How many kinds of numbers do you know? • counting (natural) numbers, negative numbers, decimal numbers, fractions, etc.

Counting (Natural) Numbers • The most basic numbers, and the starting point for young children • What are the counting numbers? 1, 2, 3, 4, …. • Two ways of describing counting numbers: 1. As a list 2. As a cardinality (describing a set size)

Counting Numbers As A List The list of counting numbers: • starts with 1 • every number in the list has a unique successor • every number except 1, has a unique predecessor • every number appears exactly once in this ordered list

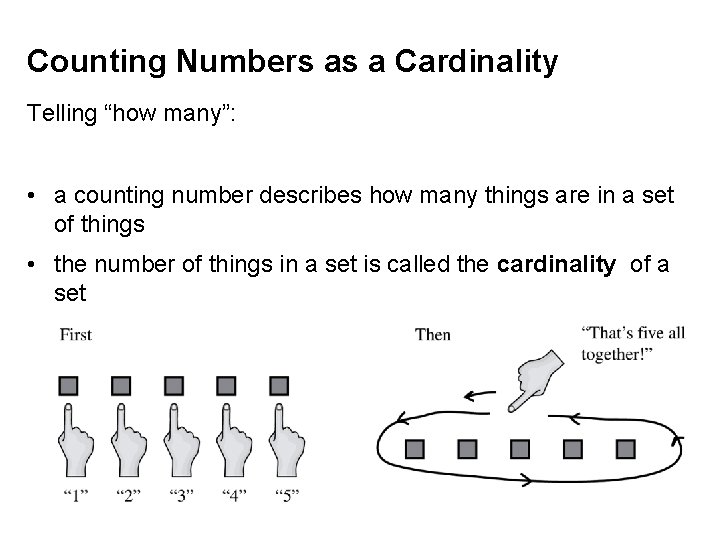
Counting Numbers as a Cardinality Telling “how many”: • a counting number describes how many things are in a set of things • the number of things in a set is called the cardinality of a set

What is a set? A set is a collection of distinct “things” or objects Individual distinct “objects” that form the set are called elements of the set. These elements can be: • concrete, such as chairs in a classroom • abstract, e. g. all counting numbers between 1 and 5 Sets may contain a finite number of elements (e. g. all students in a university) or be ”infinitely long” (e. g. set of all counting numbers)

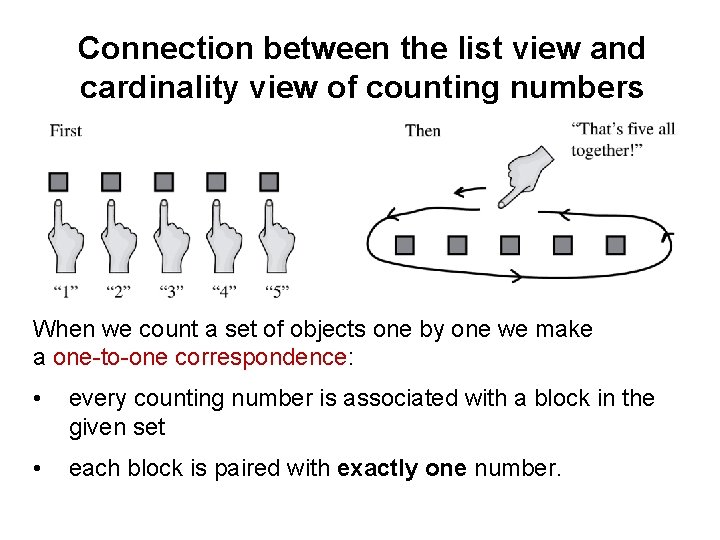
Connection between the list view and cardinality view of counting numbers When we count a set of objects one by one we make a one-to-one correspondence: • every counting number is associated with a block in the given set • each block is paired with exactly one number.

Cardinality refers to how many distinct elements there altogether • The last number we say when we count a set of objects tells us the total number of objects in a set • It is for this reason that the order of counting numbers is so important • Stating at any counting number, the next number in the list, describes the size of the set that has one more element in it

How could a shepherd living thousands of years ago keep track of the sheep?

Representing Counting Numbers and the Origins of the Decimal System • The representation of counting numbers with the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 is a relatively modern invention • These numerals are called Hindu-Arabic numerals • There are other kinds of numeral systems

Brief history of decimal numerals • The Brahmi numerals (India, 3 rd century BC) • Place value system without zero - dot used instead (1 st century BC) • Introduction of the concept of zero (628 CE, by Brahmagupta in “Brahma Sphuta Siddhanta”) • Use of symbol for zero (approximately 9 th century) • Adoption of the numerals in Syria (7 th century) • First appearance in Europe in 976 • Promoted by Fibonacci in 1202 • Wide use in 15 th century and modern form in 16 th century

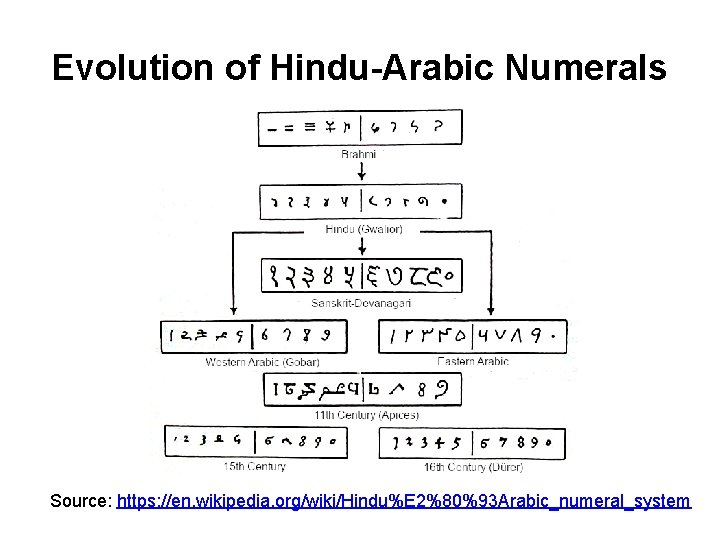
Evolution of Hindu-Arabic Numerals Source: https: //en. wikipedia. org/wiki/Hindu%E 2%80%93 Arabic_numeral_system

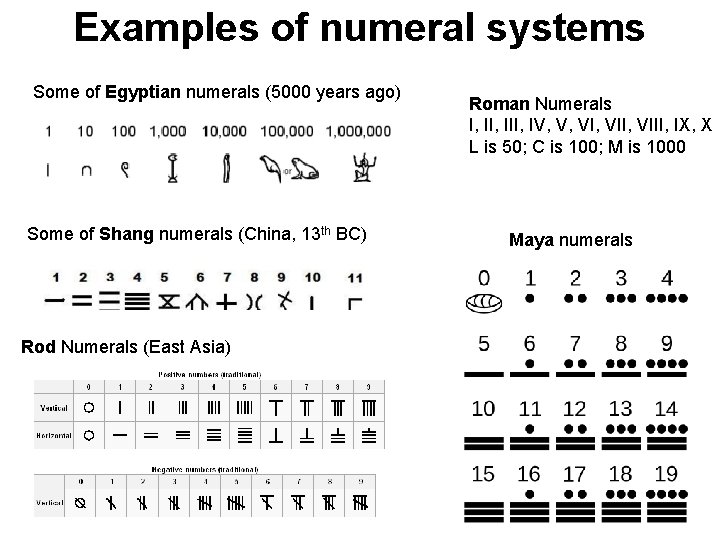
Examples of numeral systems Some of Egyptian numerals (5000 years ago) Some of Shang numerals (China, 13 th BC) Rod Numerals (East Asia) Roman Numerals I, III, IV, V, VII, VIII, IX, X L is 50; C is 100; M is 1000 Maya numerals

Decimal system • There are infinitely many counting numbers • How can each counting number be represented in its own unique way? • The Decimal System (base ten system) • The decimal system requires using only ten distinct symbols, namely the digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 • The key feature of the decimal system is rather than using new symbols to represent larger and larger numbers, it uses place value • This is also true for other positional number systems (e. g. binary, octal, duodecimal, hexadecimal, vigesimal)

Place Value For The Base Ten System Place value (or positional) system: the quantity that a digit in a number represents depends – in a very specific way – on the position of the digit in the number

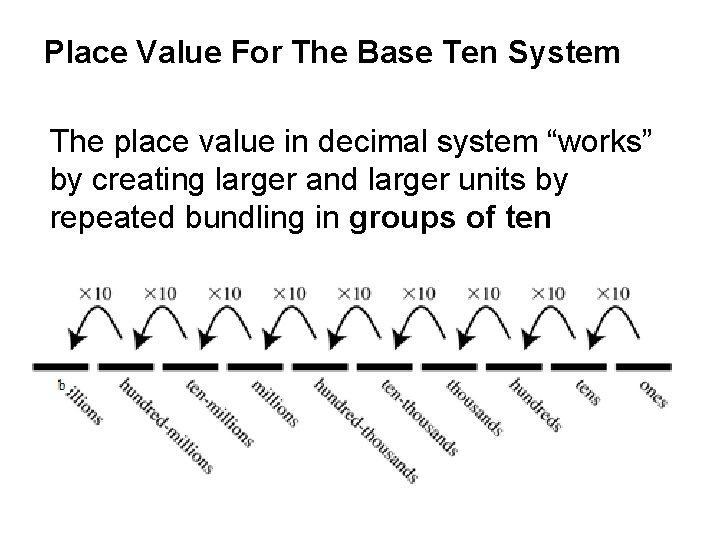
Place Value For The Base Ten System The place value in decimal system “works” by creating larger and larger units by repeated bundling in groups of ten

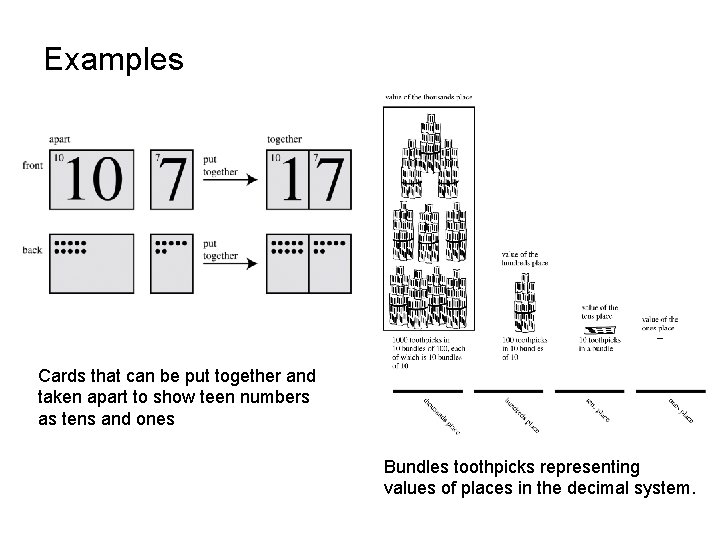
Examples Cards that can be put together and taken apart to show teen numbers as tens and ones Bundles toothpicks representing values of places in the decimal system.

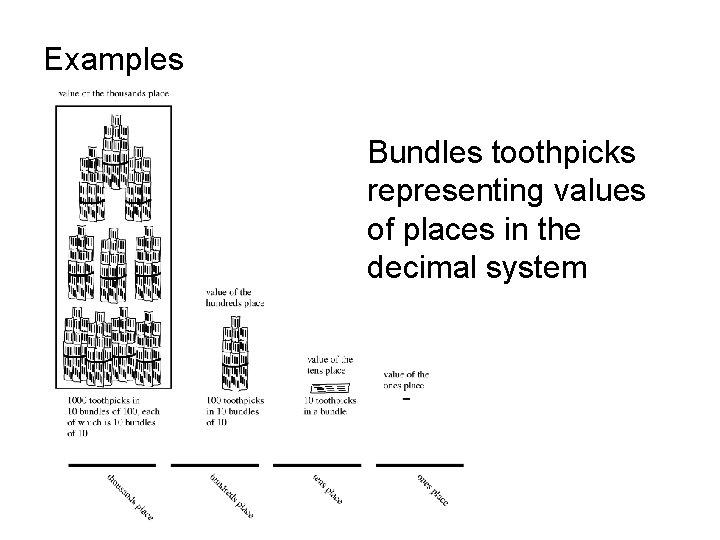
Examples Bundles toothpicks representing values of places in the decimal system

Note Children extend their understanding of the decimal system in two ways • when they view a group of ten as a unit in its own right: 1 group of ten = 10 • when they realize that a two digit number such as 37 stands for 3 tens and 7 ones

What is a decimal representation and what is an expanded form? • A string of digits that represent a number, such as 1234, is called the decimal representation • To clarify the meaning of the decimal representation of a number, we can write it in the expanded form: 1234 = 1 thousand + 2 hundred + 3 tens + 4 ones 1234 = 1 x 1000 + 2 x 100 + 3 x 10 + 4 1234 = 1000 + 200 + 30 + 4 • All three ways are correct and represent the expanded form

0 - Zero • Zero represent the number of elements in a special set, that is called empty set, and contains no elements • The notion of zero may seem natural, but the symbol for the concept of “nothing” or “having none” was introduced far later than counting numbers • It is believed that he concept of zero, as well as notation for it, was first introduced in Egypt around 1800 BC • Olmec culture (territory of modern-day Mexico) used zero before 4 th century BC (long before zero came to use in Europe – Greeks started to use it around 130 AD)

The Whole Numbers • The whole numbers are the counting numbers together with zero, as follows: 0, 1, 2, 3, 4, 5, 6, … • The discovery of zero helped to write arbitrary big numbers in base ten system

The Counting Numbers on Number Paths If a path is labeled with successive counting numbers, we call the path a number path:

The Whole Numbers on the Number Line • To form a number line, mark a location on an infinite line as zero 0, and at same length intervals to the right of 0 mark locations for 1, 2, 3, and so on. • The distance between two neighbor locations (e. g. 0 and 1, 1 and 2, etc) is called a unit • The choice of a unit is called a scale

Other positional systems • Base 60 system (Babylon, 5000 years ago) • Base 20 system (Maya, Inuit) • Base 12 system (some places in Africa, Nepal, India, Ireland, England) • Base 8 system (First Nations in California and Mexico, possibly proto-Indo-Europeans, computers) • Base 2 system (Computers, electronics)

Base 60 – Babylonian numerals Sumer, about 5000 years ago; Babilonia

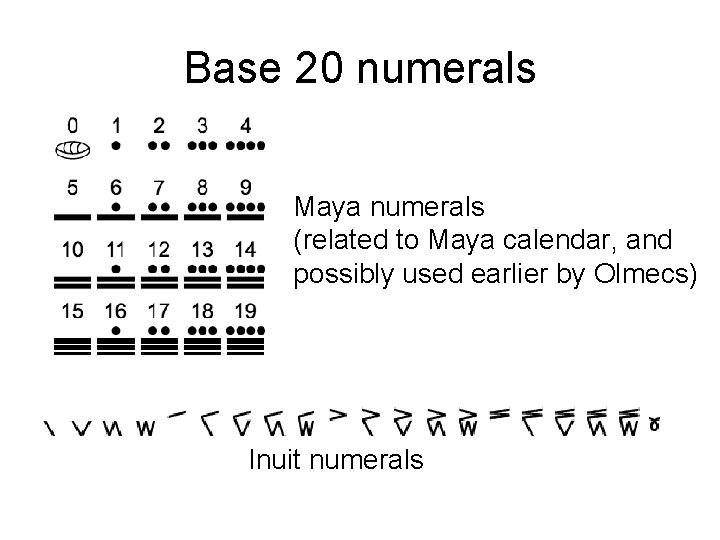
Base 20 numerals Maya numerals (related to Maya calendar, and possibly used earlier by Olmecs) Inuit numerals

Base 2 - Binary system • Uses multiples of 2 instead of multiples of 10: 2, 4, 8, 16, etc. • Digits: 0 and 1 • Examples:

Base 2 - Binary system • Uses multiples of 2 instead of multiples of 10: 2, 4, 8, 16, etc. • Digits: 0 and 1 • Examples: Decimal Binary 0 0 1 1 2 10 3 11 4 100

Negative Numbers • Whole numbers (naturals and zero) are sufficient for addition, but not for subtraction • Other uses of negative numbers: loss, debt, temperature, etc. • The concept of negative numbers first appeared in ”Nine Chapters on the Mathematical Art” (China 202 BC – AD 220) • Europe: only in 16 th century

Negative Numbers … … The whole numbers and the negative numbers together form another infinite set of numbers called the integers

• Write the number represented by the following. What assumption did you make ? • If the little cubes are ones then the number is 325. • If the strips are considered as the ones, then the number is 32. 5 • If the flats are considered as the ones, then the number is 3. 25

Rational Numbers • Now, we have numbers for addition, multiplication, subtraction, but not for division • We must consider ratios of integers such as ½ =0. 5; 2/3 = 0. 66666…, etc

Rational Numbers A rational number is defined as a number that can be written as a fraction of two integer numbers a / b, where b is not zero.

Decimals Extend the Decimal System • Dividing 1 unit into 10 equal places creates a new place value - the tenth, which is recorded to the right of the ones place value after the decimal point • At the tenths place, dividing a tenth into 10 equal pieces creates a hundredth, and the hundredths are recorded in the place to the right of the tenths after the decimal point, and so on

Decimal Notation • In decimal system, a number is represented as a string of digits, possibly including a decimal point, and possibly having infinitely many nonzero digits to the right of the decimal point • This is called decimal notation and the number itself is called decimal (or a decimal number). • Decimal Representation: 2. 345 • Decimal Expansion:

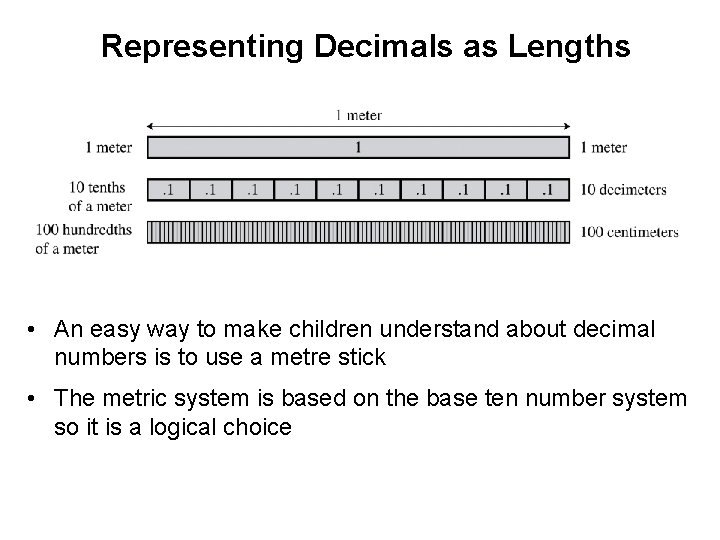
Representing Decimals as Lengths • An easy way to make children understand about decimal numbers is to use a metre stick • The metric system is based on the base ten number system so it is a logical choice

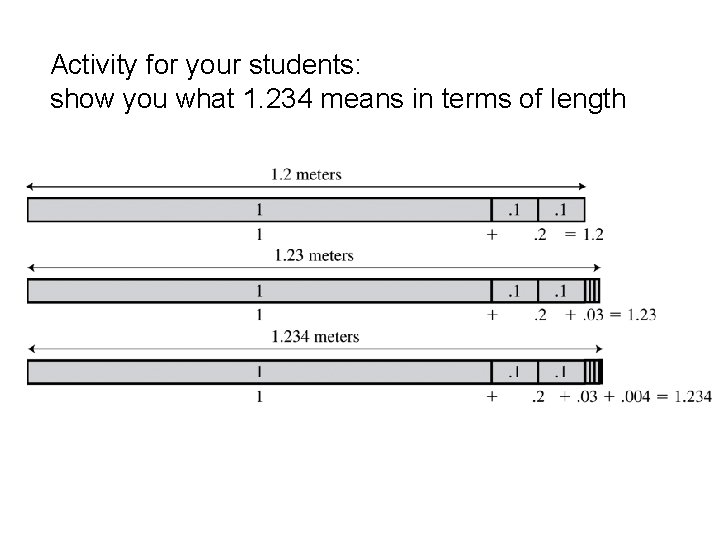
Activity for your students: show you what 1. 234 means in terms of length

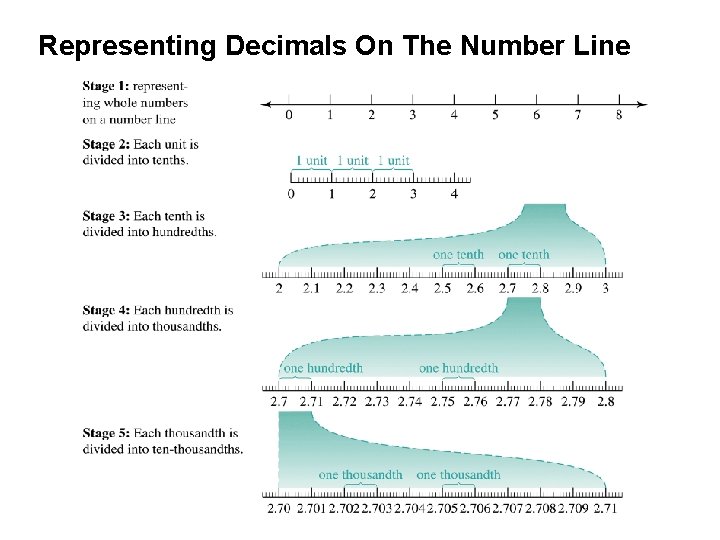
Representing Decimals On The Number Line

Reading the Decimals In reading the decimals, the cultural convention is to say them according to the value of the rightmost nonzero decimal place and to say “and” or ”point” for the decimal point. Examples: 3. 84 three and eighty four hundredths; or three point eight four 1. 592 one and five hundred and ninety two thousandths; or 1 point five nine two

Decimals with Infinitely Many Nonzero Entries and Repeating Pattern • There are decimal numbers that extend infinitely far to the right and form a repeating pattern • Examples: 1/3 = 0. 333… 23/11 = 2. 090909…. 1/28 = 0. 03571428. . . • It can be shown that such numbers are necessarily rational numbers • Any rational number has either finitely many non-zero decimal entries or infinitely many entries that form a repeating pattern

Decimals with Infinitely Many Nonzero Entries and Non-Repeating Pattern • There also decimal numbers that extend infinitely far to the right and do not repeat in a pattern • Examples: π = 3. 141592653…. • Such numbers are called irrational

Example: Fibonacci numbers and the Golden ratio • Start with 1 and 1 • The next number is 1+1 =2, so we have 1, 1, 2 • The next number is 1+2 =3, so now we have 1, 1, 2, 3 • The next number is 2+3 = 5, so now 1, 1, 2, 3, 5 • And so on: each time the next number is obtained as the sum of two previous numbers • 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ….

Example: Fibonacci numbers and the Golden ratio • Leonardo of Pisa, also known as Fibonacci • In his book “Liber Abaci” (1202) he posed and solved a problem involving the growth of a population of rabbits based on idealized assumptions • However, the Fibonacci numbers have been known in India since approximately 200 BC • Fibonacci also popularized decimal system in the West and encouraged its use for bookkeeping

Example: Fibonacci numbers and the Golden ratio • Exercise: compute the ratios of two subsequent Fibonacci numbers

Example: Fibonacci numbers and the Golden ratio 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … 1/1 = 1 2/1 = 2 3/2 = 1. 5 8/5 = 1. 6 13/8 = 1. 625 21/13 = 1. 615 34/21 = 1. 619. . . 55/34 = 1. 617. . .

Example: Fibonacci numbers and the Golden ratio 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … 1/1 = 1 2/1 = 2 3/2 = 1. 5 8/5 = 1. 6 13/8 = 1. 625 21/13 = 1. 615 34/21 = 1. 619. . . 55/34 = 1. 617. . . The Golden ratio

Comparing Numbers in The Decimal System If A and B are two nonnegative quantities (numbers) and A is a larger quantity than B; we write: It is the same as to say that B is a smaller than A:

How one compares numbers in the decimal system? Given two positive numbers, and starting from the place of largest value represented (the left-most place), compare the digits of both given numbers: • If the digits in the place are not equal, then the decimal number with the larger digit is greater than the other number • If the digits in that place are equal, keep moving one place to the right, comparing the digits of the numbers in like places, until one of the numbers is larger than the other number.

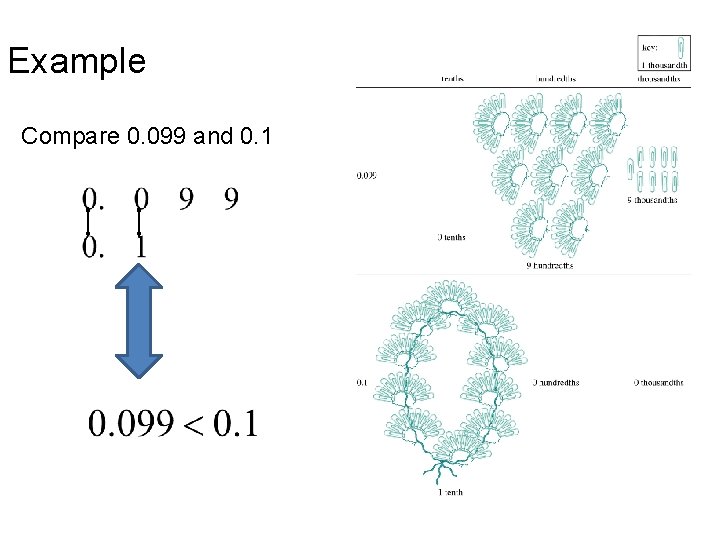
Example Compare 0. 099 and 0. 1

Exception to the rule for comparing numbers in the decimal system The exception occurs when one of the numbers has an infinitely repeating 9, such as: 37. 569999…… In such a case 37. 57 = 37. 569999….

Why does it happen? • Why is 0. 9999…. the same as 1? • Because there are no numbers between 0. 9999… and 1

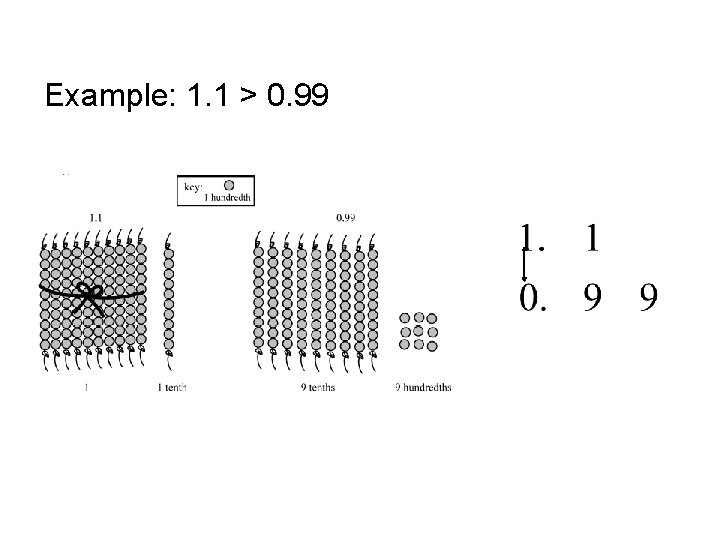
Example: 1. 1 > 0. 99

Using Number Lines To Compare Numbers Small Large

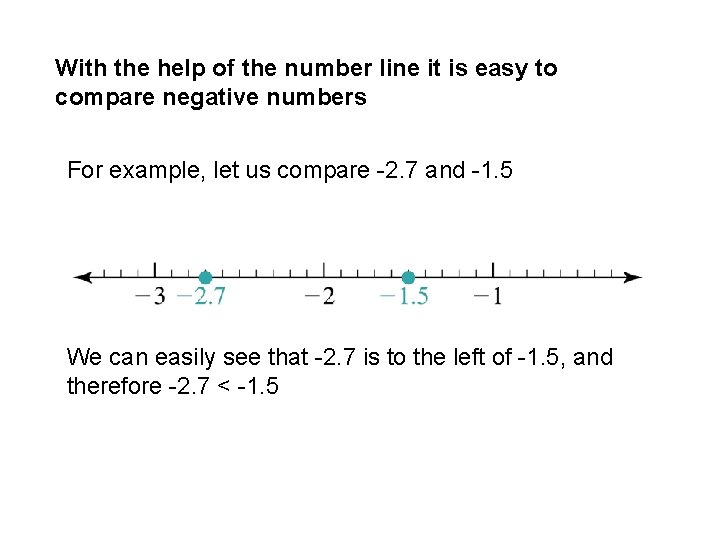
With the help of the number line it is easy to compare negative numbers For example, let us compare -2. 7 and -1. 5 We can easily see that -2. 7 is to the left of -1. 5, and therefore -2. 7 < -1. 5

Comparing Negative Numbers by Viewing Them as Owed Amounts • Think of -2. 7 as owing $2. 70 and of -1. 5 as owing $1. 50 • If you owe $ 2. 70 you have less than if you owe $ 1. 50 • In general, the more you owe, the less you have • That can be represented as: if A > B then - A < - B so since 7 > 4 we have - 7 < - 4 if A < B then - A > - B so since 1. 5 < 2. 7 we have - 1. 5 > 2. 7

Summary • The value of a decimal place is greater than the largest number that can be made using places of lower value (i. e. 1000 > 999) • For this reason, we compare numbers in the decimal system by looking first at the place of the greatest value, then moving to places of lower value, if the numbers are identical in the place with the greater value. • On the number line, numbers become greater as one moves to the right • Taking the negative of two numbers, reverses the comparison between them

Rounding Numbers • To round a number means to find a nearby number that has fewer (or not more) nonzero digits • We can round to the nearest 100, nearest 1, nearest tenth, nearest hundredth, and so on…

Rounding Numbers Example: round 3367 to the nearest hundred • On the number line we see that 3367 is between 3300 and 3400 • 3367 is closer to 3400 than 3300 • Thus 3367 ≈ 3400.

What do we do about numbers that are half way between two tick marks? There are two conventions: The round up convention: when rounding 3450 to the nearest hundred you round up to 3500. When rounding 27. 85 to the nearest tenth, you round up to 27. 9 The engineer convention (significant figures): round to the nearest even number when there is a tie. When rounding 27. 85 to the nearest tenth we round to 27. 8 since 8 is even.

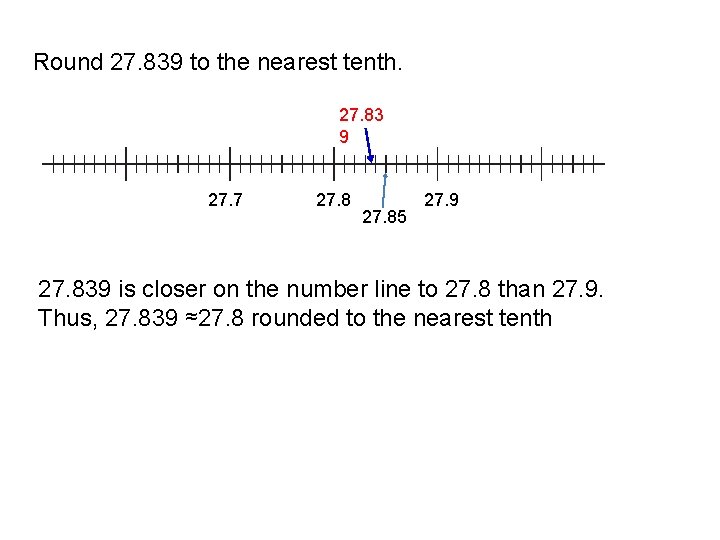
Round 27. 839 to the nearest tenth. 27. 83 9 27. 7 27. 85 27. 9 27. 839 is closer on the number line to 27. 8 than 27. 9. Thus, 27. 839 ≈27. 8 rounded to the nearest tenth

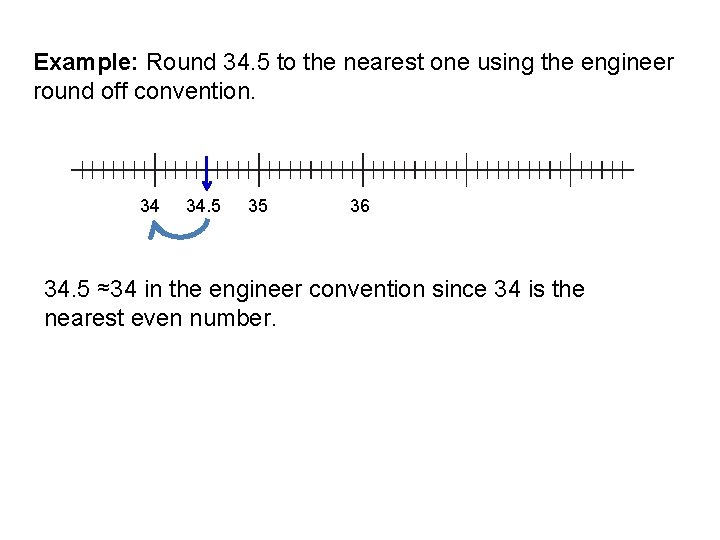
Example: Round 34. 5 to the nearest one using the engineer round off convention. 34 34. 5 35 36 34. 5 ≈34 in the engineer convention since 34 is the nearest even number.

Real world application No matter how precise the modern measuring tools are, they do not have absolute precision Therefore when we work with actual quantities, the way the number is written generally, indicates the rounding that takes place, and therefore the precision with which the quantity is known

Real world application • Another example is the use of calculators or computers for calculations which will give you only approximate value for many computations • For example, 1/3 = 0. 3333333…. (infinite sequence of digits), while calculator would give you something like 0. 3333, which is a rounded value • The same happens when you use calculators to deal with irrational numbers or with numbers whose after the decimal point length exceed the precision of a calculator

Where in the class can you use the rounding concept? • Measurement • Estimating • Quick check of the answers