Chapter 1 Number Systems Number Representations and Codes

Chapter 1 Number Systems, Number Representations, and Codes Digital Design Lab

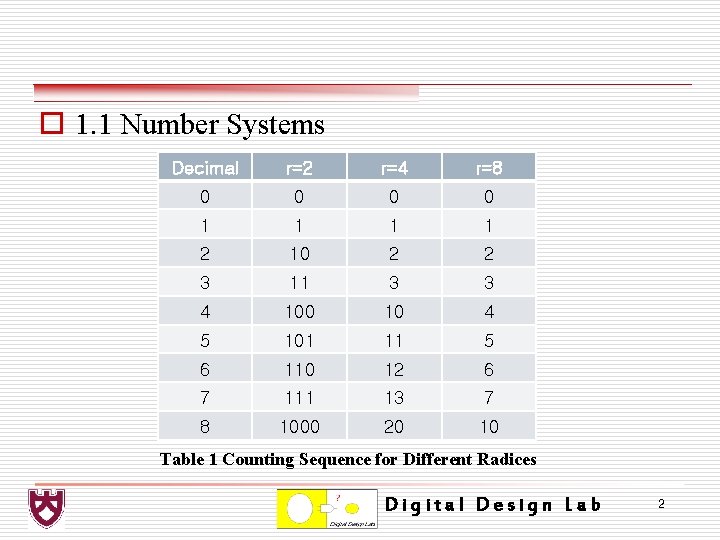
o 1. 1 Number Systems Decimal r=2 r=4 r=8 0 0 1 1 2 10 2 2 3 11 3 3 4 100 10 4 5 101 11 5 6 110 12 6 7 111 13 7 8 1000 20 10 Table 1 Counting Sequence for Different Radices Digital Design Lab 2

o 1. 1. 1 Binary Number System Ø The radix is 2 in the binary number system; therefore, only two digits are used: 0 and 1. Ø The weight assigned to each position of a binary number is as follows: 2 n-1 2 n-2. . . 23222120. 2 -12 -22 -3. . . 2 -m 1 0 1 1. 1 0 12 = (1 × 23)+(0 × 22) +(1 × 21) +(1 × 20) + (1 × 2 -1) +(0 × 2 -2) +(1 × 2 -3) = 11. 62510 Digital Design Lab 3

Ø A binary number is a group of n bits that can assume 2 n different combinations of the n bits. The range for n bits is 0 to 2 n -1. Ø Table 2 shows the weight associated with each of the four binary positions. Decimal Binary 8 4 2 1 23 22 21 20 0 0 0 8 1 0 0 0 1 9 1 0 0 1 2 0 0 10 1 0 3 0 0 1 1 11 1 0 1 1 4 0 1 0 0 12 1 1 0 0 5 0 1 13 1 1 0 1 6 0 1 1 0 14 1 1 1 0 7 0 1 15 1 1 Table 2 Counting in Binary Digital Design Lab 4

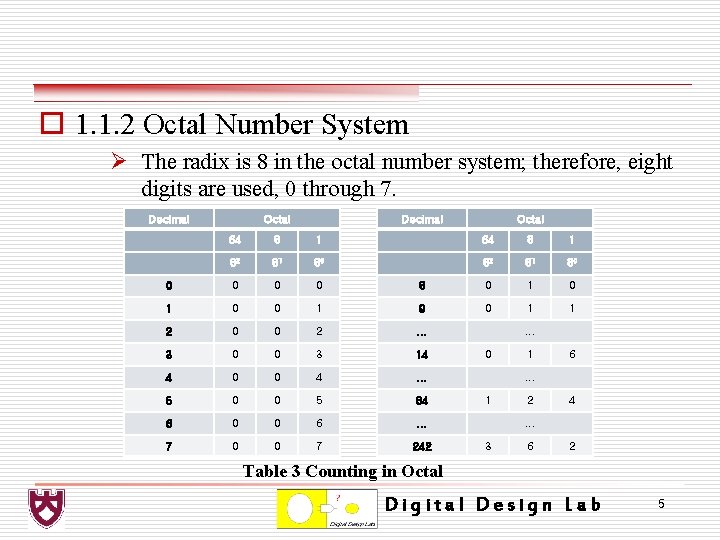
o 1. 1. 2 Octal Number System Ø The radix is 8 in the octal number system; therefore, eight digits are used, 0 through 7. Decimal Octal 64 8 1 82 81 80 0 0 8 0 1 0 0 1 9 0 1 1 2 0 0 2 . . . 3 0 0 3 14 4 0 0 4 . . . 5 0 0 5 84 6 0 0 6 . . . 7 0 0 7 242 . . . 0 1 6 . . . 1 2 4 . . . 3 6 2 Table 3 Counting in Octal Digital Design Lab 5

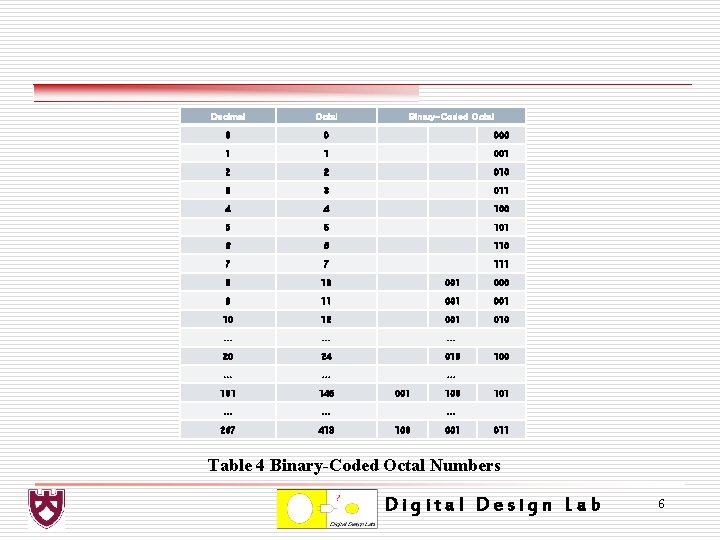
Decimal Octal Binary-Coded Octal 0 0 000 1 1 001 2 2 010 3 3 011 4 4 100 5 5 101 6 6 110 7 7 111 8 10 001 000 9 11 001 10 12 001 010 . . 20 24 010 . . 101 145 . . . 267 413 001 100 101 . . . 100 001 011 Table 4 Binary-Coded Octal Numbers Digital Design Lab 6

o 1. 1. 3 Decimal Number System Ø The radix is 10 in the decimal number system; therefore, ten digits are used, 0 through 9. Decimal Binary-Coded Octal 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 10 0001 . . . 124 0001 . . . 365 0010 0000 0100 . . . 0011 0110 Binary-coded decimal • Each decimal digit can be encoded into a corresponding binary number; however, only ten decimal digits are valid. • Therefore, four binary digits are required to represent each decimal digit. 0101 Table 5 Binary-Coded Decimal Numbers Digital Design Lab 7

o 1. 1. 4 Hexadecimal Number System Ø The radix is 16 in the hexadecimal number system. Decimal Hexadecimal Binary-Coded Octal 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 10 A 1010 11 B 1011 12 C 1100 13 D 1101 14 E 1110 15 F 1111 Binary-coded hexadecimal • All 24 values of the four binary bits are used to represent the 16 hexadecimal digits. • Each hexadecimal digit corresponds to a 4 -bit binary number as shown in Table 6 BCH Numbers Digital Design Lab 8

o 1. 1. 5 Arithmetic Operations Radix 2 Addition and carry 1 to the next column Example: carries Digital Design Lab 9

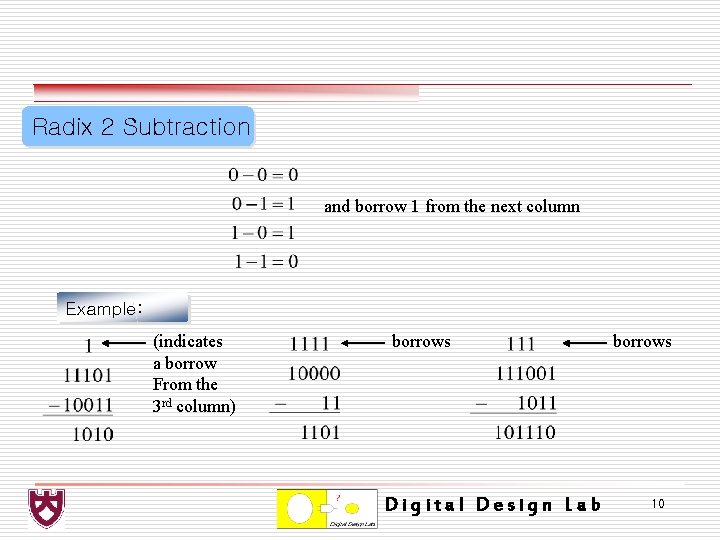
Radix 2 Subtraction and borrow 1 from the next column Example: (indicates a borrow From the 3 rd column) borrows Digital Design Lab borrows 10

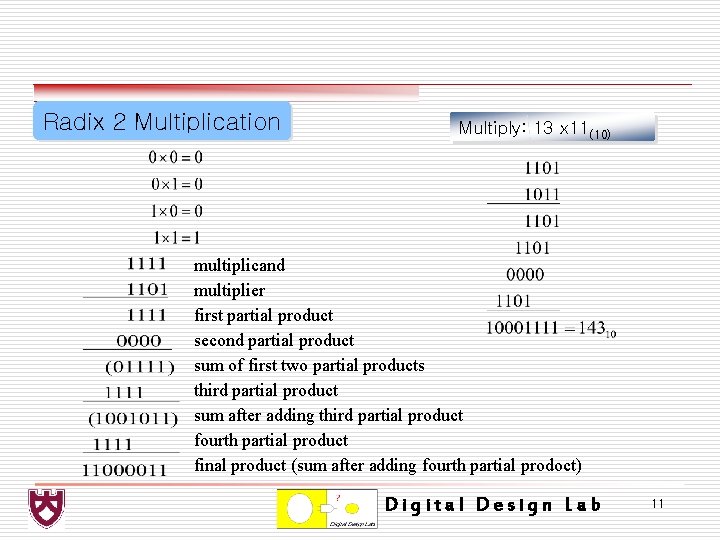
Radix 2 Multiplication Multiply: 13 x 11(10) multiplicand multiplier first partial product second partial product sum of first two partial products third partial product sum after adding third partial product fourth partial product final product (sum after adding fourth partial prodoct) Digital Design Lab 11

Radix 2 Division The quotient is 1101 with a remainder of 10. Digital Design Lab 12

o 1. 1. 6 Conversion Between Radices ü Convert from radix ri to any other radix rj Ø 1259 =(1× 92) +(2× 91)+(5× 90)=10410 Ø Convert 10410 to radix 7. 104 ÷ 7 = quotient = 14, remainder=6 (6 is the low-order digit) 14 ÷ 7 = quotient = 2, remainder=0 2 ÷ 7 = quotient = 0, remainder=2 Verify the answer 1259 = 2067 = (2× 72) + (0× 71) + (6× 70) = 10410 Digital Design Lab 13

Ø Octal to hexadecimal v To convert from octal to hexadecimal, the octal number is first converted to BCO then partitioned into 4 -bit segments to form binary-coded hexadecimal(BCH). v The BCH notation is then easily changed to hexadecimal, as shown below. 7 6 3 5 . 4 6 1 1 1 0 0 1 1 1 0 1. 1 0 0 11 0 0 0 F 9 D . 9 8 Digital Design Lab 14

o 1. 2 Number Representations Ø The leftmost(high-order) digit is usually reserved for the sign of the number. Ø A = (an-1 an-2 an-3. . . a 2 a 1 a 0)r Ø where digit an-1 has the following value: A= 0 if A≥ 0 r-1 if A<0 Digital Design Lab 15

o 1. 2. 1 Sign Magnitude Ø A = (0 an-2 an-3. . . a 1 a 0)r Ø A'= [(r -1)an-2 an-3. . . a 1 a 0]r ü There are two problems with sign-magnitude representation. Ø First, there are two representations for the number 0; specifically +0 and -0; ideally there should be a unique representation for the number 0. Ø Second, when adding two numbers of opposite signs, the magnitudes of the numbers must be compared to determine the sign of the result. Digital Design Lab 16

o Examples 0 1 0 0 0 0 1 0 0 +4 − 4 Magnitude Sign 0 0 1 1 0 0 0 1 Radix 10 0 7 4 9 7 4 1 0 1 3 3 +13. 625 − 13. 625 +743 − 743 Digital Design Lab 17

o 1. 2. 2 Diminished-Radix Complement A = (0 an-2 an-3. . . a 1 a 0)r A'= [(r− 1)an-2'an-3'. . . a 1'a 0']r (ai' = (r − 1) −ai ) Positive integers: 0 to 2 n− 1− 1 Negative integers: 0 to −(2 n− 1− 1) 27 0 27 1 26 0 26 1 25 0 24 1 24 0 23 1 23 0 22 1 22 0 21 1 20 0 20 1 +6010 − 6010 Digital Design Lab 18

o 1. 2. 3 Radix Complement Ø A = (0 an-2 an-3. . . a 1 a 0)r Ø (A')+1= {[(r− 1)an-2'an-3'. . . a 1'a 0']+1}r Number Representation Positive Numbers Negative Numbers Sign magnitude 0 an-2 an-3. . . a 1 a 0)r (r -1)an-2 an-3. . . a 1 a 0 Diminished-radix complement 0 an-2 an-3. . . a 1 a 0)r (r− 1)an-2'an-3'. . . a 1'a 0' Radix complement 0 an-2 an-3. . . a 1 a 0)r (r− 1)an-2'an-3'. . . a 1'a 0'+1 Table 8 Number Representations for Positive and Negative Integers of the Same Absolute Value for Radix r Digital Design Lab 19

o 1. 2. 4 Arithmetic Operations ü Binary Addition Ø Overflow A = an-1 an-2 an-3. . . a 1 a 0 B = bn-1 bn-2 bn-3. . . b 1 b 0 Overflow = (an-1 • bn-1 • sn-1') + (an-1' • bn-1' • sn-1) Overflow = cn-1⊕cn-2=(cn-1 • cn-2') +(cn-1' • cn-2) Ø “ • ” -----logical AND “+”-----logical OR “⊕”-----exclusive-OR Ø Cn-1 and Cn-2 are the carry bits out of positions n − 1 and n − 2, respectively. Digital Design Lab 20

ü Binary subtraction A = Minuend − ) B = Subtrahend Difference l Difference = A − B = A − r n + rn − B = A − rn + (rn − B) = A − rn + (B' +1) Digital Design Lab 21

ü Binary multiplication A = an-1 an-2 an-3. . . a 1 a 0 B = bn-1 bn-2 bn-3. . . b 1 b 0 Product of A×B =p 2 n-1 p 2 n-2 p 2 n-3. . . p 1 p 0 A = Multiplicand (n bits) ×) B = Multiplier (n bits) P = Product (2 n bits) Digital Design Lab 22

o Example 0 0 0 0 1 0 ×) 0 0 0 1 1 1 (+7) 1 0 1 (+5) 1 1 1 0 0 0 1 1 (+35) Digital Design Lab 23

ü Binary division Ø Dividend = ( Quotient × Divisor ) + Remainder A = a 2 n-1 a 2 n-2. . . anan-1. . . a 1 a 0 B = bn-1 bn-2 bn-3. . . b 1 b 0 Q = qn-1 qn-2. . . q 1 q 0 R = rn-1 rn-2. . . r 1 r 0 qn-1 = a 2 n-1 ⊕ bn-1 (Dividend) (Divisor) Digital Design Lab 24

o 1. 3 Binary Codes ü 1. 3. 1 Binary Weighted and Nonweighted Codes Table 9 Examples of Binary Codes for Decimal Digits Digital Design Lab 25

o 1. 3. 2 Binary-to-BCD Conversion Ø BCD digits in the range 0 -4 do not require an adjustment after being shifted left, because the shifted number will be in the range 0 -8, which can be contained in a 4 -bit BCD digit. Ø If the number to be shifted is in the range 5 -9, then an adjustment will be required after the left shift, because the shifted number will be in the range 10 -18, which requires two BCD digits. Digital Design Lab 26

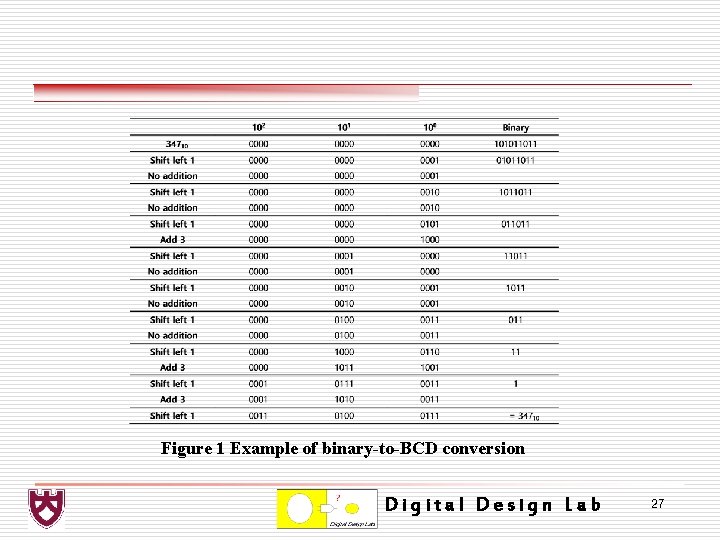
Figure 1 Example of binary-to-BCD conversion Digital Design Lab 27

o 1. 3. 3 BCD-to-Binary Conversion Ø In general, if the high-order bit in any decade is a 1 after the shift-right operation, then a value of 3 must be subtracted from the decade. Digital Design Lab 28

Digital Design Lab 29

o 1. 3. 4 Gray Code ←y 4 is reflected ← y 3 and y 4 are reflected ← y 2, y 3 and y 4 are reflected Table 10 Binary 8421 Code and the Gray Code Digital Design Lab 30

o Binary-to-Gray code conversion Ø Where b 0 and g 0 are the low-order bits of the binary and Gray codes, respectively. Ø The ith Gray code bit gi can be obtained from the corresponding binary code word by the following algorithm: § § gn-1 = bn-1 gi = bi ⊕ bi+1 Digital Design Lab 31

o Gray-to-binary code conversion Ø Where b 0 and g 0 are the low-order bits of the binary and Gray codes, respectively. § § bn-1 = gn-1 bi = bi+1 ⊕ g ü Example g 3 g 2 g 1 g 0 = 1001 b 3 = g 3 =1 b 2 = b 3 ⊕ g 2 = 1 ⊕ 0 = 1 b 1 = b 2 ⊕ g 1 = 1 ⊕ 0 = 1 b 0 = b 1 ⊕ g 0 = 1 ⊕ 1 = 0 Digital Design Lab 32

o 1. 4 Error Detection and Correction Code ü 1. 4. 1 Parity Ø An extra bit can be added to a message to make the overall parity of the code word either odd or even. Ø The number of 1 s in the code word −message bits plus parity bit. v Parity bit(even) = m 3 ⊕ m 2 ⊕ m 1 ⊕ m 0 Digital Design Lab 33

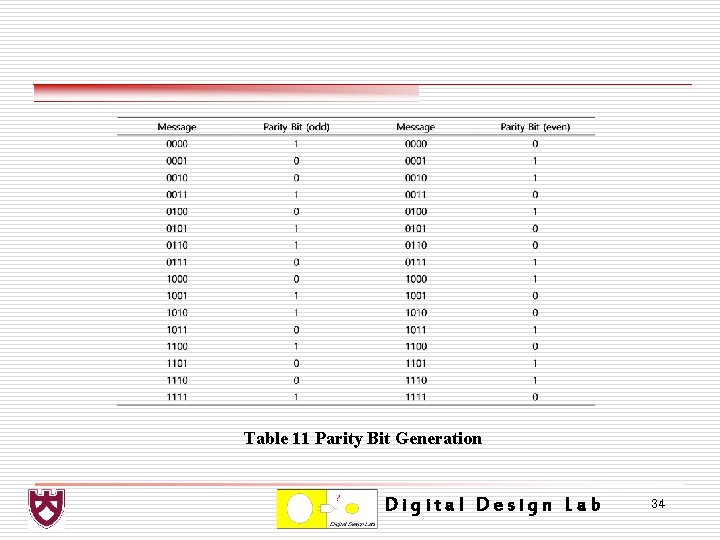
Table 11 Parity Bit Generation Digital Design Lab 34

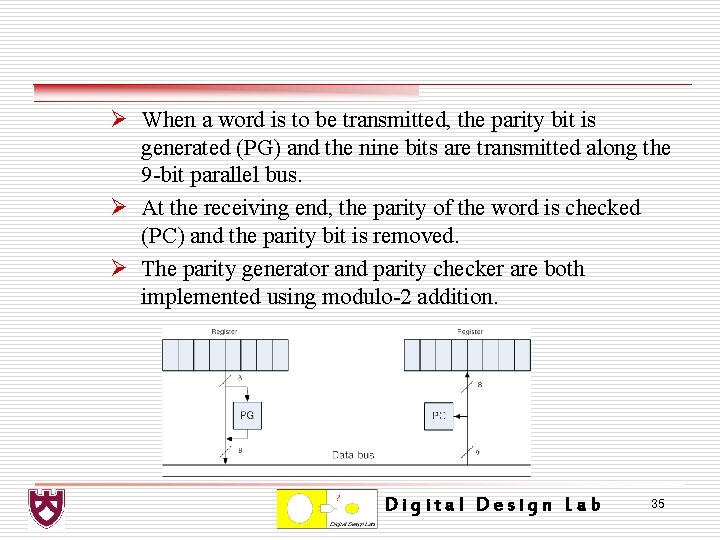
Ø When a word is to be transmitted, the parity bit is generated (PG) and the nine bits are transmitted along the 9 -bit parallel bus. Ø At the receiving end, the parity of the word is checked (PC) and the parity bit is removed. Ø The parity generator and parity checker are both implemented using modulo-2 addition. Digital Design Lab 35

o 1. 4. 2 Hamming Code Ø The Hamming code can be considered as an extension of the parity code presented in the previous section, because multiple parity bits provide parity for subsets of the message bits. Code word X =x 1, x 2, ………, xm+1, … , xn Digital Design Lab 36

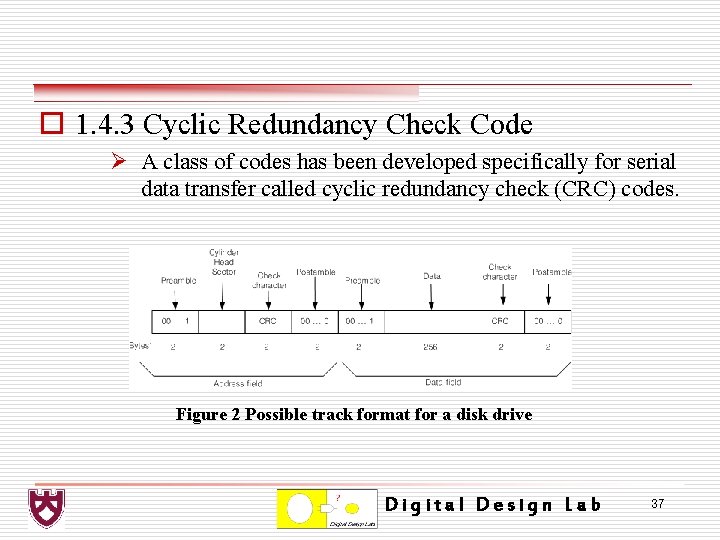
o 1. 4. 3 Cyclic Redundancy Check Code Ø A class of codes has been developed specifically for serial data transfer called cyclic redundancy check (CRC) codes. Figure 2 Possible track format for a disk drive Digital Design Lab 37

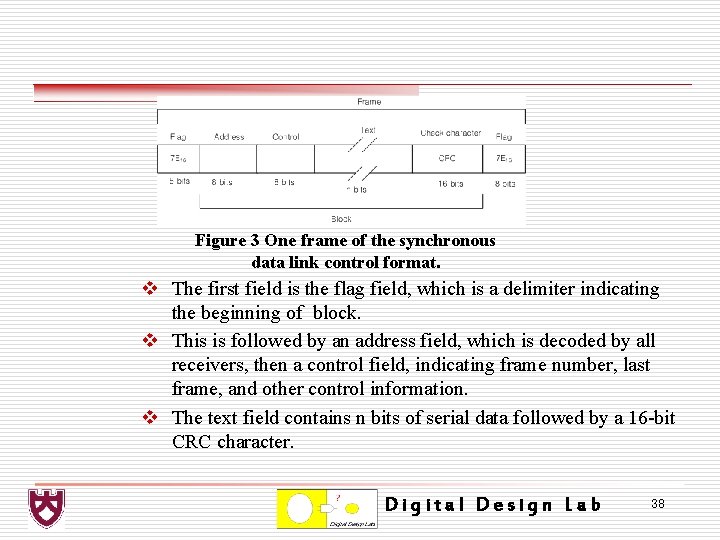
Figure 3 One frame of the synchronous data link control format. v The first field is the flag field, which is a delimiter indicating the beginning of block. v This is followed by an address field, which is decoded by all receivers, then a control field, indicating frame number, last frame, and other control information. v The text field contains n bits of serial data followed by a 16 -bit CRC character. Digital Design Lab 38

o 1. 4. 4 Checksum Ø The checksum is the sum derived from the application of an algorithm that is calculated before and after transmission to ensure that the data is free from errors. Figure 4 Checksum generated for a 4 -byte message. Digital Design Lab 39

o 1. 4. 5 Two-Out-Of-Five Code Ø The two-out-of-five code is 5 -bit nonweighted code that is characterized by having exactly two 1 s and three 0 s in any code word. Table 12 Two-out-of-Five Code for the Decimal Digits Digital Design Lab 40

o 1. 4. 6 Horizontal and Vertical Parity Check Ø An alternative method to Hamming code for smaller memories − which has less redundancy − is a technique using horizontal and vertical parity. Ø Horizontal parity utilizes an odd parity bit for each word in memory. Ø Vertical parity is the modulo-2 addition of identical bit positions of each word in a block of memory. Digital Design Lab 41

Figure 5 Ten-word memory to illustrate singleerror detection and correction using horizontal and vertical parity Digital Design Lab 42

o Example v Assume that word four has an error in bit position four such that word four changes from 0111 1010 0 to 0110 1010 0, which is incorrect for odd parity. v As another example, assume that word seven has an error in bit position two such that word seven changes from 0011 0110 1 to 0011 0010 1, which is incorrect for odd parity. Digital Design Lab 43

o 1. 5 Serial Data Transmission Ø There are two basic types of serial communication: synchronous and asynchronous. v In synchronous communication, information is transferred using a self-clocking scheme; that is, the clock is synchronized to the data, which determines the rate of transfer. v In asynchronous communication, the timing occurs for each character. The communications line for asynchronous serial data transfer is in an idle state (a logic 1 level) when characters are not being transmitted. Digital Design Lab 44

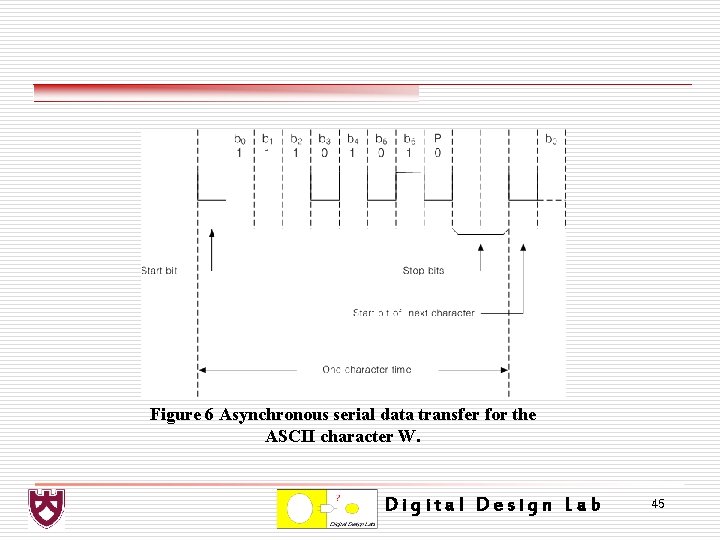
Figure 6 Asynchronous serial data transfer for the ASCII character W. Digital Design Lab 45