Chapter 1 Linear Equations 1 1 Systems of

Chapter 1: Linear Equations 1. 1 Systems of Linear Equations 1. 2 Row Reduction and Echelon Forms

Solve each system of equations

Linear Equation: System of linear equations: A collection of one or more linear equations involving the same variables

• Solution Set The set of all possible solutions to a linear system. • Two linear systems are called equivalent, if they have the same solution set.

Matrix Notation Any linear system can be written as a matrix (rectangular array) whose entries are the coefficients. The size of a matrix tells how many rows and columns it has. (Ex: This is a 2 x 4 matrix. )

For the linear system: The matrix is called the coefficient matrix, and the matrix is called the augmented matrix.

Algorithmic Procedure for Solving a Linear System Basic idea: Replace one system with an equivalent system that is easier to solve. Example: Solve the following system:

/2 /(-2) R 1*(1/2) → R 1 R 2*(-1/2) → R 2 R 1 ↔ R 2 *(-2) +) -2*R 1+R 2 → R 2 /3 R 2*(1/3) → R 2 2*R 2+R 1 → R 1

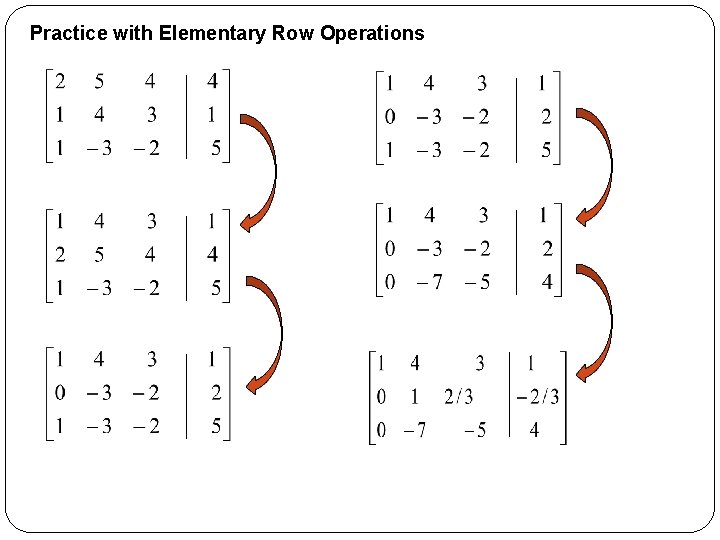
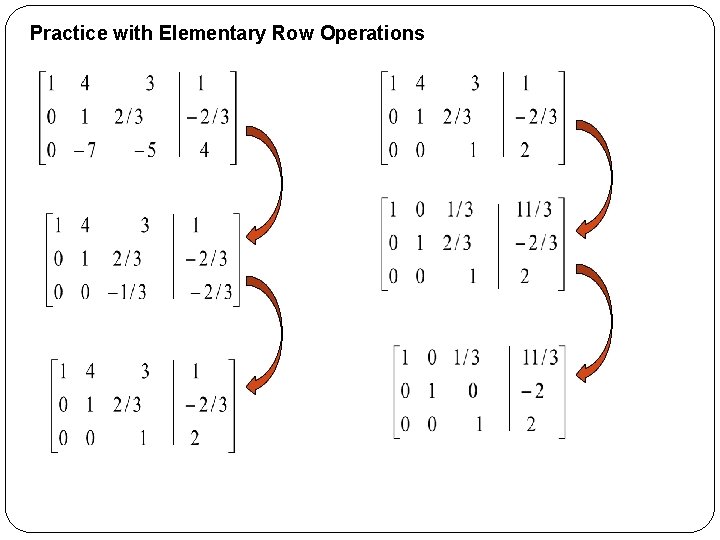
Elementary Row Operations (Theorem 1. 1. 1) Each of the following operations, performed on any linear system, produce a new linear system that is equivalent to the original. 1. Interchange two rows. 2. Add a multiple of one row to another row. 3. Multiply a row by any nonzero constant. R 1 R 2 (-2)R 1+R 2 R 2/(-3) R 2

Gauss-Jordan elimination method to solve a system of linear equations Elementary Row Operations Augmented matrix Reduced row-echelon form

Practice with Elementary Row Operations

Practice with Elementary Row Operations

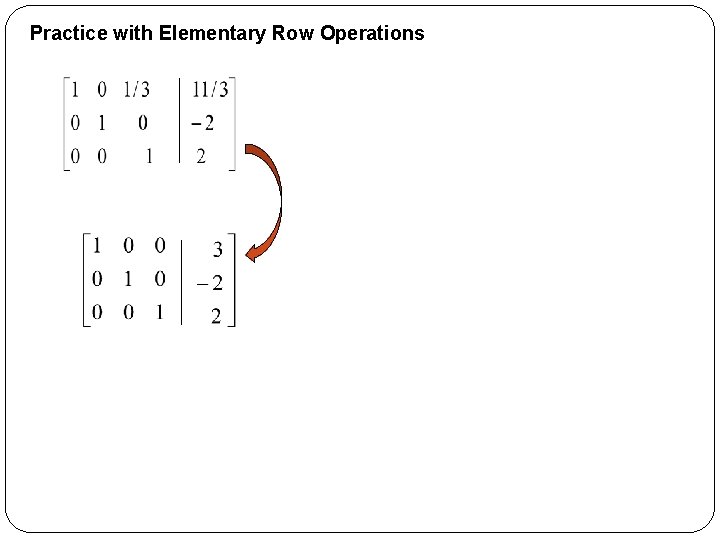
Practice with Elementary Row Operations

Gauss-Jordan elimination method to solve a system of linear equations Elementary Row Operations Augmented matrix Reduced row-echelon form

Definition. A matrix is in reduced row-echelon form if it has the following four properties: 1. The leftmost nonzero entry in each row is 1. (If the row is not all zeros, this entry is called the leading 1. ) 2. Each leading 1 is the only nonzero entry in its column. 3. Each leading 1 of a row is in a column to the right of the leading 1 of the row above it. 4. All nonzero rows are above any rows of all zeros.

Word Problems Example. A certain crazed zoologist is raising experimental animals on a reserve near a toxic waste dump. There are four kinds of animals: Neon dogs have one head, two tails, four eyes and four legs. Headless cats have no head, one tail, no eyes and four legs. Killer ducks have two heads, no tail, four eyes and two legs. Hopping cows have one head, one tail, two eyes and one leg. An investigator finds in the inventory book that there

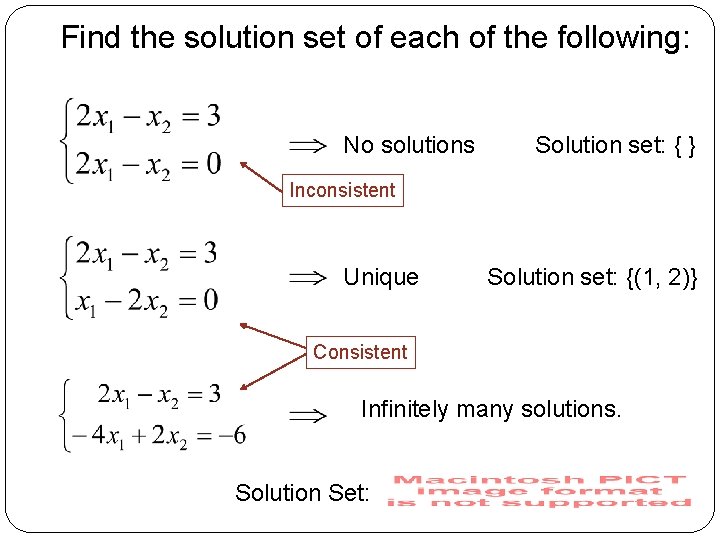
Existence and Uniqueness Is the system consistent; that is, does at least one solution exist? If a solution exists, is it the only one; that is, is the solution unique?

Find the solution set of each of the following: No solutions Solution set: { } Inconsistent Unique Solution set: {(1, 2)} Consistent Infinitely many solutions. Solution Set:

A linear system has one of the following: No solutions, or Exactly one solution, or Infinitely many solutions.

Practice: Writing a solution set