Chapter 1 Introduction Xray Diffraction Crystal Structure Analysis

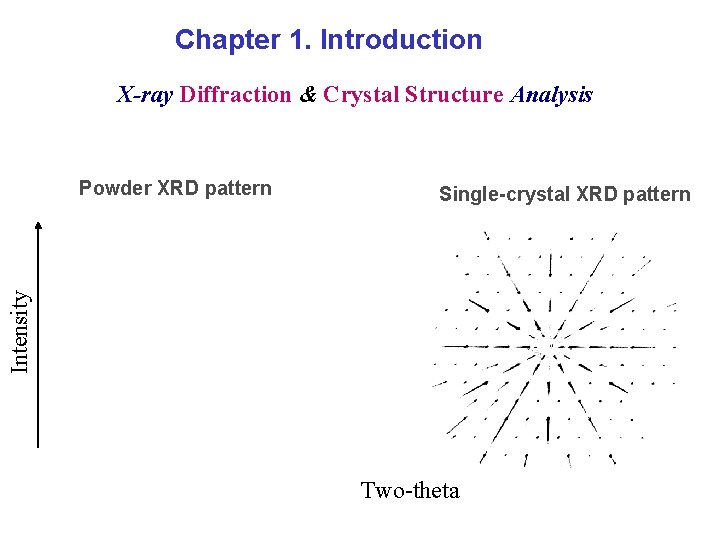
Chapter 1. Introduction X-ray Diffraction & Crystal Structure Analysis Single-crystal XRD pattern Intensity Powder XRD pattern Two-theta

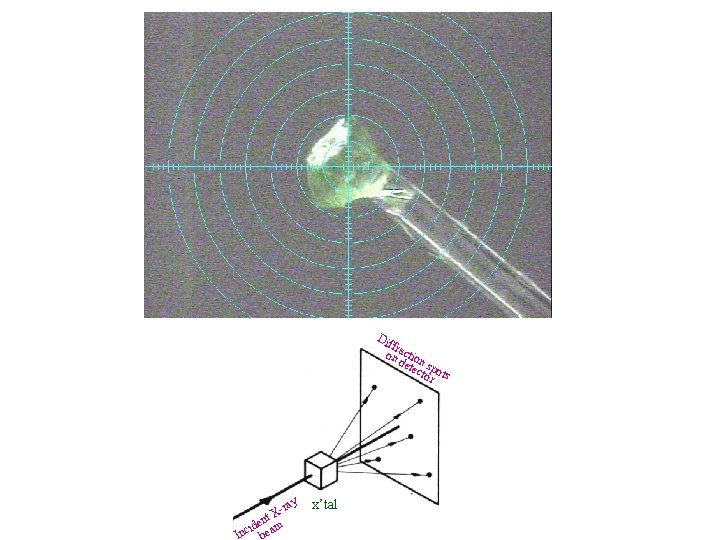
Dif fr on actio det n s ect pot or s ray t. X n e id m Inc bea x’tal

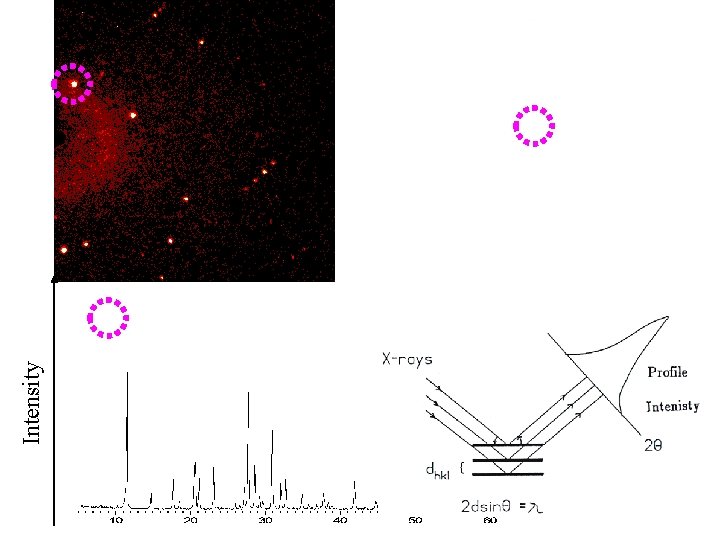
Intensity

Type λ 對空氣穿透率 (10 dm path length) Hard X-rays Soft X-rays <5Å > 80% < 80% Applications: (i) Diffraction for powder, single crystals and partially crystalline materials (ii) Spectroscopy (iii) Spectrometry (medical and industrial)

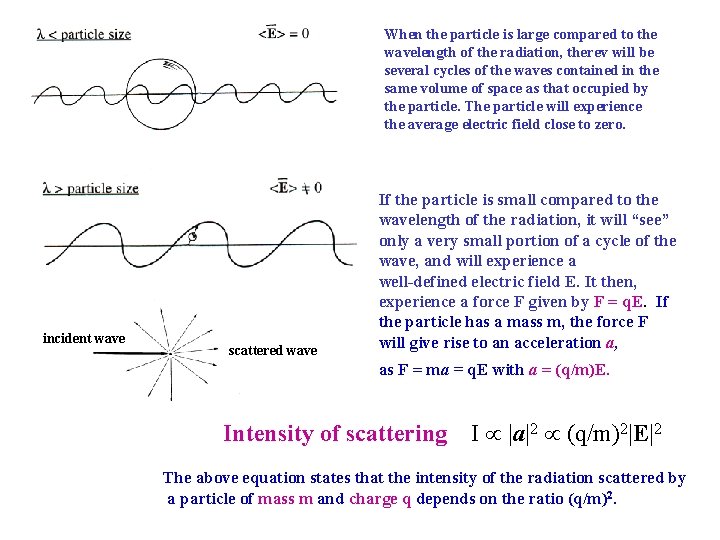
When the particle is large compared to the wavelength of the radiation, therev will be several cycles of the waves contained in the same volume of space as that occupied by the particle. The particle will experience the average electric field close to zero. incident wave scattered wave If the particle is small compared to the wavelength of the radiation, it will “see” only a very small portion of a cycle of the wave, and will experience a well-defined electric field E. It then, experience a force F given by F = q. E. If the particle has a mass m, the force F will give rise to an acceleration a, as F = ma = q. E with a = (q/m)E. Intensity of scattering I |a|2 (q/m)2|E|2 The above equation states that the intensity of the radiation scattered by a particle of mass m and charge q depends on the ratio (q/m)2.

X-rays are scattered by electrons Neutrons have no charge and will not scatter X rays. Protons have the elemental charge e, and a mass mp, and electrons also have the elemental charge e, but a mass me. A proton, however, is 1837 times heavier than an electron, i. e. mp = 1837 me. The intensities of radiation scattered by an electron Ie and that by a proton Ip are Ie / Ip = (e/me)2(mp/e)2 = 18372 X-ray diffraction therefore looks at the electron distribution in a crystal, and not directly at the positions of the nuclei of atoms.

Chapter 2

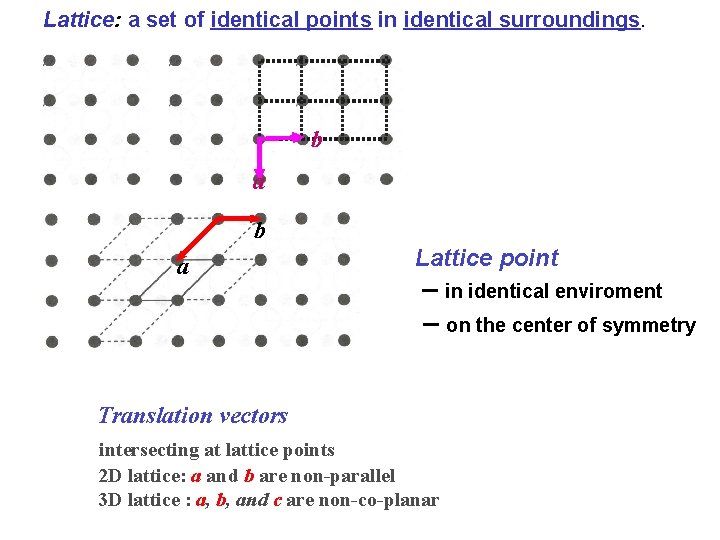
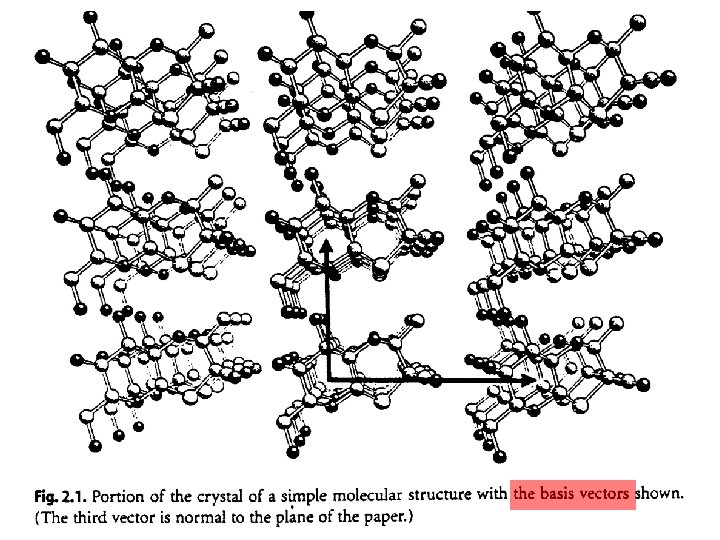
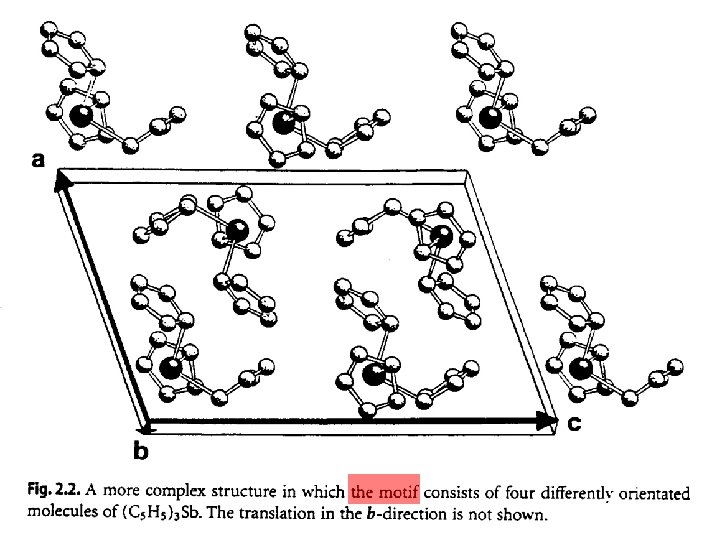
Lattice: a set of identical points in identical surroundings. b a Lattice point – in identical enviroment – on the center of symmetry Translation vectors intersecting at lattice points 2 D lattice: a and b are non-parallel 3 D lattice : a, b, and c are non-co-planar

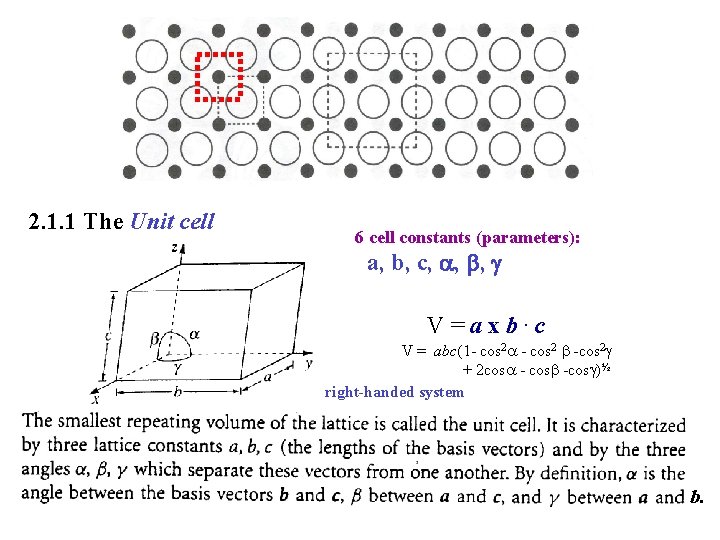
2. 1. 1 The Unit cell 6 cell constants (parameters): a, b, c, , , V=axb. c V = abc(1 - cos 2 -cos 2 + 2 cos -cos )½ right-handed system b.

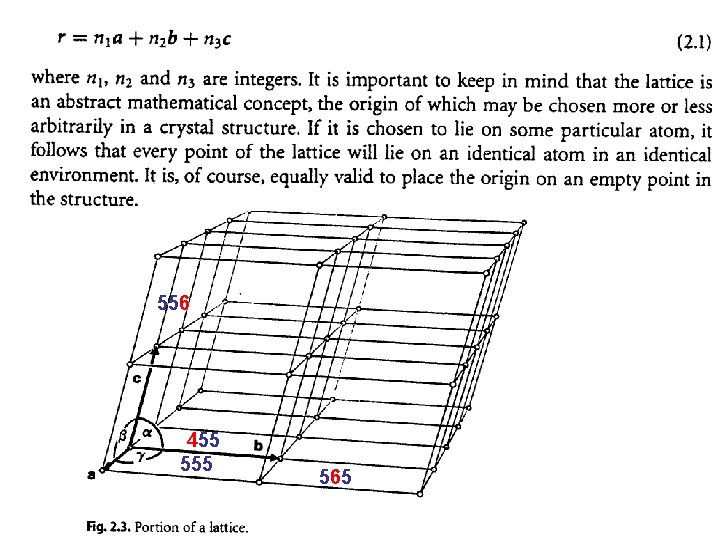
556 455 565

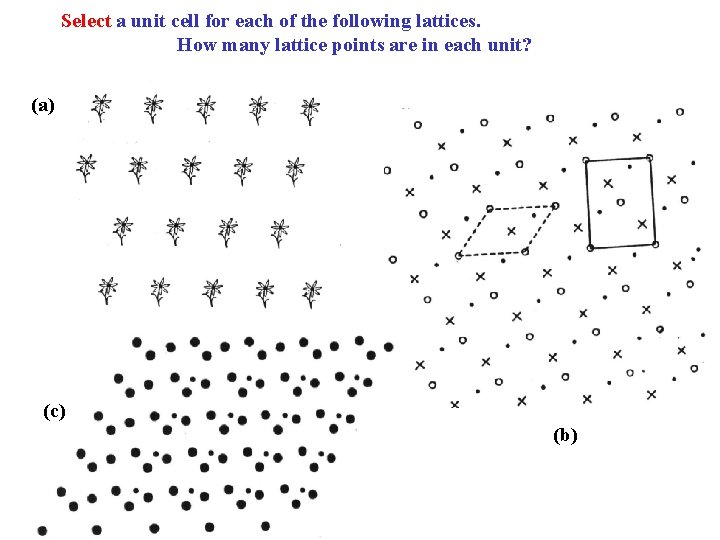
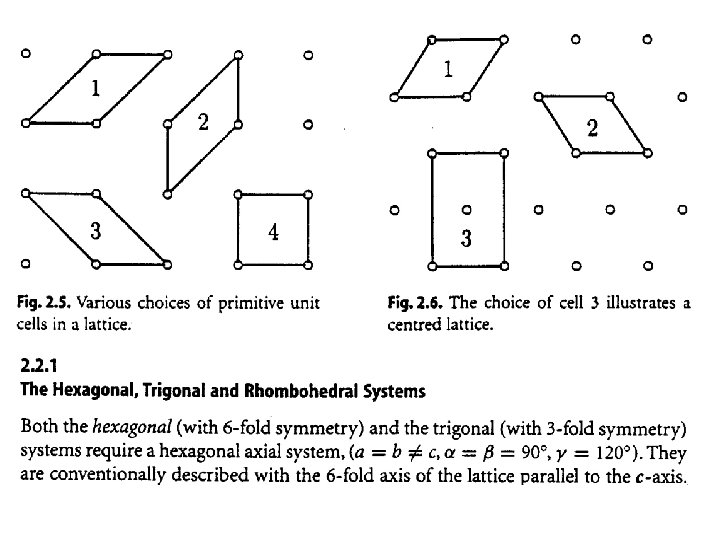
Select a unit cell for each of the following lattices. How many lattice points are in each unit? (a) (c) (b)

1 x 0 1 y 0 1 z 0

Crystal Symmetry-Three simple symmetry elements i, m, n (i) inversion center i (x, y, z) (-x, -y, -z) (ii) mirror plane m (x, y, z) (x, y, -z) … (iii) rotation axes n, where n = 360 o/α (α= angle of rotation) (x, y, z) (-x, -y, z) … 180 o Horizontally clockwise rotation All two-dimensional lattices have two-fold rotation axis.

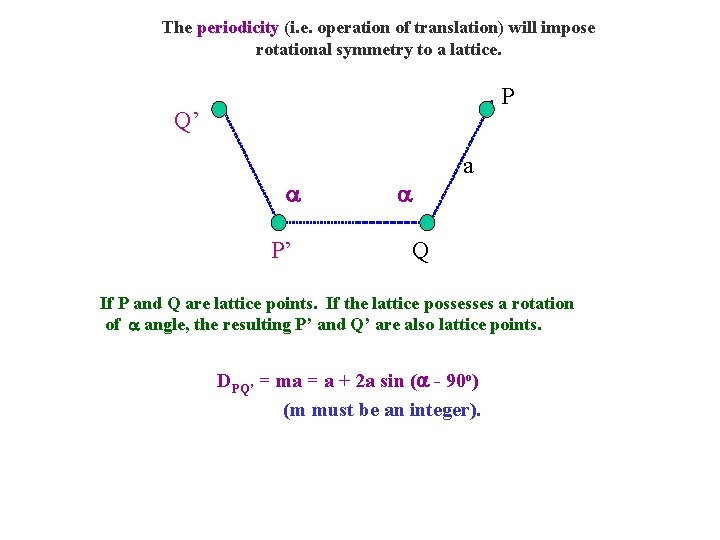
The periodicity (i. e. operation of translation) will impose rotational symmetry to a lattice. P Q’ P’ a Q If P and Q are lattice points. If the lattice possesses a rotation of angle, the resulting P’ and Q’ are also lattice points. DPQ’ = ma = a + 2 a sin ( - 90 o) (m must be an integer).

DPQ’ = ma = a + 2 a sin ( - 90 o) (m must be an integer). After rearrangement, cos = (m-1)/2 m must fall in the range of 3 to -1: m 3 2 1 0 -1 360 o 90 o 120 o 180 o n-fold rotation 1 6 4 3 2 (one-fold) (six-fold) (four-fold) (three-fold) (two-fold) In all 2 D and 3 D lattices, only five kinds of rotation angles are allowed.

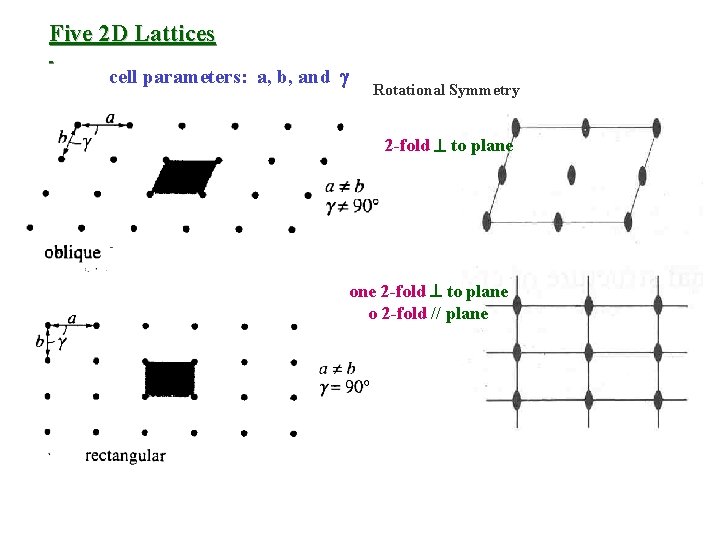
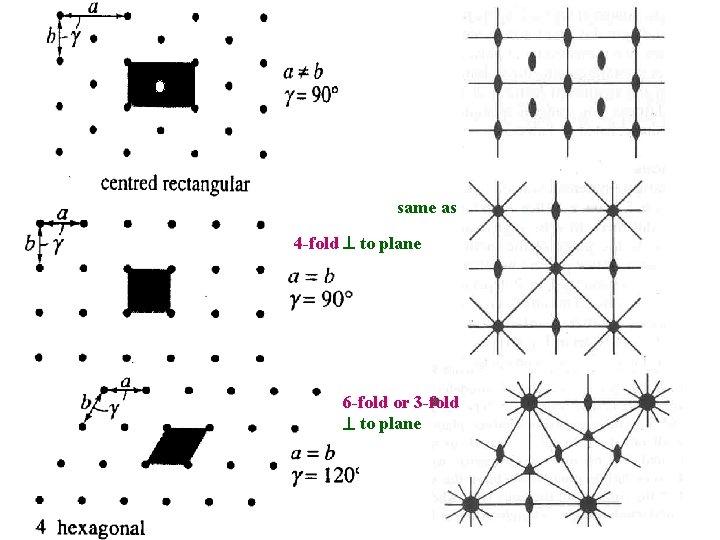
Five 2 D Lattices cell parameters: a, b, and Rotational Symmetry 2 -fold to plane one 2 -fold to plane two 2 -fold // plane

same as above 4 -fold to plane 6 -fold or 3 -fold to plane

The Seven Crystal Systems: cell parameters: a, b, c, , , no. independent parameters. 6 4 3 2 1 * 2 2 The symbol implies that equality is not required by symmetry. *In hexagonal lattice. If in rhombohedral lattice: a = b = c; = = 90 o

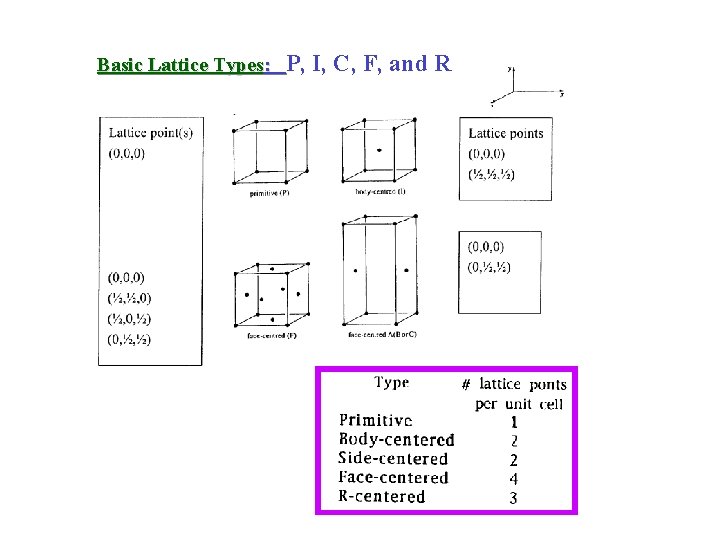
Basic Lattice Types: P, I, C, F, and R

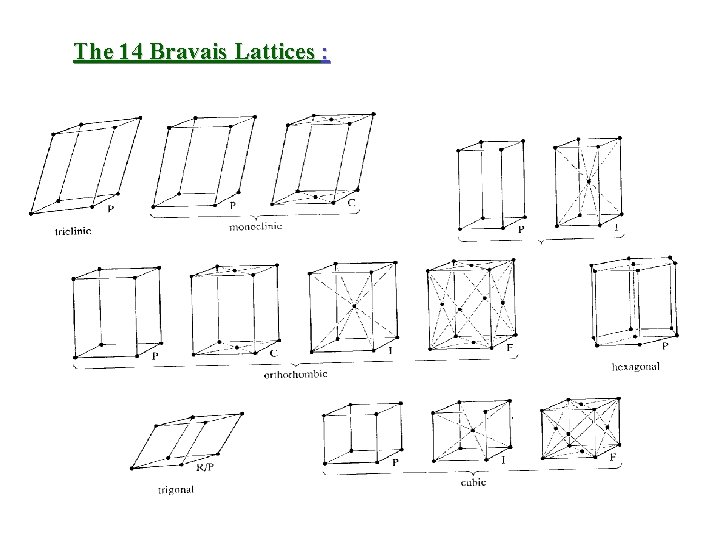
The 14 Bravais Lattices :

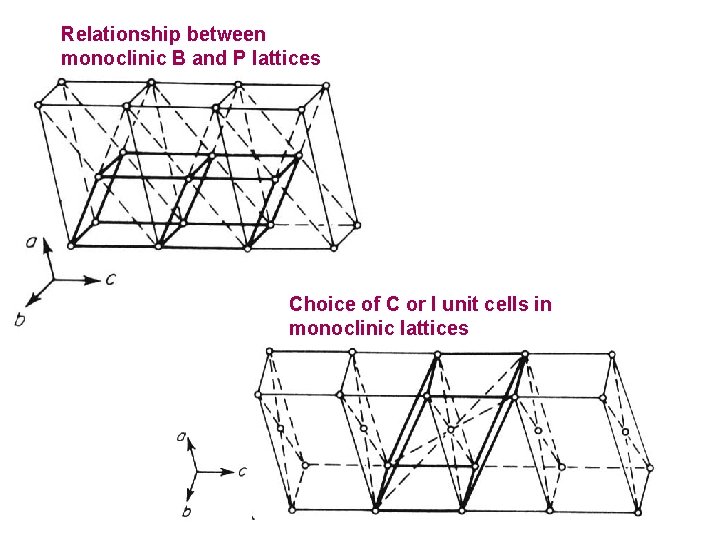
Relationship between monoclinic B and P lattices Choice of C or I unit cells in monoclinic lattices

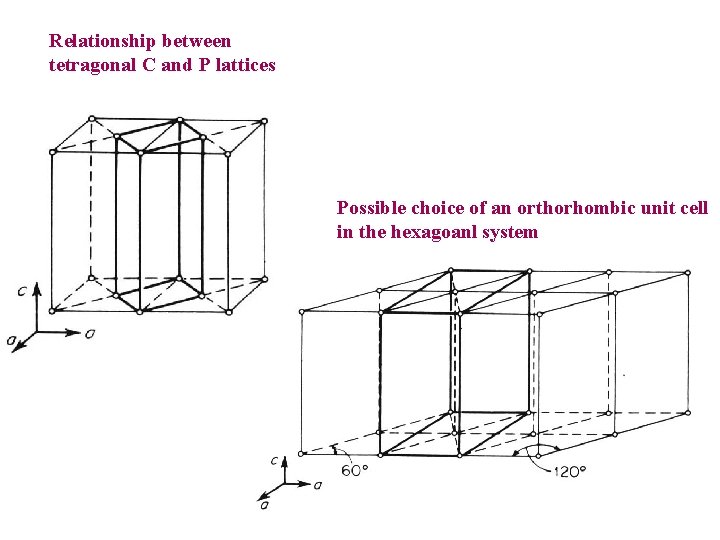
Relationship between tetragonal C and P lattices Possible choice of an orthorhombic unit cell in the hexagoanl system

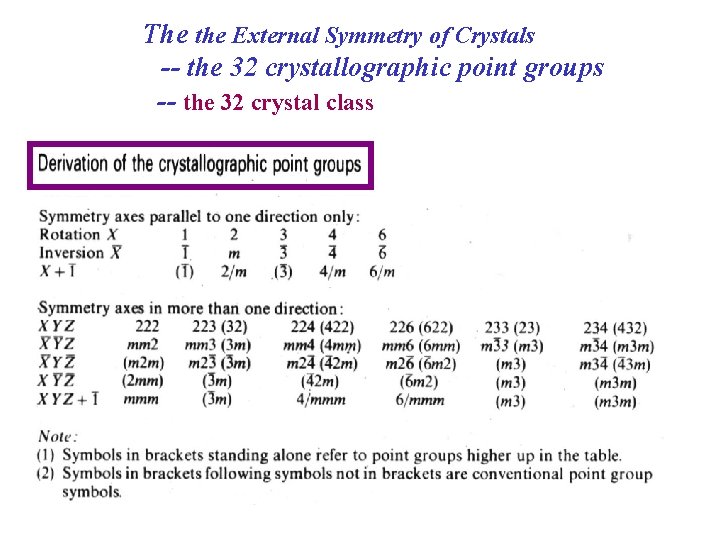
Ten basic symmetry elements in crystals (i) Combination of simple symmetry elements of inversion and rotation 1 2 3 4 6 1 2 3 i m 4 6 They also represent ten point groups. (ii) Combination of symmetry axes – when two rotation axes are combined a third rotation axis is created. There are only six possible combinations of rotation axes of symmetry that can operate on crystal lattice. 222 223 224 226 233 234

The the External Symmetry of Crystals -- the 32 crystallographic point groups -- the 32 crystal class

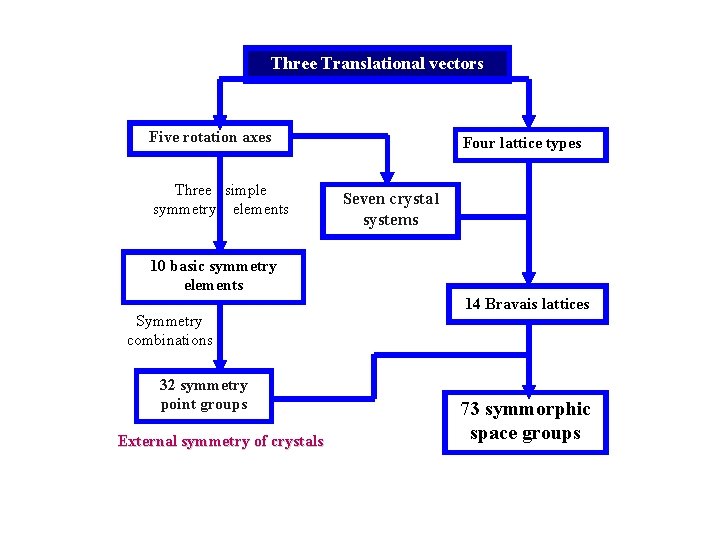
Three Translational vectors Five rotation axes Three simple symmetry elements Four lattice types Seven crystal systems 10 basic symmetry elements Symmetry combinations 32 symmetry point groups External symmetry of crystals 14 Bravais lattices 73 symmorphic space groups