Chapter 1 Introduction What is an algorithm b

Chapter 1 Introduction
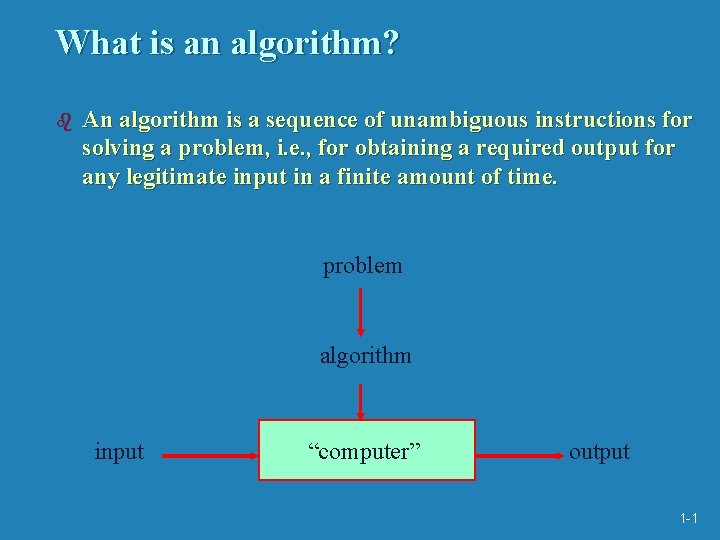
What is an algorithm? b An algorithm is a sequence of unambiguous instructions for solving a problem, i. e. , for obtaining a required output for any legitimate input in a finite amount of time. problem algorithm input “computer” output 1 -1

What is an algorithm? b Recipe, process, method, technique, procedure, routine, … with following requirements: 1. Finiteness b terminates after a finite number of steps 2. Definiteness b rigorously and unambiguously specified 3. Input b valid inputs are clearly specified 4. Output b can be proved to produce the correct output given a valid input 5. Effectiveness b steps are sufficiently simple and basic 1 -2

Why study algorithms? b Theoretical importance • the core of computer science b Practical importance • A practitioner’s toolkit of known algorithms • Framework for designing and analyzing algorithms for new problems 1 -3

Two main issues related to algorithms b How to design algorithms b How to analyze algorithm efficiency 1 -4

Analysis of algorithms b How good is the algorithm? • time efficiency • space efficiency b Does there exist a better algorithm? • lower bounds • optimality 1 -5

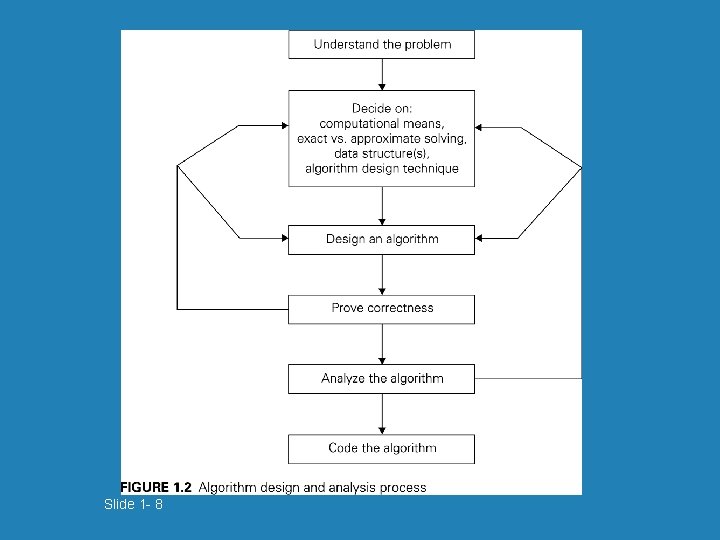
Basic Issues Related to Algorithms b How to design algorithms b How to express algorithms b Proving correctness b Efficiency • Theoretical analysis • Empirical analysis b Optimality 1 -6

Analysis of Algorithms b How good is the algorithm? • Correctness • Time efficiency • Space efficiency b Does there exist a better algorithm? • Lower bounds • Optimality 1 -7
Slide 1 - 8

Euclid’s Algorithm Problem: Find gcd(m, n), the greatest common divisor of two nonnegative, not both zero integers m and n Examples: gcd(60, 24) = 12, gcd(60, 0) = 60, gcd(0, 0) = ? Euclid’s algorithm is based on repeated application of equality gcd(m, n) = gcd(n, m mod n) until the second number becomes 0, which makes the problem trivial. Example: gcd(60, 24) = gcd(24, 12) = gcd(12, 0) = 12 1 -9

Two descriptions of Euclid’s algorithm Step 1 Step 2 Step 3 If n = 0, return m and stop; otherwise go to Step 2 Divide m by n and assign the value fo the remainder to r Assign the value of n to m and the value of r to n. Go to Step 1. while n ≠ 0 do r ← m mod n m← n n←r return m 1 -10

Other methods for computing gcd(m, n) Consecutive integer checking algorithm Step 1 Assign the value of min{m, n} to t Step 2 Divide m by t. If the remainder is 0, go to Step 3; otherwise, go to Step 4 Step 3 Divide n by t. If the remainder is 0, return t and stop; otherwise, go to Step 4 Decrease t by 1 and go to Step 2 1 -11
![Other methods for gcd(m, n) [cont. ] Middle-school procedure Step 1 Step 2 Step Other methods for gcd(m, n) [cont. ] Middle-school procedure Step 1 Step 2 Step](http://slidetodoc.com/presentation_image_h2/5121cc2f5f683285d47bd961092426a3/image-13.jpg)
Other methods for gcd(m, n) [cont. ] Middle-school procedure Step 1 Step 2 Step 3 Step 4 Find the prime factorization of m Find the prime factorization of n Find all the common prime factors Compute the product of all the common prime factors and return it as gcd(m, n) 1 -12

Algorithm design techniques/strategies b Brute force b Greedy approach b Divide and conquer b Dynamic programming b Decrease and conquer b Iterative improvement b Transform and conquer b Backtracking b Space and time tradeoffs b Branch and bound 1 -13

Computational Problem b A computational (or algorithmic) problem is specified by a precise definition of • the legal inputs • the required outputs as a function of those inputs 1 -14

Example of computational problem: sorting b Statement of problem: • Input: A sequence of n numbers <a 1, a 2, …, an> • Output: A reordering of the input sequence <a´ 1, a´ 2, …, a´n> so that a´i ≤ a´j whenever i < j b Instance: The sequence <5, 3, 2, 8, 3> b Algorithms: • • Selection sort Insertion sort Merge sort (many others) 1 -15
![Selection Sort b Input: array a[1], …, a[n] b Output: array a sorted in Selection Sort b Input: array a[1], …, a[n] b Output: array a sorted in](http://slidetodoc.com/presentation_image_h2/5121cc2f5f683285d47bd961092426a3/image-17.jpg)
Selection Sort b Input: array a[1], …, a[n] b Output: array a sorted in non-decreasing order b Algorithm: for i=1 to n swap a[i] with smallest of a[i], …a[n] • see also pseudocode, section 3. 1 1 -16

Some Well-known Computational Problems b b b b b Sorting Searching Shortest paths in a graph Minimum spanning tree Primality testing Traveling salesman problem Knapsack problem Chess Towers of Hanoi Program termination 1 -17

Important problem types b sorting b searching b string processing b graph problems b combinatorial problems b geometric problems b numerical problems 1 -18

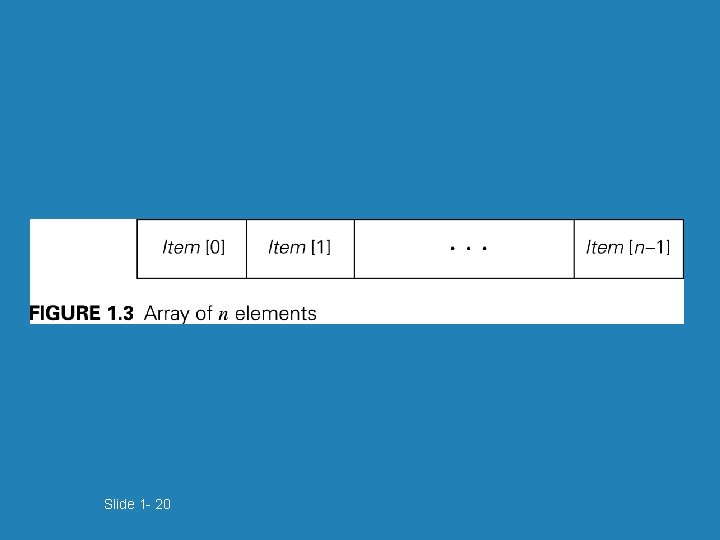
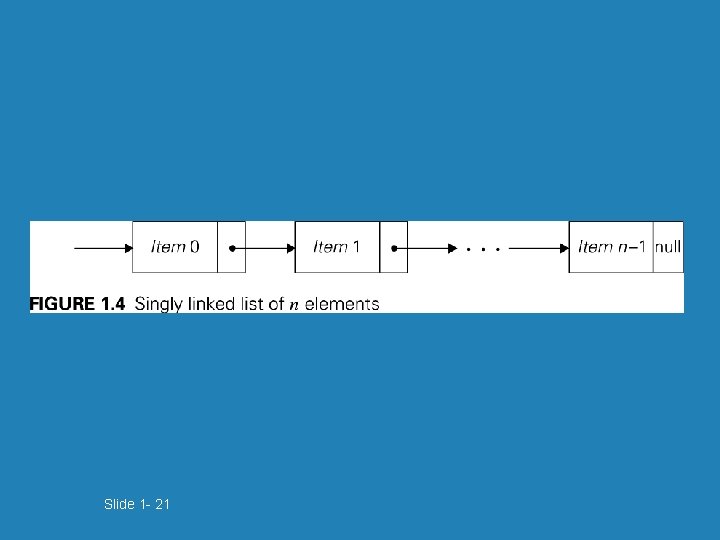
Fundamental data structures b list b graph • array b tree • linked list b set and dictionary • string b stack b queue b priority queue 1 -19
Slide 1 - 20
Slide 1 - 21
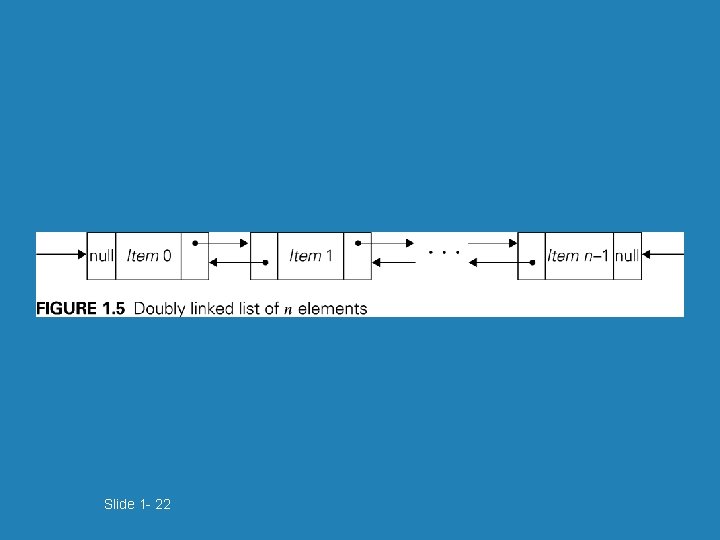
Slide 1 - 22
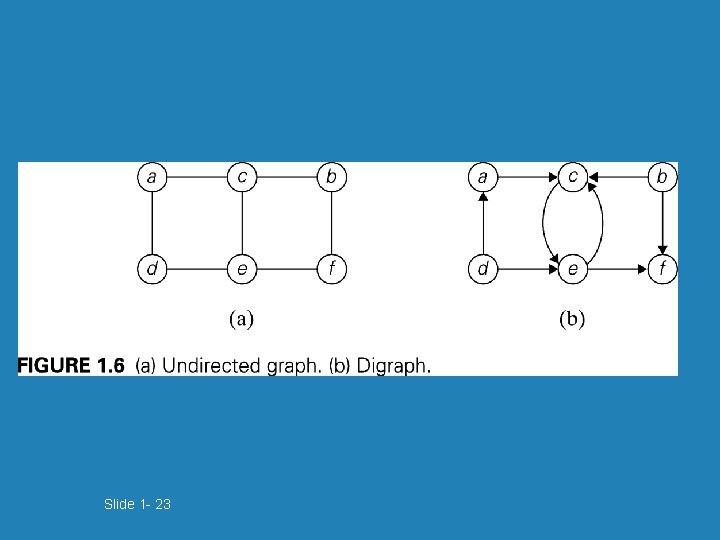
Slide 1 - 23

Slide 1 - 24
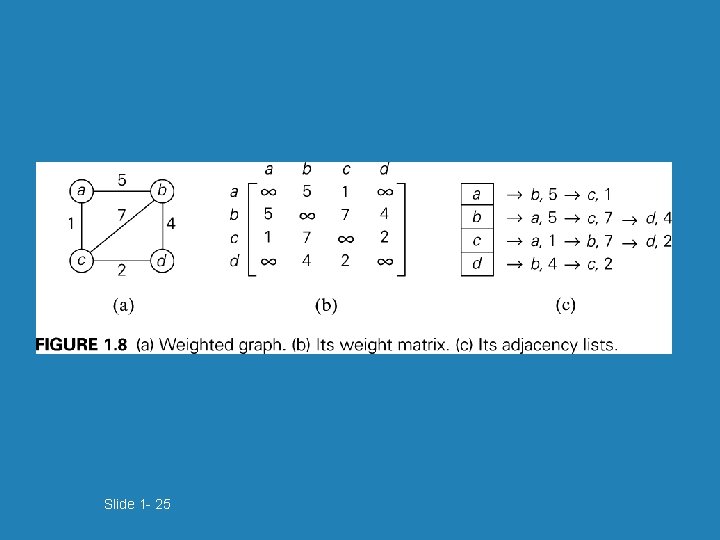
Slide 1 - 25
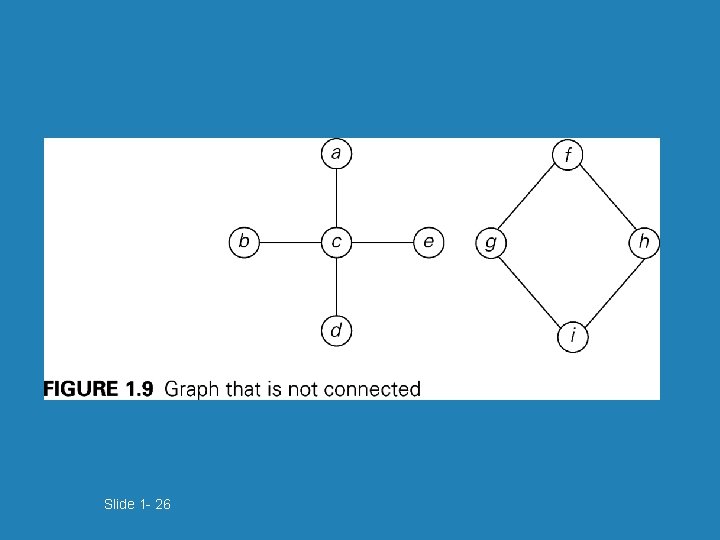
Slide 1 - 26
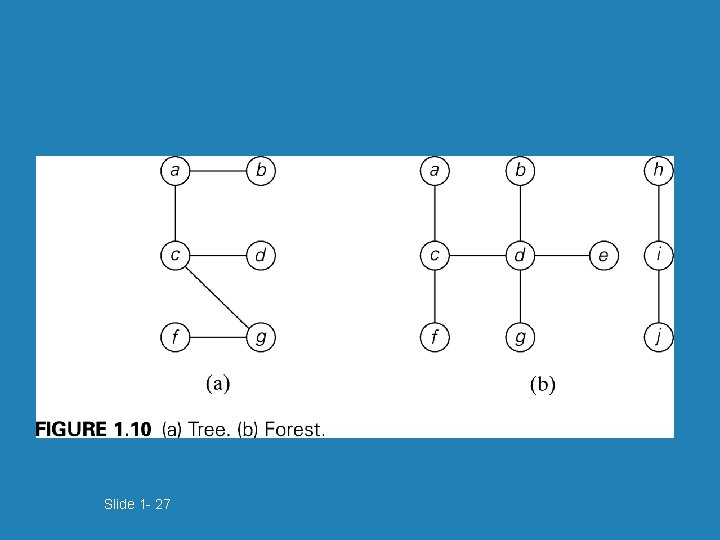
Slide 1 - 27
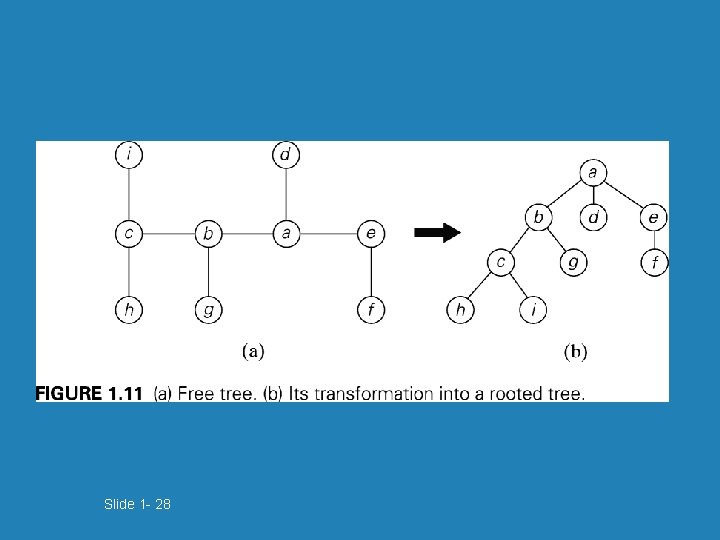
Slide 1 - 28
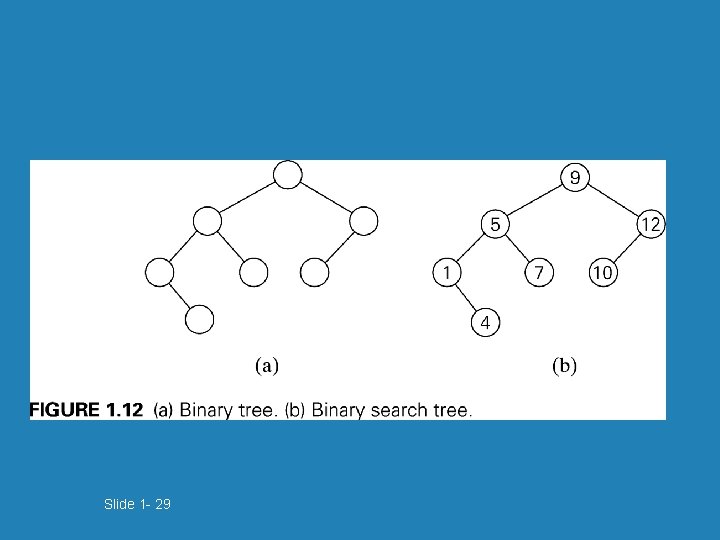
Slide 1 - 29
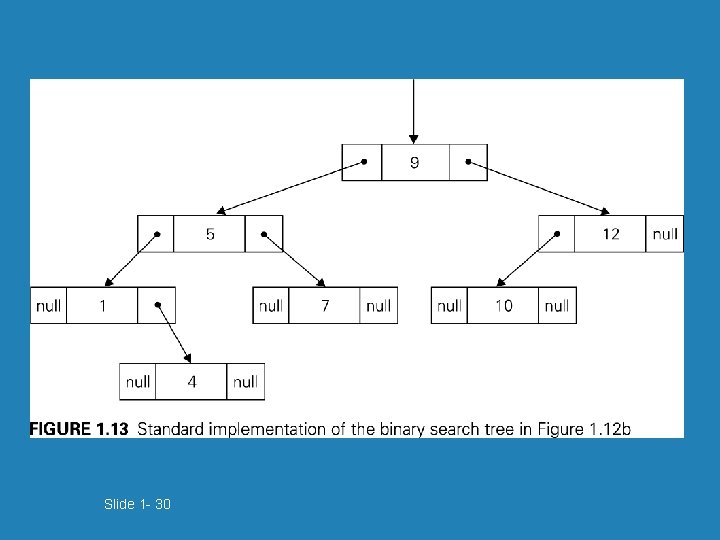
Slide 1 - 30
Slide 1 - 31
- Slides: 32