Chapter 1 Introduction to Science Section 3 Organizing

Chapter 1: Introduction to Science Section 3: Organizing Data

Objectives • After completing the lesson, students will be able to. . . ▫ Interpret line graphs, bar graphs, and pie graphs; ▫ Identify the significant figures in calculations; ▫ Use scientific notation and significant figures in problem solving; ▫ Understand the difference between precision and accuracy.

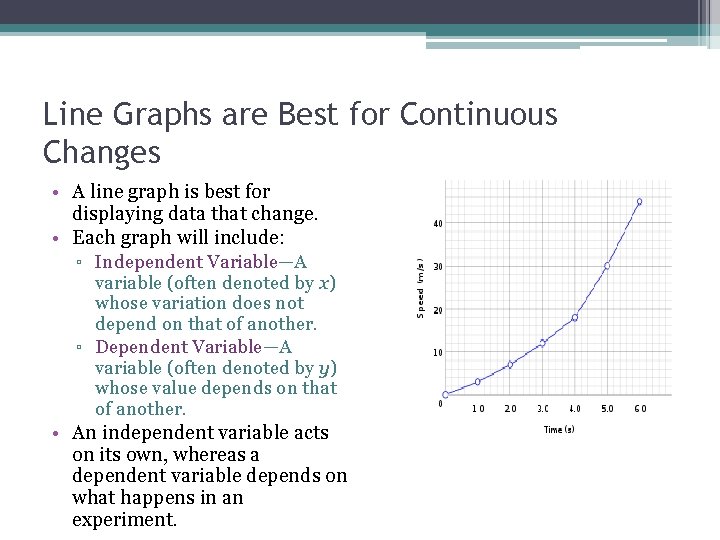
Line Graphs are Best for Continuous Changes • A line graph is best for displaying data that change. • Each graph will include: ▫ Independent Variable—A variable (often denoted by x) whose variation does not depend on that of another. ▫ Dependent Variable—A variable (often denoted by y) whose value depends on that of another. • An independent variable acts on its own, whereas a dependent variable depends on what happens in an experiment.

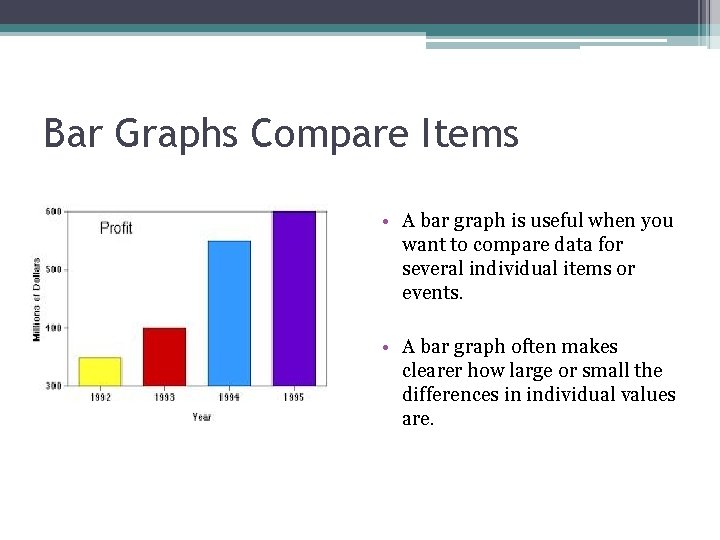
Bar Graphs Compare Items • A bar graph is useful when you want to compare data for several individual items or events. • A bar graph often makes clearer how large or small the differences in individual values are.

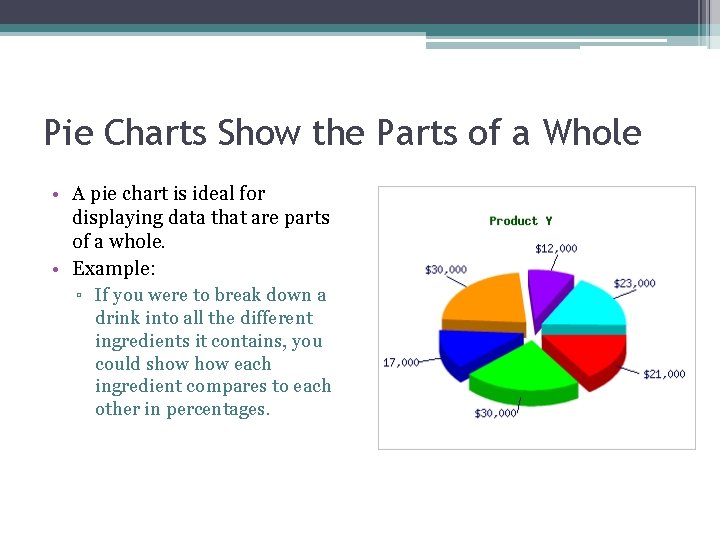
Pie Charts Show the Parts of a Whole • A pie chart is ideal for displaying data that are parts of a whole. • Example: ▫ If you were to break down a drink into all the different ingredients it contains, you could show each ingredient compares to each other in percentages.

Scientific Notation • Scientists sometimes need to express measurements using numbers that are very large or very small. • To reduce the amount of numbers into a smaller figure, scientists adopted the method of scientific notation. • Scientific Notation—A value written as a simple number multiplied by a power of 10. • Examples: ▫ 10⁴ = 10, 000 ▫ 10⁵ = 100, 000 ▫ 10° = 1 ▫ 10 -⁴ = 0. 0001 • When you move the decimal to the right side, you get 10 to the positive power. • When you move the decimal to the left, you get 10 to the negative power.

Using Scientific Notation • When you use scientific notation in calculations, you follow the rules of algebra for powers of 10. • When you multiply two values in scientific notation, you add the powers of 10. • When you divide, you subtract the powers of 10. • Example: ▫ 10⁸/ 10⁴ = 10⁴

Using Significant Figures • Precision—The degree of exactness of a measurement. • Significant Figures—The digits in a measurement that are known with certainty. • Accuracy—The extent to which a measurement approaches the true value. • When you use measurements in calculations, the answer is only as precise as the least precise measurement used in the calculation—the measurement with the fewest significant figures.

Summary • Representing scientific data with graphs helps you and others understand experimental results. • Scientific notation is useful for writing very large and very small measurements because it uses powers of 10 instead of strings of zeros. • Accuracy is the extent to which a value approaches the true value. • Precision is the degree of exactness of a measurement. • Expressing data with significant figures tells others how precisely a measurement was made.