Chapter 1 Introduction to Clustering Section 1 1

Chapter 1 Introduction to Clustering

Section 1. 1 Introduction

Objectives n n n 3 Introduce clustering and unsupervised learning. Explain the various forms of cluster analysis. Outline several key distance metrics used as estimates of experimental unit similarity.

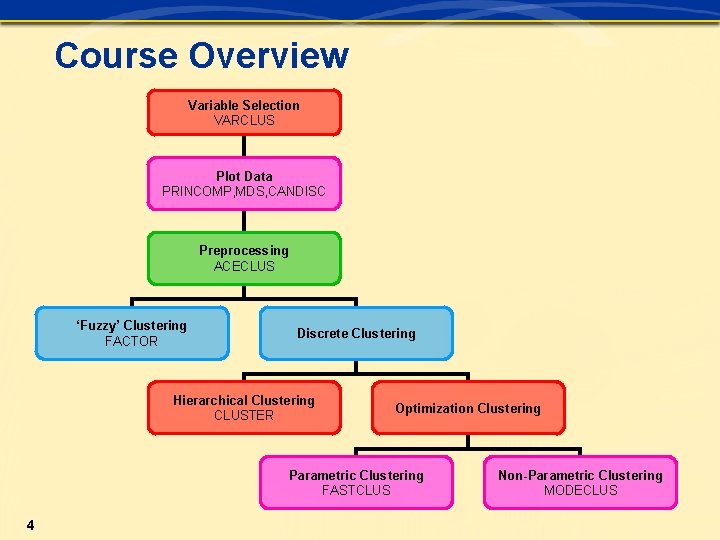
Course Overview Variable Selection VARCLUS Plot Data PRINCOMP, MDS, CANDISC Preprocessing ACECLUS ‘Fuzzy’ Clustering FACTOR Discrete Clustering Hierarchical Clustering CLUSTER Optimization Clustering Parametric Clustering FASTCLUS 4 Non-Parametric Clustering MODECLUS

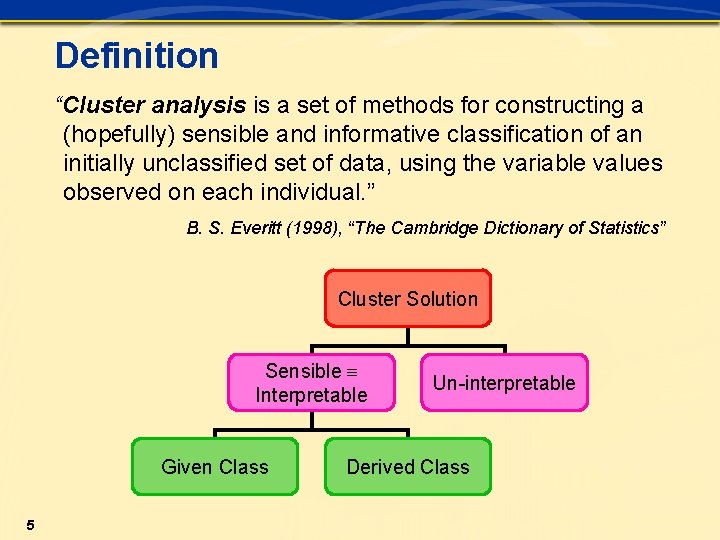
Definition “Cluster analysis is a set of methods for constructing a (hopefully) sensible and informative classification of an initially unclassified set of data, using the variable values observed on each individual. ” B. S. Everitt (1998), “The Cambridge Dictionary of Statistics” Cluster Solution Sensible Interpretable Given Class 5 Un-interpretable Derived Class

Unsupervised Learning without a priori knowledge about the classification of samples; learning without a teacher. Kohonen (1995), “Self-Organizing Maps” 6

Section 1. 2 Types of Clustering

Objectives n Distinguish between the two major classes of clustering methods: – hierarchical clustering – optimization (partitive) clustering. 8

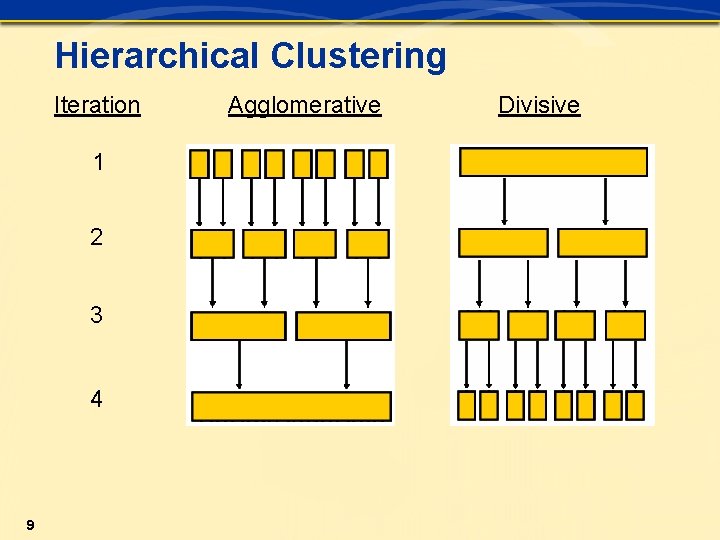
Hierarchical Clustering Iteration 1 2 3 4 9 Agglomerative Divisive

Propagation of Errors Iteration 1 10 2 (error) 3 (error) 4 (error)

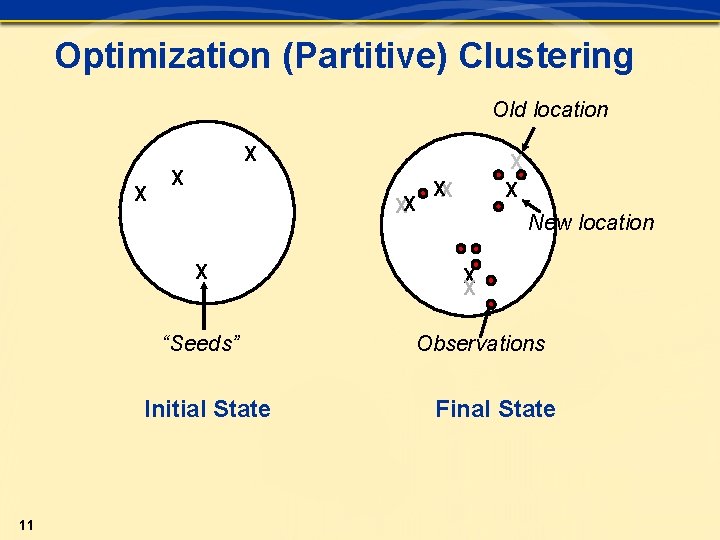
Optimization (Partitive) Clustering Old location X XX X “Seeds” Initial State 11 X X XX New location X X Observations Final State

Heuristic Search 1. Find an initial partition of the n objects into g groups. 2. Calculate the change in the error function produced by moving each observation from its own cluster to another group. 3. Make the change resulting in the greatest improvement in the error function. 4. Repeat steps 2 and 3 until no move results in improvement. 12

Section 1. 3 Similarity Metrics

Objectives n n 14 Define similarity and what comprises a good measure of similarity. Describe a variety of similarity metrics.

What Is Similarity? Although the concept of similarity is fundamental to our thinking, it is also often difficult to precisely quantify. Which is more similar to a duck: a crow or a penguin? The metric that you choose to operationalize similarity (for example, Euclidean distance or Pearson correlation) often impacts the clusters you recover. 15

What Makes a Good Similarity Metric? The following principles have been identified as a foundation of any good similarity metric: 1. symmetry: d(x, y) = d(y, x) 2. non-identical distinguishability: if d(x, y) 0 then x y 3. identical non-distinguishability: if d(x, y) = 0 then x = y Some popular similarity metrics (for example, correlation) fail to meet one or more of these criteria. 16

Euclidean Distance Similarity Metric Pythagorean Theorem: The square of the hypotenuse is equal to the sum of the squares of the other two sides. (x 1, x 2) x 2 (0, 0) 17 x 1

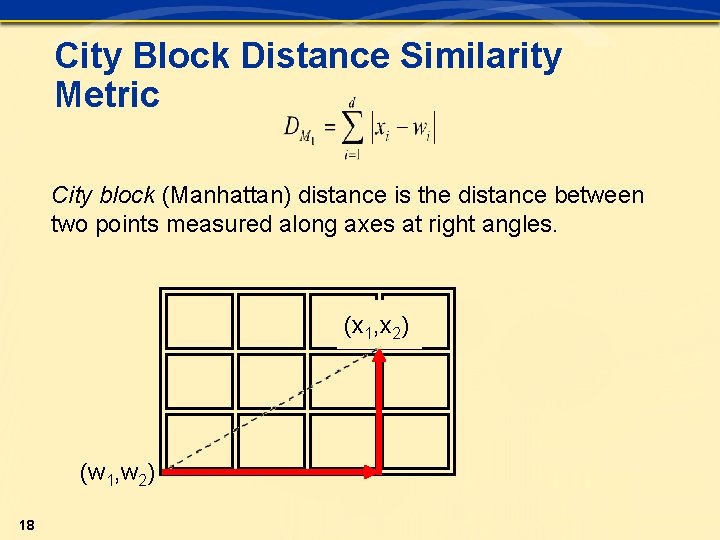
City Block Distance Similarity Metric City block (Manhattan) distance is the distance between two points measured along axes at right angles. (x 1, x 2) (w 1, w 2) 18

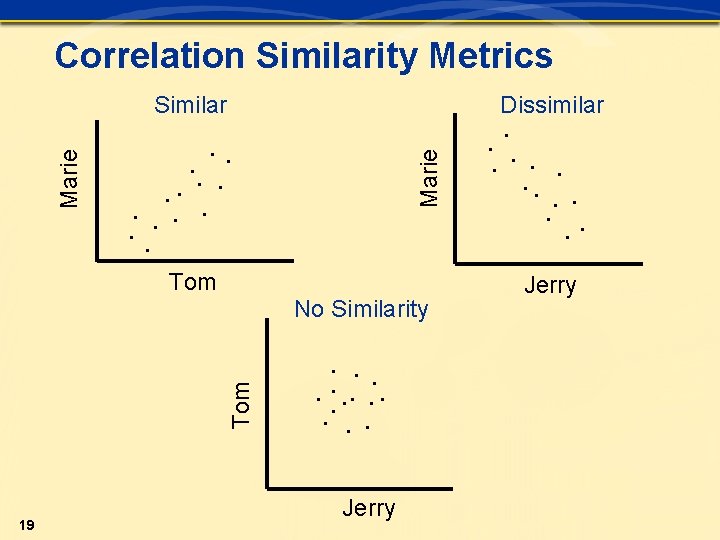
Correlation Similarity Metrics Dissimilar Marie Tom No Similarity 19 . . . Jerry . . . Similar Jerry

The Problem with Correlation Variable Observation 1 x 2 x 3 x 4 x 5 Mean Std. Dev. 5 4 3 2 1 3 1. 5811 Observation 2 51 42 33 24 15 33 14. 2302 The correlation between observations 1 and 2 is a perfect 1. 0, but are the observations really similar? 20

Density Estimate Based Similarity Metrics Clusters can be seen as areas of increased observation density. Similarity is a function of the distance between the identified density bubbles (hyper-spheres). similarity Density Estimate 1 (Cluster 1) 21 Density Estimate 2 (Cluster 2)

Hamming Distance Similarity Metric 1 2 3 4 5 … 17 22 Gene A 0 0 1 Gene B 0 1 1 0 0 1 1 1 0 0 0 1 1 1 0 1 1 1

The DISTANCE Procedure General form of the DISTANCE procedure: PROC DISTANCE METHOD=method <options> ; COPY variables; VAR level (variables < / option-list >) ; RUN; Both the PROC DISTANCE statement and the VAR statement are required. 23

Generating Distances ch 1 s 3 d 1 This demonstration illustrates the impact on cluster formation of two distance metrics generated by the DISTANCE procedure. 24

Section 1. 4 Classification Performance

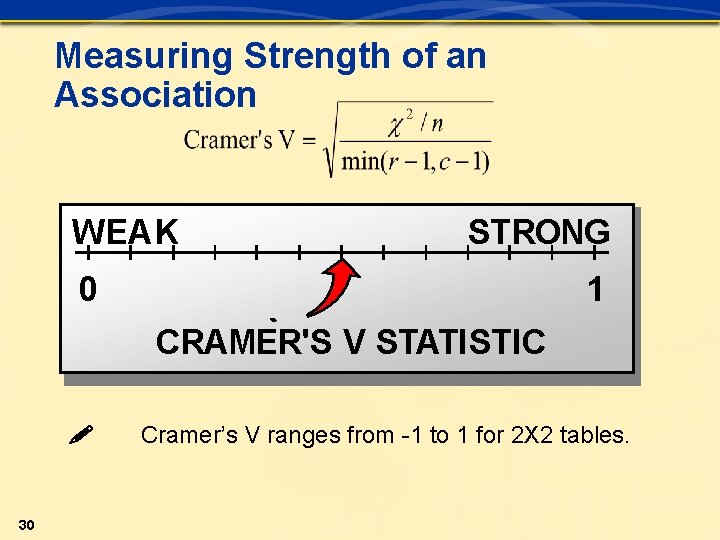
Objectives n n 26 Use classification matrices to determine the quality of a proposed cluster solution. Use the chi-square and Cramer’s V statistic to assess the relative strength of the derived association.

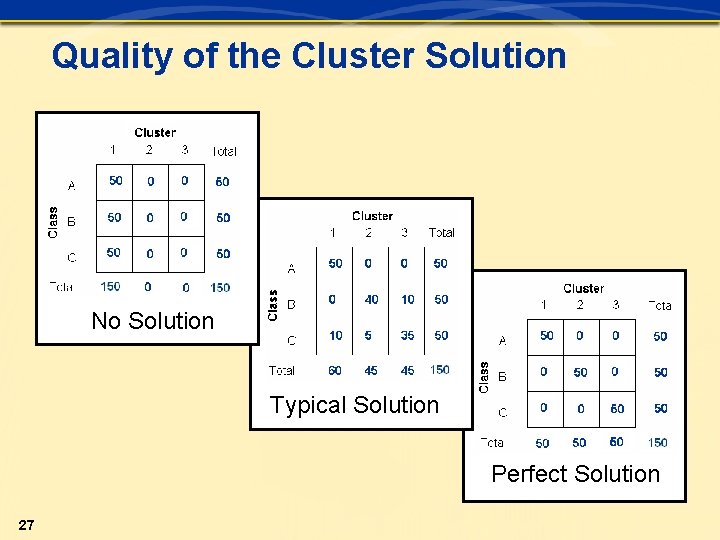
Quality of the Cluster Solution No Solution Typical Solution Perfect Solution 27

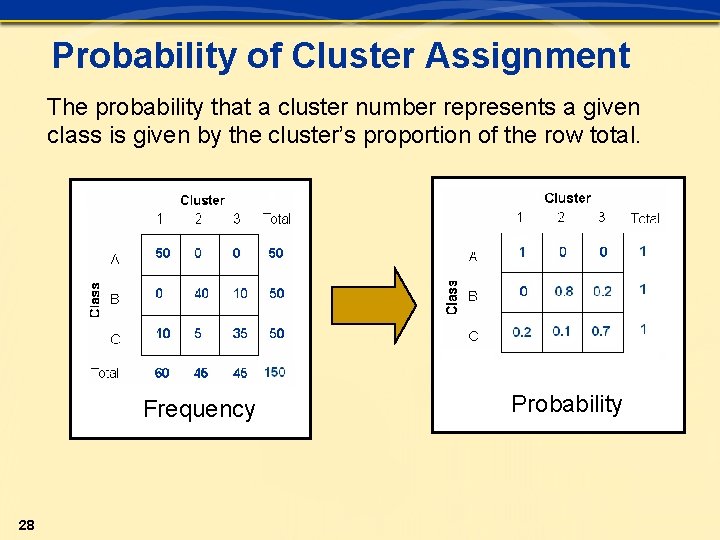
Probability of Cluster Assignment The probability that a cluster number represents a given class is given by the cluster’s proportion of the row total. Frequency 28 Probability

The Chi-Square Statistic The chi-square statistic (and associated probability) • determine whether an association exists • depend on sample size • do not measure the strength of the association. 29

Measuring Strength of an Association WEAK STRONG 0 1 CRAMER'S V STATISTIC 30 Cramer’s V ranges from -1 to 1 for 2 X 2 tables.