Chapter 1 Introduction The solutions of engineering problems

Chapter 1 Introduction • The solutions of engineering problems can be obtained using analytical methods or numerical methods. • Analytical differentiation and integration provide a closedform derivative and integral, respectively, only for simple functions. • Very often analytical solutions cannot be obtained. • Numerical methods can be used where analytical methods are not capable of or practical for providing solutions. 1

The procedure for solving a problem 1. 2. 3. 4. 5. Identify the problem State the objectives Develop alternative solutions Evaluate the alternatives Implement the best alternative 2

Analytical VS Numerical Analysis • To find minimum of • Analytical: after differentiate 2 x-3 the minimum solution occurs at x = 1. 5 • Numerical: define the interval from 1 to 2 increment of 0. 2, min falls in 1. 4 < x < 1. 6 To improve the accuracy, we can search in 1. 4 < x < 1. 6 with a small increment, such as 0. 04. 3

Analytical VS Numerical Analysis • Analytical techniques provide a direct solution and will result in exact solution if one exists. • Analytical methods are practical only for functions that have a simple, closed-form mathematical structure. • Numerical methods can be used with any function. They often require many iterations to get the true solution. • The numerical solution usually is not exact, and it is also necessary to provide initial estimates of the unknowns. 4

Taylor Series Taylor series where is the remainder. or First-order approximation Second-order approximation Third-order approximation 5

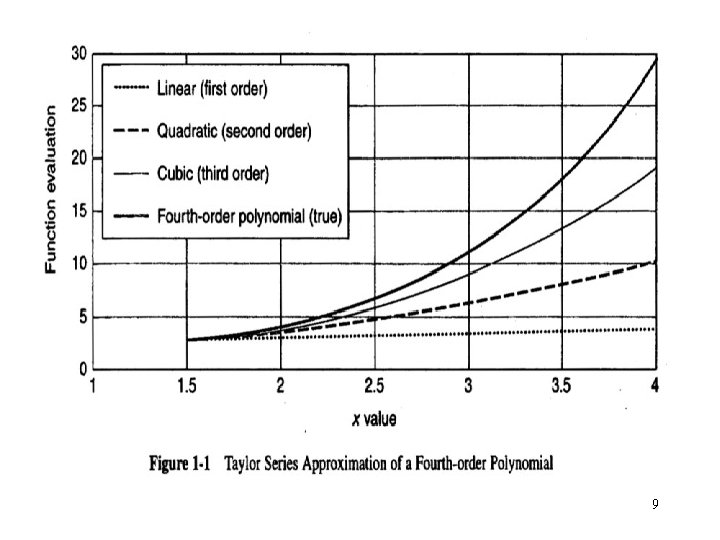
Taylor Series Expansion • The importance of the individual terms of the Taylor series depends on the nature of the function and the distance h. The higher-order terms become more important as the nonlinearity of the function increases and the difference h = increases. • If the function is linear, only the term with the first derivative is necessary. • The error increases as fewer terms of the Taylor series are included. 6

Example: Nonlinear Polynomials 4 th-order polynomial For a base point x 0= 1. 0 distance h = 0. 5 7

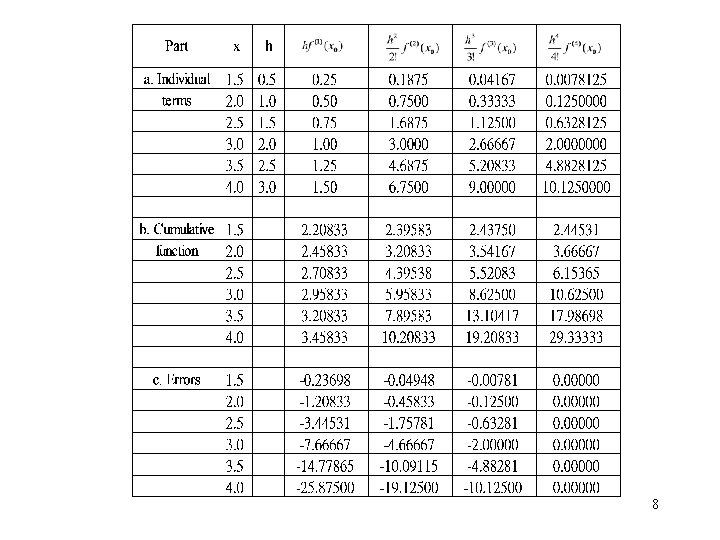
8

9

Taylor Series Expansion of the Square Root The square-root function can be expressed as For a base point x 0 = 1 and h = 0. 001 10

Example Taylor Series 11

Example Taylor Series 12