Chapter 1 Introduction Levitin Introduction to The Design

Chapter 1 Introduction Levitin: Introduction to The Design and Analysis of Algorithms

Why study algorithms? b Theoretical importance • the core of computer science b Practical importance • A practitioner’s toolkit of known algorithms • Framework for designing and analyzing algorithms for new problems 1 -1

Two main issues related to algorithms b How to design algorithms b How to analyze algorithm efficiency 1 -2

What is an algorithm? An algorithm is a sequence of unambiguous instructions for solving a problem, i. e. , for obtaining a required output for any legitimate input in a finite amount of time. problem algorithm input “computer” output 1 -3

What is an algorithm? b 1. Recipe, process, method, technique, procedure, routine, … with following requirements: Finiteness b terminates after a finite number of steps 2. Definiteness b rigorously and unambiguously specified 3. Input b valid inputs are clearly specified 4. Output b can be proved to produce the correct output given a valid input 5. Effectiveness b steps are sufficiently simple and basic 1 -4

Alternative definition b An algorithm is a well-ordered collection of unambiguous and effectively computable operations that, when executed, produces a result and halts in a finite amount of time. b An algorithm is a sequence of unambiguous instructions for solving a problem, i. e. , for obtaining a required output for any legitimate input in a finite amount of time. b Muhammad ibn Musa al-Khwarizmi – 9 th century mathematician www. lib. virginia. edu/science/parshall/khwariz. html 1 -5

Historical Perspective b Euclid’s algorithm for finding the greatest common divisor • third century BC b What are alternative ways we can compute the gcd of two integers? 1 -6

Euclid’s Algorithm Problem: Find gcd(m, n), the greatest common divisor of two nonnegative, not both zero integers m and n Examples: gcd(60, 24) = 12, gcd(60, 0) = 60, gcd(0, 0) = ? Euclid’s algorithm is based on repeated application of equality gcd(m, n) = gcd(n, m mod n) until the second number becomes 0, which makes the problem trivial. Example: gcd(60, 24) = gcd(24, 12) = gcd(12, 0) = 12 1 -7

Two descriptions of Euclid’s algorithm Step 1 Step 2 Step 3 If n = 0, return m and stop; otherwise go to Step 2 Divide m by n and assign the value fo the remainder to r Assign the value of n to m and the value of r to n. Go to Step 1. while n ≠ 0 do r ← m mod n m← n n←r return m 1 -8

Other methods for computing gcd(m, n) Consecutive integer checking algorithm Step 1 Assign the value of min{m, n} to t Step 2 Divide m by t. If the remainder is 0, go to Step 3; otherwise, go to Step 4 Step 3 Divide n by t. If the remainder is 0, return t and stop; otherwise, go to Step 4 Decrease t by 1 and go to Step 2 1 -9

Other methods for gcd(m, n) [cont. ] Middle-school procedure Step 1 Step 2 Step 3 Step 4 Find the prime factorization of m Find the prime factorization of n Find all the common prime factors Compute the product of all the common prime factors and return it as gcd(m, n) Is this an algorithm? 1 -10

Sieve of Eratosthenes Input: Integer n ≥ 2 Output: List of primes less than or equal to n for p ← 2 to n do A[p] ← p for p ← 2 to n do if A[p] 0 //p hasn’t been previously eliminated from the list j ← p* p while j ≤ n do A[j] ← 0 //mark element as eliminated j←j+p Example: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1 -11

Basic Issues Related to Algorithms b How to design algorithms b How to express algorithms b Proving correctness b Efficiency • Theoretical analysis • Empirical analysis b Optimality 1 -12

1. 2 Fundamentals of Algorithmic Problem Solving b Algorithms are procedural solutions to problems b Steps for designing and analyzing an algorithm • Understand the problem • Ascertain the capabilities of a computational device • Choose between exact and approximate problem solving • Decide on appropriate data structures 1 -13

Fundamentals of Algorithmic Problem Solving, continued: Algorithm design techniques/strategies b Brute force b Greedy approach b Divide and conquer b Dynamic programming b Decrease and conquer b Iterative improvement b Transform and conquer b Backtracking b Space and time tradeoffs b Branch and bound 1 -14

Fundamentals of Algorithmic Problem Solving continued b Methods of specifying an algorithm • Present: pseudocode • Earlier: flowchart b Proving an algorithm’s correctness • • Mathematical induction for recursion Modus ponens E. g. algorithm stops since number gets smaller on each iteration Approximation algorithms are more difficult 1 -15

Fundamentals of Algorithmic Problem Solving, continued: Analysis of Algorithms and Coding b How good is the algorithm? • Correctness • Time efficiency • Space efficiency b Does there exist a better algorithm? • Lower bounds • Optimality b Algorithm ultimately implemented as a computer program • Success depends on above considerations 1 -16

1. 3 Important problem types b sorting b searching b string processing b graph problems b combinatorial problems b geometric problems b numerical problems 1 -17

Example of computational problem: sorting b Statement of problem: • Input: A sequence of n numbers <a 1, a 2, …, an> • Output: A reordering of the input sequence <a´ 1, a´ 2, …, a´n> so that a´i ≤ a´j whenever i < j b Instance: The sequence <5, 3, 2, 8, 3> b Algorithms: • • Selection sort Insertion sort Merge sort (many others) 1 -18

Selection Sort b Input: array a[1], …, a[n] b Output: array a sorted in non-decreasing order b Algorithm: for i=1 to n swap a[i] with smallest of a[i], …a[n] • see also pseudocode, section 3. 1 1 -19

Fundamental data structures b list b graph • array b tree • linked list b set and dictionary • string b stack b queue b priority queue 1 -20

Data Structure b Definition: • “A particular scheme of organizing related data items. ” • Example: – Array – String – List • Classified into – – Linear Graphs Tree Abstract 1 -21

Linear Structures b b Array String (Type of Mathematical Sequence) • Character, Binary, Bit… b Linked List • Nodes, Head, Tail • Singly Linked, Doubly Linked, b Stack • LIFO, Top, Push, Pop b Queue • FIFO, Front, Rear/End, Enqueue, Dequeue 1 -22

Graphs b Graph – • Def: “A graph G = <V, E> is defined by a pair of two sets: a finite set V of items called vertices and a set E of pairs (2 -tuples) of vertices that represent the edges between the vertices. • Undirected, Directed (digraph) • Loops • Complete, Sparse, Dense 1 -23

Representing Graphs b Graphs – • Inherently abstract • Directed or Undirected • Two common representations: – Adjacency matrix int P[][] = new int P[][]; – Adjacency linked list – Linked. List<Edge> Q = new Linked. List<Edge>( ); A B C A 0 1 1 B 1 1 0 C 0 0 1 { (A, B), (A, C), (B, A), (B, B), (C, C) } 24

Weighted Graphs b Weighted Graph – • A graph G, with the added property that the edges between nodes is assigned a “weight” • Edge weight may represent: cost, distance, time… A B A 0 1. 5 2. 3 B 1. 3 2. 0 0 C 1. 1 { (A, B, 1. 5), (A, C, 2. 3), (B, A, 1. 3), (B, B, 2. 0), (C, C, 1. 1) } 25

Graph Terms (1/2) b Path – • A path from vertex u and v of a graph G exists if there exists a set adjacent edges that starts with u and ends with v b Simple – • The path contains only unique edges (no duplicates) b Length of a path – • The number of edges in the aforementioned set 26

Graph Terms (2/2) b b Connected – • iff, for every pair of its vertices, <u, v>, there is a path from u to v. Connected Components – • If a graph is not connected, it is made of two or more connected components. • The “maximal” connected subgraph of a given graph. Cycle – • A simple path, of non-zero length, that starts & ends at the same vertex. Acyclic Graph – • A graph with no cycles 27

Trees b Tree • A connected acyclic graph • Properties – |E| = |V|-1 – For every two vertices, <u, v>, there exists exactly one simple path from u to v. b Forest • A set of trees • An acyclic graph that is not necessarily connected 28

Rooted Trees b Rooted Tree • A tree, with a “root” node • Root nodes are selected arbitrarily (any vertex) b Tree genealogy • • • Ancestors Children Siblings Parents Descendents Leaf nodes 29

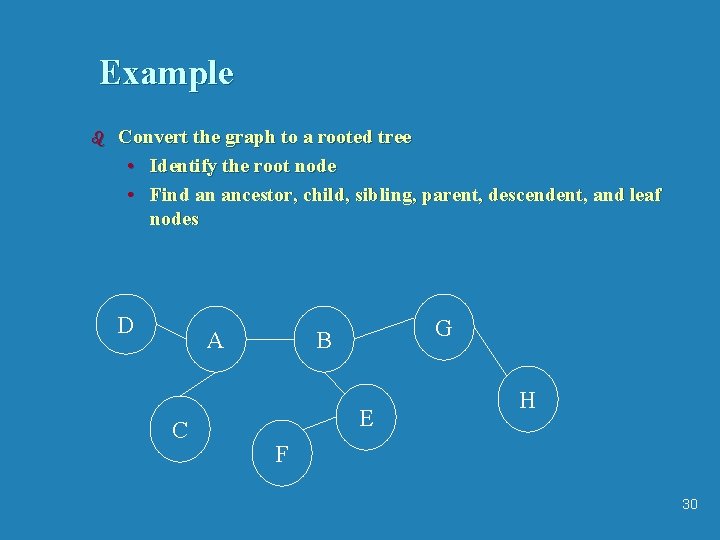
Example b Convert the graph to a rooted tree • Identify the root node • Find an ancestor, child, sibling, parent, descendent, and leaf nodes D A C G B E H F 30

Height & Depth of Trees b Depth • Depth of vertex v is the length of the simple path from the root to v • Count the edges b Height • Height of a tree is the length of the longest simple path from the root to the deepest leaf nodes 31

Binary Tree b Binary Tree • Simplest tree structure • Every node has the property: • “Left child” and “Right child” children. 32

Representing Trees b Linked Lists (ala LISP) (A (B X) (C X (D E)))) b Arrays (for defined n-ary) trees ABCBXCXXXXXDE b class tree. Node<Type> { Type data; Linked. List<Tree. Node<Type>> children; } 33

Graph Algorithm b Determine if a graph contains a “universal sink” • A graph with at least one node with an in-degree of |V|-1, and an out -degree of 0. 34