Chapter 1 Introduction Definition of Algorithm An algorithm

Chapter 1 Introduction Definition of Algorithm An algorithm is a finite sequence of precise instructions for performing a computation or for solving a problem. Example 1 Describe an algorithm for finding the maximum (largest) value in a finite sequence of integers. Solution 1. Set the temporary maximum equal to the first integer in the sequence. 2. Compare the next integer in the sequence to the temporary maximum, and set the larger one to be temporary maximum. 3. Repeat the previous step if there are more integers in the sequence. 4. Stop when there are no integers left in the sequence. The temporary maximum at this point is the maximum in the sequence. Instead of using a particular computer language, we use a form of pseudocode.

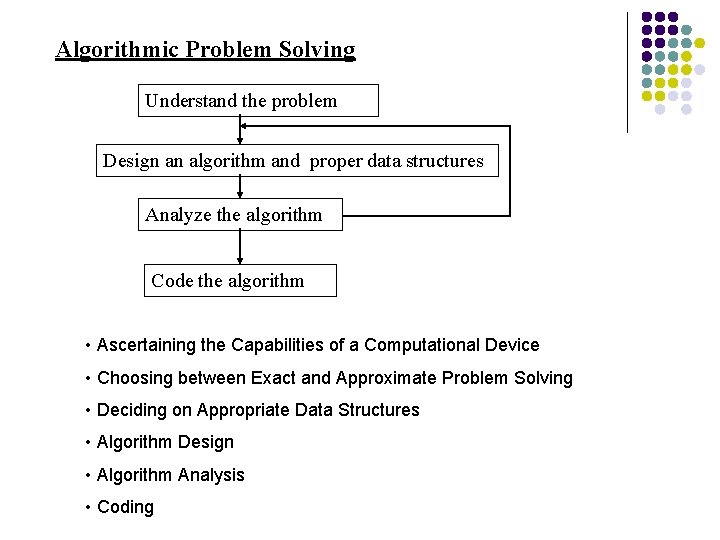
Algorithmic Problem Solving Understand the problem Design an algorithm and proper data structures Analyze the algorithm Code the algorithm • Ascertaining the Capabilities of a Computational Device • Choosing between Exact and Approximate Problem Solving • Deciding on Appropriate Data Structures • Algorithm Design • Algorithm Analysis • Coding

Important Problem Types • Sorting • Searching • String processing (e. g. string matching) • Graph problems (e. g. graph coloring problem) • Combinatorial problems (e. g. maximizes a cost) • Geometric problems (e. g. convex hull problem) • Numerical problems (e. g. solving equations )

Fundamental Data Structures 1. Array a[1] a[2] a[3] a[n] 2. Link List Head of list 10 3. Binary Tree 6 4 1 9 7 17 13 4 9 20

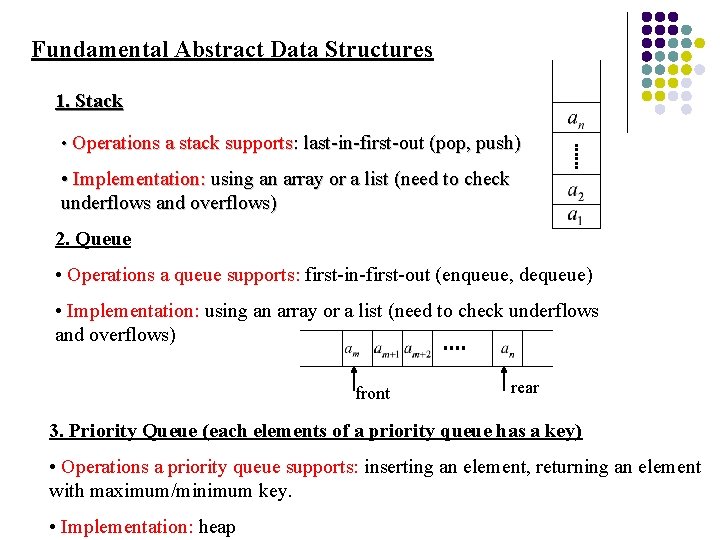
Fundamental Abstract Data Structures 1. Stack • Operations a stack supports: last-in-first-out (pop, push) • Implementation: using an array or a list (need to check underflows and overflows) 2. Queue • Operations a queue supports: first-in-first-out (enqueue, dequeue) • Implementation: using an array or a list (need to check underflows and overflows) front rear 3. Priority Queue (each elements of a priority queue has a key) • Operations a priority queue supports: inserting an element, returning an element with maximum/minimum key. • Implementation: heap

Assignment (1) Read the sections of the text book about array, linked list, stack, queue, heap and priority queue. (2) (i) Implement stack S and queue Q using both of array and linked list. (ii) Write a main function to do the following operations for S: pop, push 10 times, pop, repeat push and pop 7 times. Do the following operations for Q: dequeue, enqueue 10 times, dequeue, depueue, repeat enqueue and dequeue 7 times. When you use array, declare the size of the array to be 10. Printout all the elements in S and in Q.

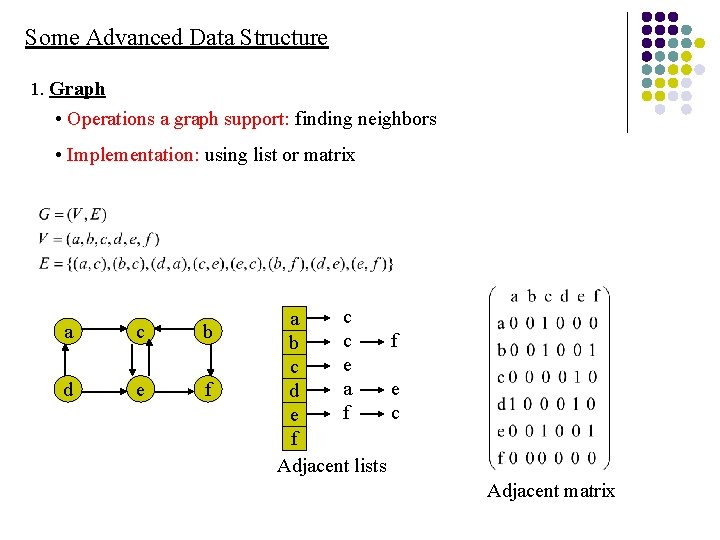
Some Advanced Data Structure 1. Graph • Operations a graph support: finding neighbors • Implementation: using list or matrix a c b d e f c a c f b e c a e d f c e f Adjacent lists Adjacent matrix

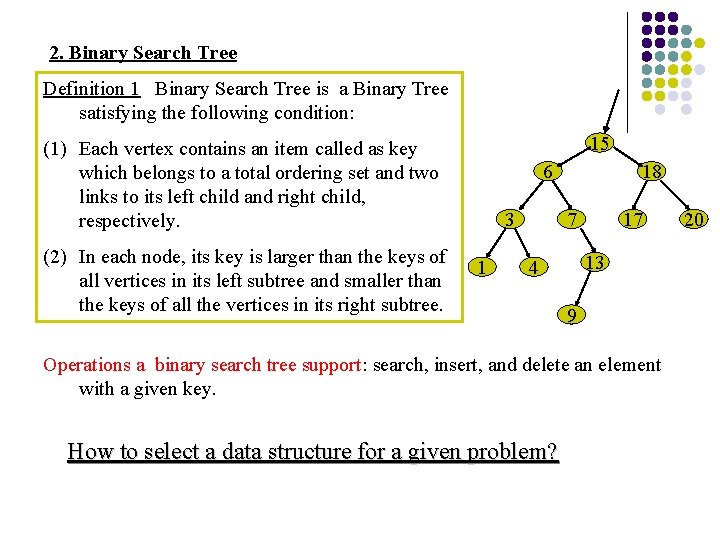
2. Binary Search Tree Definition 1 Binary Search Tree is a Binary Tree satisfying the following condition: 15 (1) Each vertex contains an item called as key which belongs to a total ordering set and two links to its left child and right child, respectively. (2) In each node, its key is larger than the keys of all vertices in its left subtree and smaller than the keys of all the vertices in its right subtree. 6 3 1 18 7 17 13 4 9 Operations a binary search tree support: search, insert, and delete an element with a given key. How to select a data structure for a given problem? 20

Example: Select a data structure for supporting Dynamic Dictionary Definition 2 A Dynamic Dictionary is a data structure of item with keys that support the following basic operations: (1) Insert a new item (2) Remove an item with a given key (3) Search an item with a given key What data structure is the best?

Chapter 2 Fundamentals of the Analysis of Algorithm Implementation and Empirical Analysis Challenge in empirical analysis: • Develop a correct and complete implementation. • Determine the nature of the input data and other factors influencing on the experiment. Typically, There are three choices: actual data, random data, or perverse data. • Compare implementations independent to programmers, machines, compilers, or other related systems. • Consider performance characteristics of algorithms, especially for those whose running time is big. Can we analyze algorithms that haven’t run yet?

Example 1 Describe an algorithm for finding an element x in a list of distinct elements

Linear Search and Binary Search written in C++ 1. 2. Linear search int lsearch(int a[], int v, int l, int r) { for (int i=l; i<=n; i++) if (v==a[i]) return i; return -1; } Binary search int bsearch(int a[], int v, int l, int n) { while (r>=l) {int m=(l+r)/2; if (v==a[m]) return m; if (v<a[m]) r=m-1; else l=m+1; } return -1; }

Complexity of Algorithms Assume that both algorithms A and B solve the problem P. Which one is better? • Time complexity: the time required to solve a problem of a specified size. • Space complexity: the computer memory required to solve a problem of a specified size. The time complexity is expressed in terms of the number of operations used by the algorithm. • Worst case analysis: the largest number of operations needed to solve the given problem using this algorithm. • Average case analysis: the average number of operations used to solve the problem over all inputs.

Example 2 Analyze the time complexities of linear search algorithm and binary search algorithm 1 2(n+1) n 2 3 n+5

1 1 2 2 Number of operations = 4 log n+4 2

Orders of Growth Running time for a problem with size Running Time necessary operations instant 1 second 11. 5 days Never end days instant Instant 1 second Never end days Operation Per second Using silicon computer, no matter how fast CPU will be you can never solve the problem whose running time is exponential !!!

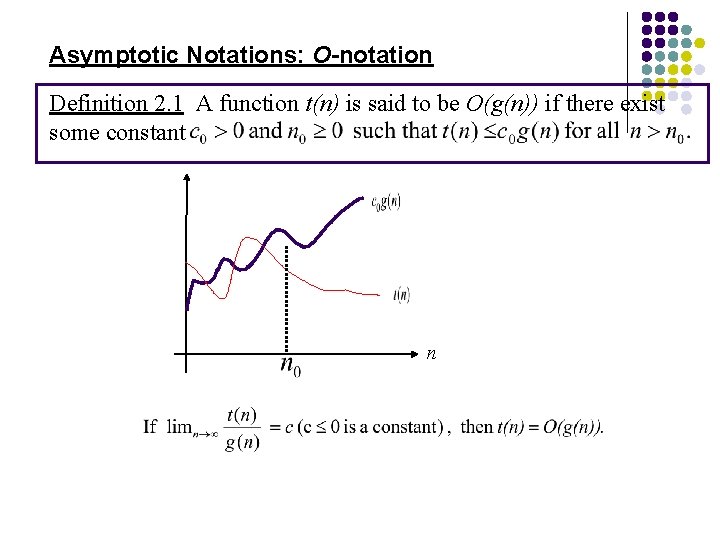
Asymptotic Notations: O-notation Definition 2. 1 A function t(n) is said to be O(g(n)) if there exist some constant n

Example 3 Prove 2 n+1=O(n) Example 5 List the following function in O-notation in increasing order:

Asymptotic Analysis of algorithms (using O-notation) Example 7 Analyze the time complexities of linear search algorithm and binary search algorithm asymptotically. Totally(addition): O(n)

Totally(comparison): O(log n)

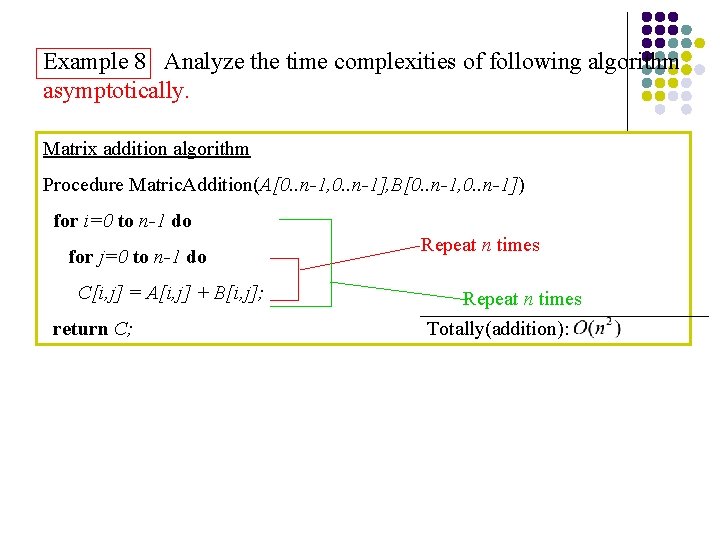
Example 8 Analyze the time complexities of following algorithm asymptotically. Matrix addition algorithm Procedure Matric. Addition(A[0. . n-1, 0. . n-1], B[0. . n-1, 0. . n-1]) for i=0 to n-1 do for j=0 to n-1 do C[i, j] = A[i, j] + B[i, j]; return C; Repeat n times Totally(addition):

Recursive Algorithms Example 9 Computing the factorial function F(n)=n!. F(n) can be defined recursively as follows: Factorial Algorithm Procedure factorial(n) Algorithm factorial calls itself in its body! if n = 0 return 1 else return factorial(n-1) * n; Time complexity(multiplication): T(0) = 0 T(n) = T(n-1) +1 when n>0 recurrence

Basic Recurrences Example 10 Solving the following recurrence T(0) = 1 T(n) = T(n-1) + 1 n>0 T(n) = T(n-1) + 1 = T(n-2) + 2 = T(n-3) + 1 + 2 = T(n-3) + 3 … = T(n-i) + i … = T(n-n) + n =n

Example 12 Solve the recurrence