Chapter 1 Introduction Chapter 2 Overview of Supervised

Chapter 1: Introduction Chapter 2: Overview of Supervised Learning 2006. 01. 20

Supervised learning n n n Training data set: several features and outcome Build a learner based on training data sets Predict the future unseen outcome from seen features of data 2

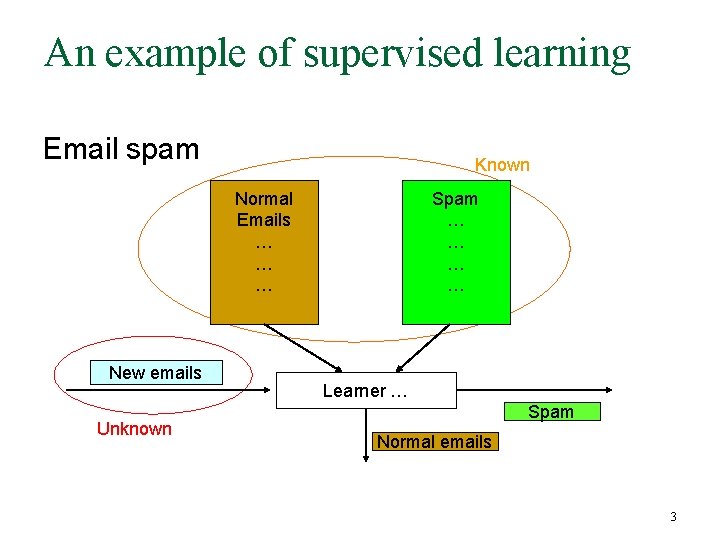
An example of supervised learning Email spam Known Normal Emails … … … New emails Unknown Spam … … Learner … Spam Normal emails 3

Input & Output n n Input = predictor = independent variable Output = response = dependent variable 4

Output Types n Quantitative >> regression q n Ex) stock price, temperature, age Qualitative >> classification q Ex) Yes/No, 5

Input Types n n n Quantitative Qualitative Ordered categorical q Ex) small, medium, big 6

Terminology n X : input q q q n Y : quantitative output q n Xj : j th component X : matrix xj : j th observed value ^ Y : prediction G : qualitative output 7

General model n Given input X, output Y unknown n Want to estimate the function f based on known data set (training data) 8

Two simple methods n Linear model, linear regression n Nearest neighbor method 9

Linear model n Give a vector of input features X = (X 1…Xp) Assume the linear relationship: n Least squares standard: n min -2 10

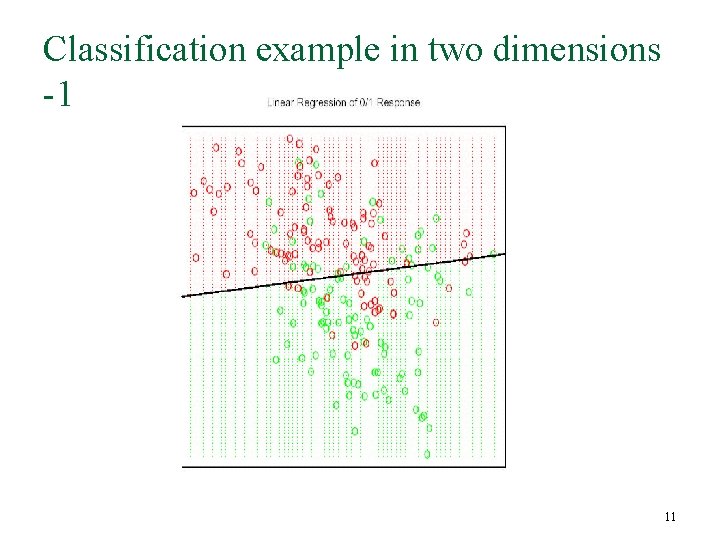
Classification example in two dimensions -1 11

Nearest neighbor method n Majority vote within the k nearest neighbors new K= 1: brown K= 3: green 12

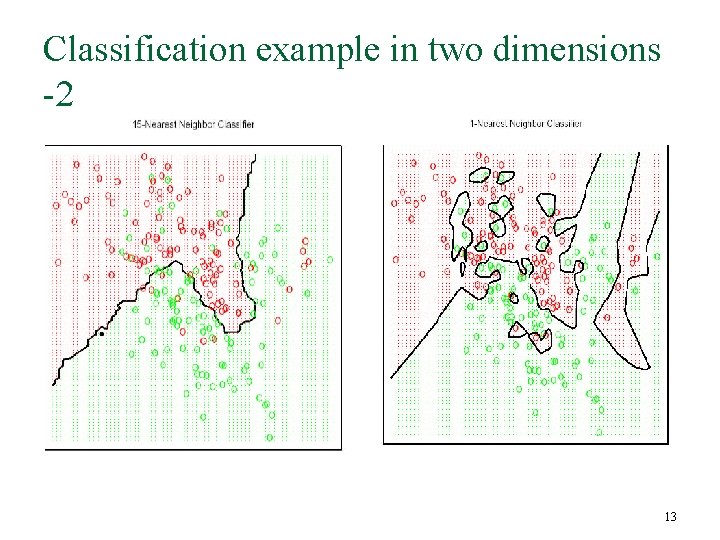
Classification example in two dimensions -2 13

Linear model vs. K-nearest neighbor n • • • Linear model #parameters: p Stable, smooth Low variance, high bias n • • • K-nearest neighbor #parameters: N/k Unstable, wiggly High variance, low bias Each method has its own situations for which it works best. 14

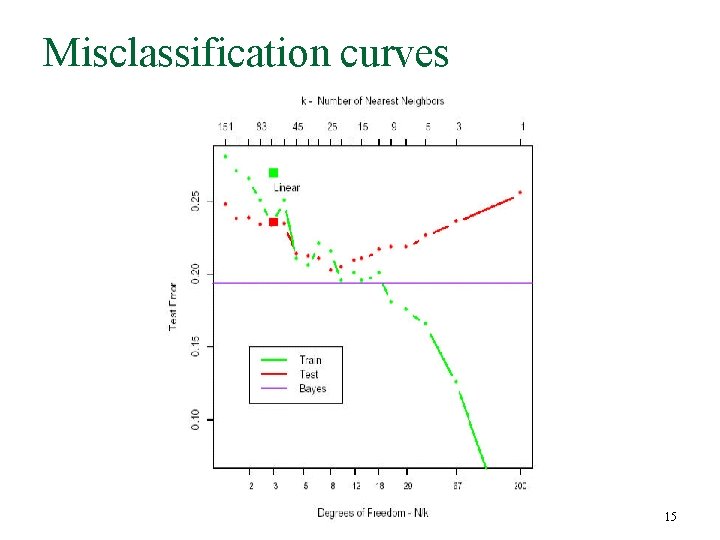
Misclassification curves 15

Enhanced Methods n n n Kernel methods using weights Modifying the distance kernels Locally weighted least squares Expansion of inputs for arbitrarily complex models Projection & neural network 16

Statistical decision theory (1) n Given input X in Rp, output Y in R Joint distribution: Pr(X, Y) Looking for predicting function: f(X) n Squared error loss: n n min EPE n Nearest-neighbor methods : ^ 17

Statistical decision theory (2) n k-Nearest neighbor n Linear model n If N, k , k/N 0 n But, the true function might not be linear! n Insufficient samples! Curse of dimensionality! 18

Statistical decision theory (3) n If ^ n n Robust But, discontinuous in their derivatives 19

Statistical decision theory (4) n G : categorical output variable L : Loss Function ^ EPE = E[L(G, G(X))] n Bayesian Classifier n n 20

References n Reading group on "elements of statistical learning” – overview. ppt q n Welcome to STAT 894 – Supervised. Learning. OVERVIEW 05. pdf q n http: //www. stat. ohio-state. edu/~goel/STATLEARN/ The Matrix Cookbook q n http: //sifaka. cs. uiuc. edu/taotao/stat. html http: //www 2. imm. dtu. dk/pubdb/views/ edoc_download. php/3274/pdf/imm 3274. pdf A First Course in Probability 21

2. 5 Local Methods in High Dimensions n n With a reasonably large set of training data, we could always approximate theoretically optimal conditional expectation by k -nearest-neighbor averaging. The curse of dimensionality q To capture 1% of data to form a local average, we must cover 63% of the range of each input variable. n q The expected edge length = All sample points are close to an edge of the sample. n Median distance from the origin to the closest data point: 22

2. 5 Local Methods in High Dimensions n Example 1 -NN vs. Linear q 1 -NN Sq. Bias Variance n q As p increases, MSE & bias tends to 1. 0. Linear model n = 0. increases linearly as a Expecting on x 0, the expected EPE function of p. By relying on rigid assumptions, the linear model has no bias at all and negligible variance, while the error in 1 -nearest neighbor is larger. 23

2. 6 Statistical Models, Supervised Learning and Function Approximation n Finding a useful approximation to function that underlies the predictive relationship between the inputs and outputs. q q Supervised learning: machine learning point of view Function approximation: mathematics and statistics point of view 24

2. 7 Structured Regression Models n Nearest-neighbor and other local methods face problems in high dimensions. q q n They may be inappropriate even in low dimensions. Need for structured approaches. Difficulty of the problem q q q Infinitely many solutions to minimizing RSS. Unique solution comes from restrictions on f. 25

2. 8 Classes of Restricted Estimators n Methods categorized by the nature of the restrictions. q Roughness penalty and Bayesian methods n q Kernel methods and local regression n n q Penalizing functions that too rapidly vary over small regions of input space. Explicitly specifying the nature of local neighborhood (kernel function). Need adaptation in high dimensions. Basis functions and dictionary methods n Linear expansion of basis functions. 26

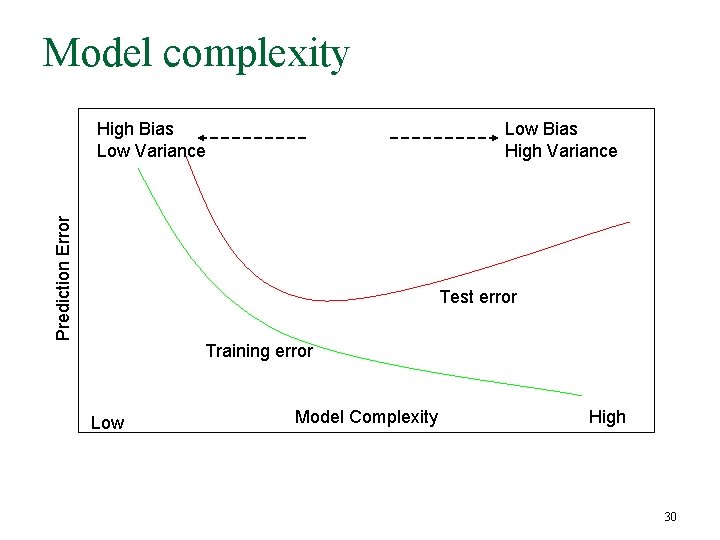
2. 9 Model Selection and the Bias. Variance Tradeoff n All models have a smoothing or complexity parameter to be determined q q q Multiplier of the penalty term Width of the kernel Number of basis functions 27

Bias-Variance tradeoff Essential with ε, no way to reduce To reduce one might increase the other. Tradeoff! 28

Bias-Variance tradeoff in k. NN 29

Model complexity Low Bias High Variance Prediction Error High Bias Low Variance Test error Training error Low Model Complexity High 30