Chapter 1 Inductive and Deductive Reasoning MAIN ISSUES

Chapter 1 Inductive and Deductive Reasoning

MAIN ISSUES Ø The pre-requisites for this chapter have not been since grade 7 (factoring, line constructions, . . ); Need to spend time reviewing before beginning the chapter Ø Some practice problems in the text have not been introduced with examples; accommodated this by providing the class with examples (do as a class) and additional practice problems (individual/group work)

MISCONCEPTIONS Ø Some students have difficulty differentiating between inductive and deductive reasoning, and when to use which one; a summary sheet attached in the notes will help to clear these misunderstandings. Ø Analyzing puzzles is another problem students have a tough time understanding; having a separate assignment where students could first create their own puzzle and give their reasoning behind choices made.

MISCONCEPTIONS Ø Recognizing what kind of pattern exists can sometimes take a while; students will get better as they practice and attempt to create and decipher various patterns – remind students to take the time to think about what comes next…

OPTICAL ILLUSIONS

INDUCTIVE VS DEDUCTIVE REASONING

Chapter 2: Properties of Angles and Triangles

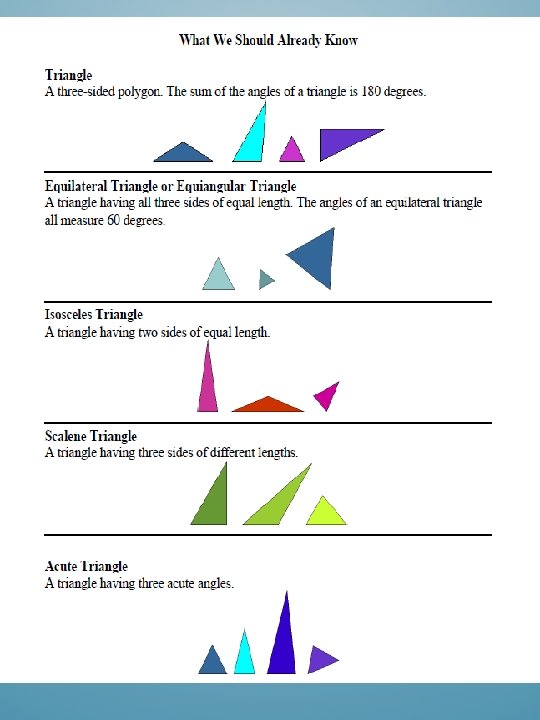
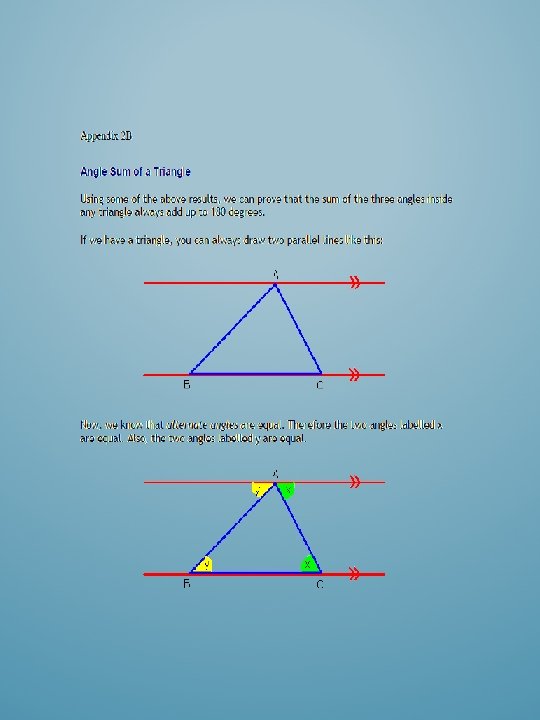
Issues Since Geometry isn’t covered in Math 10 C and some prerequisites go back to Grade 6, more review should have been incorporated. 2. 2: No example showing students how to recognize and correct errors in a proof. 2. 3: Students aren’t shown proof as to why angles of a triangle have a sum of 180 o

Resources ØInteractive review: http: //www. mathwarehouse. com/ geometry/triangles/. ØTriangles: http: //www. mathleague. com/help/ geometry/polygons. htm ØRevision http: //www. mathsrevision. net/gcs e/pages. php? page=17

Chapter 3: Acute Triangle Trigonometry

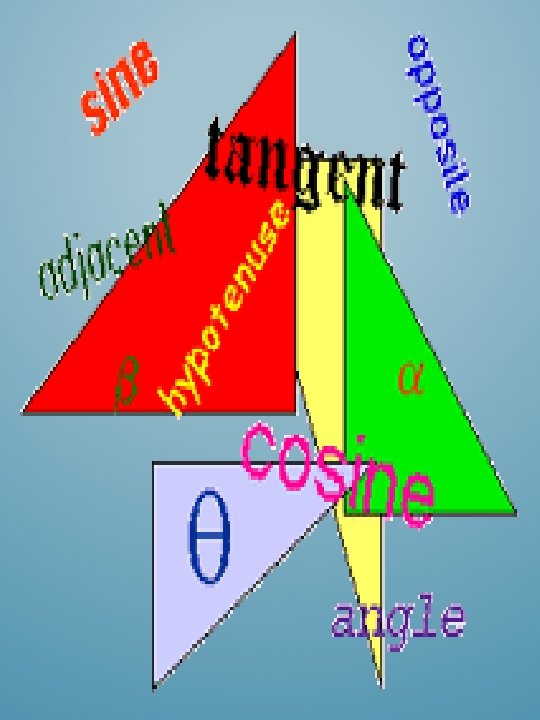
Issues Ø 3. 1: No guidance into trigonometry. Students are only given problems. Some example questions would be beneficial. ØLess differentiation included in proofs and examples. ØStudents are not taught how to use their calculator to compute cosine or sine equations.

Misconceptions ØStudents don`t know when to use the sine law, cosine law, or trigonometric ratios. ØSome students may still try to use the Pythagorean Theorem

Chapter 4: Radicals

Issues ØSome of the achievement indicators are also prerequisites and aren`t covered in this chapter but the students still have problems to complete using these concepts. For example, Section 4. 1 and indicator 3. 1 Ø 4. 5: Again, there is no example showing the students how to solve the problem. Since students have done this the previous year, a simple pedagogical technique may help. Ø 4. 6: AI 4. 1: This achievement indicator should be changed to section 4. 4 instead. In 4. 4, each step is discussed and there is more emphasis on the indicator. (determining restrictions on the variable. )

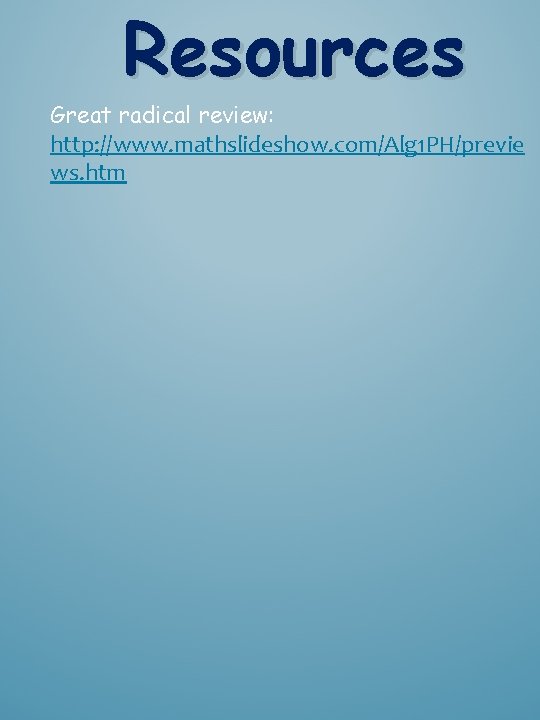
Resources Great radical review: http: //www. mathslideshow. com/Alg 1 PH/previe ws. htm

Misconseptions ØStudents get stuck when asked to simplify radical expressions involving variables in the radicands ØStudents get intimidated easily with radical expressions. Start with straight forward examples and work ease your way in.

CHAPTER 5 STATISTICAL REASONING

ISSUES Ø Students haven’t seen Measures of Central Tendency since grade 7; it is an essential part of statistical reasoning Ø Students may rely on the calculator to calculate their standard deviation and mean values; students need to be able to complete it both ways Ø The textbook does not provide proper instructions for how to use the graphing calculator to display the mean and standard deviation of a given data (Attached supplementary resources)

REVIEW OF PRIOR SKILLS:

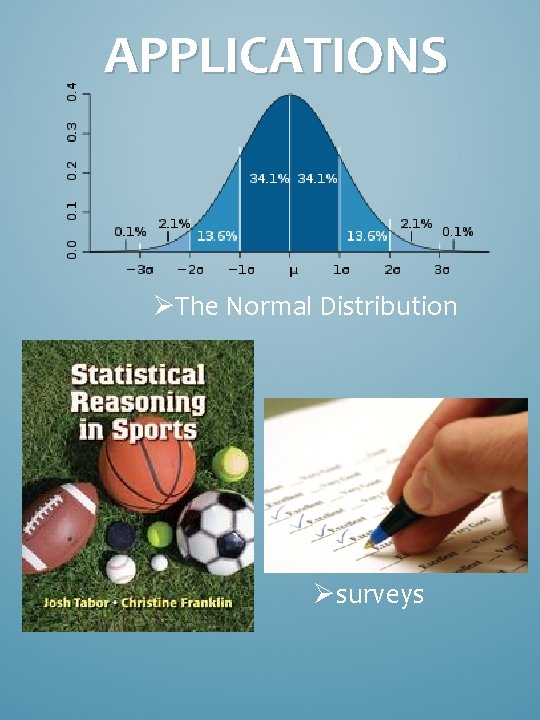
APPLICATIONS ØThe Normal Distribution Øsurveys

USING TECHNOLOGY Ø ICT outcomes: Ø Students use technology to investigate and or/solve problems Ø Students will use electronic research techniques to construct personal knowledge and meaning Ø Students will access, use and communicate information from a variety of technologies Ø Students will seek alternative viewpoints, using information technologies

MISCONCEPTIONS Ø Even though statistics goes hand-in-hand with numbers, it is actually based on inductive reasoning. This means students will need to recall what they learned from chapter one (Go over ‘reasoning summary’ worksheet) Ø Even with the technology present, students need to make sure they can compute the mean and standard deviations on paper, or mentally. It will enhance their mental mathematics skills – even though this is not one of the properties listed it increases mathematical understanding if students continually practice ‘mental math’.

ICT Outcomes C 6 -4. 1: Ø Students will use technology to investigate and/or solve problems. Ø Investigate and solve problems of prediction, calculation and inference. C 6 -4. 3: Ø Students will use technology to investigate and/or solve problems. Ø Manipulate data by using charting and graphing technologies in order to test inferences and probabilities.

MAIN ISSUES Main Issues Section 6. 1: The curriculum says that graphing occurs. The textbook actually covers some review of quadratic characteristics, but graphing is not included until later sections. Ø Nature of Mathematics: Mental mathematics is not included in the Program of Studies. However, the text does implicitly teach it by asking students to describe and visualize in questions throughout the chapter.

STUDENT MISCONCEPTIONS Ø In problem solving, students have difficulties relating quantities to the variables in the function. Ø Students may become dependent on their calculator to ‘find the answer’ for them. (They will look for the maximum in a table of values on the calculator instead of finding it by hand).

Valuable Websites to check Out http: //people. hofstra. edu/steve n_r_costenoble/Graf. html http: //www. purplemath. com/mod ules/grphquad. htm

CHAPTER 7: QUADRATIC EQUATIONS

ICT OUTCOMES C 6 -4. 1: Ø Students will use technology to investigate and/or solve problems. Ø Investigate and solve problems of prediction, calculation and inference. C 6 -4. 3: Ø Students will use technology to investigate and/or solve problems. Ø Manipulate data by using charting and graphing technologies in order to test inferences and probabilities.

If you can solve this, thank a math teacher!

MAIN ISSUES ØNature of Mathematics: Mental mathematics is not included in the Program of Studies. However, the text does implicitly teach it by asking students to describe and visualize in questions throughout the chapter. ØThis chapter should be easier than the previous, since the quadratic formula involves ‘plug and play’ questions which students like. However, they make small mistakes by not being careful.

STUDENT MISCONCEPTIONS ØIt is sometimes difficult for students to keep track of the variables, so a solution may be to make sure they write out all their steps (I. e. a=1, b=2, c=3)

STUDENT MISCONCEPTIONS ØThere may be inadmissible solutions as possible answers. Students tend to forget they must verify all solutions. Ø They also need to be aware that in problem solving, an inadmissible solution will not be logical. Number sense means knowing when an answer makes sense and when it does not.

CHAPTER 8 PROPORTIONAL REASONING what is the proportional relationship between Mr. Short and Mr. Tall?

MISCONCEPTIONS ØStudents need to understand that the proportional relationship is not always the same across each problem presented. ØThe unit given in scale factors has an impact on the actual size of the object.

SUPPLEMENTS

NATURE OF MATHEMATICS Ø Change, constancy, patters, and relations are all essential components to this chapter. Ø Spatial sense is also addressed as students work with scale factors and its effects on the area, perimeter, surface area and volume of 2 -D and 3 -D objects.

MATHEMATICAL PROCESSES Ø Students use almost all the mathematical processes in proportional reasoning; being able to make connections and communicate those connections will help students to build their problem solving skills. Ø It also makes it easier to visualize the problem as they attempt to solve it

Practice problems involving ratios: