Chapter 1 Getting Started Understanding Basic Statistics Fifth

Chapter 1 Getting Started Understanding Basic Statistics Fifth Edition By Brase and Brase Prepared by Jon Booze

What is Statistics? • Many definitions could apply. A few ideas about the subject: - “The science of studying variation. ” - “Description of and inference from data. ” - The art of making decisions from data in the face of error. ” What should be clear is that it’s all about data, analysis, and explaining and understanding variation. © Cengage Learning. All rights reserved. 1 | 2

What is Statistics? • • Collecting data Organizing data Analyzing data Interpreting data • Statistician’s Creed: “In God we trust…. all others, bring data!” © Cengage Learning. All rights reserved. 1 | 3

Individuals and Variables • Individuals are people or objects included in the study. (Also known as the “experimental units” or “subjects. ”) • Variables are characteristics of the individual to be measured or observed. They change from individual to individual…or over time. ) © Cengage Learning. All rights reserved. 1 | 4

Variables • Qualitative Variable – The variable describes an individual through grouping or categorization. (e. g. hair color, religion, college major, birth city, etc. ) • Quantitative Variable – The variable is numerical, so operations such as adding and averaging make sense. (e. g. weight, height, temperature of liquid, length of time, etc. ) © Cengage Learning. All rights reserved. 1 | 5

Data • Population Data – The data are from every individual of interest. • Sample Data – The data are from only some of the individuals of interest. That is, a sample is a subset of our population. © Cengage Learning. All rights reserved. 1 | 6
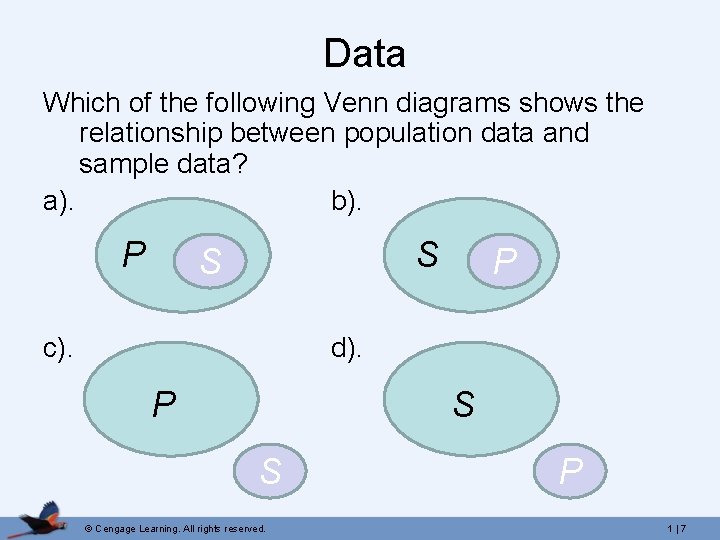
Data Which of the following Venn diagrams shows the relationship between population data and sample data? a). b). P S S c). P d). P S S © Cengage Learning. All rights reserved. P 1 | 7

Two VERY Important Terms • Parameter – is a numerical measure that describes an aspect of a population • Statistic – is a function of data from a sample. • Remember the Mnemonic Device…. “P”: PARAMETER corresponds to POPULATION “S”: STATISTIC corresponds to SAMPLE © Cengage Learning. All rights reserved. 1 | 8

Two VERY Important Terms Just a quick note: With one exception that we will get later, we typically represent: • PARAMETERS – using lowercase Greek characters (e. g. μ, σ, ρ, etc. ) • STATISTICS – using standard Arabic characters (e. g. s, s 2, r, etc. ) © Cengage Learning. All rights reserved. 1 | 9

Levels of Measurement • Nominal Level – The data consists of names, labels, or categories. • Ordinal Level – The data can be ordered, but the differences between data values are meaningless. © Cengage Learning. All rights reserved. 1 | 10

Levels of Measurement • Interval Level – The data can be ordered and the differences between data values are meaningful. • Ratio Level – The data can be ordered, differences and ratios are meaningful, and there is a meaningful zero value. NOIR: Nominal Ordinal Interval Ratio © Cengage Learning. All rights reserved. 1 | 11

Levels of Measurement Classify on our “NOIR” scale: 1. Age of a person. 2. Distance travelled from home to work. 3. Grades recorded on an A, B, C, D, F scale. 4. Undergraduate majors’ fields of study at EUP. 5. Temperature of a liquid in degrees Fahrenheit. 6. Religious Affiliation of voters. 7. Rating of oral presentations on a 1, 2, 3, . . . , 9 scale. 8. Number of children in a family. © Cengage Learning. All rights reserved. 1 | 12

Levels of Measurement Classify on our “NOIR” scale: 9. Response to a question on a Likert Scale (Strongly Disagree, Neutral, Agree, Strongly Agree). 10. Whether a person in a study is in the control group or the experimental group. © Cengage Learning. All rights reserved. 1 | 13

Levels of Measurement Solutions: 1. 2. 3. 4. 5. 6. 7. Ratio Ordinal Nominal Interval Nominal Ordinal © Cengage Learning. All rights reserved. 8. Ratio 9. Ordinal 10. Nominal 1 | 14

Two Approaches to Statistics • Descriptive Statistics: Organizing, summarizing, and graphing information from samples. • Inferential Statistics: Using information from a sample to draw conclusions about a population. © Cengage Learning. All rights reserved. 1 | 15
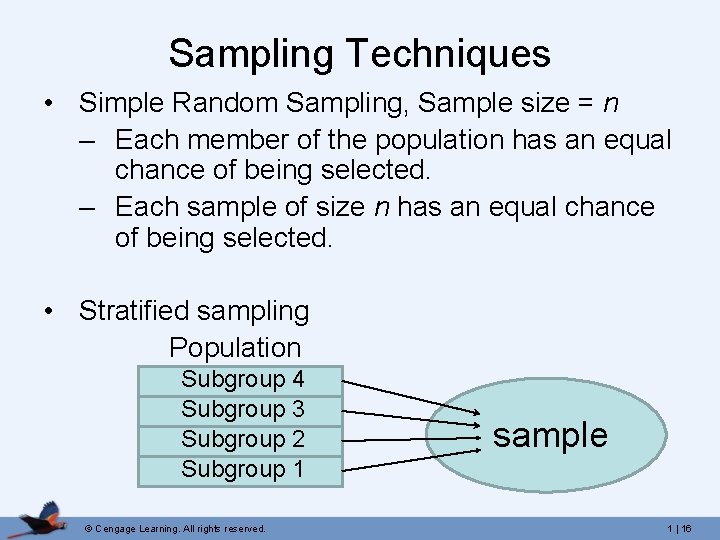
Sampling Techniques • Simple Random Sampling, Sample size = n – Each member of the population has an equal chance of being selected. – Each sample of size n has an equal chance of being selected. • Stratified sampling Population Subgroup 4 Subgroup 3 Subgroup 2 Subgroup 1 © Cengage Learning. All rights reserved. sample 1 | 16

Sampling Techniques • Cluster sampling – Population is naturally divided into preexisting segments. – Make a random selection of clusters, then select all members of each cluster. • Systematic sampling – Number every member of the population. – Select every kth member. • Convenience sampling - Collect sample data from a readily-available population database. © Cengage Learning. All rights reserved. 1 | 17

Sampling Techniques Which of the five sampling designs is being employed? (Simple Random, Stratified, Cluster, Systematic, or Convenience? ) 1. A politician wants to survey his constituents. To do so, he polls 100 democrats in his district, 125 republicans, and 20 independents. 2. Wal-Mart would like to perform demographic analysis of its shoppers. So starting at 8: 00 am, the Wal-Mart greeter is asked to survey every 20 th customer who enters the store. © Cengage Learning. All rights reserved. 1 | 18

Sampling Techniques 3. A doctor is assessing a new treatment technique. She utilizes this treatment on all asthma patients she sees for a one month period. 4. A company wishes to survey its employees. There are 800 employees, an a random number is assigned to each. Fifty employees are selected using a random number table. 5. Residence life wants to examine student interests. Of the seven dorms, three dorms are randomly selected. Every student in the dorms selected is surveyed. © Cengage Learning. All rights reserved. 1 | 19

Sampling Techniques Solutions to Sampling Technique Problems. 1. 2. 3. 4. 5. Stratified Systematic (1 -in-k) Convenience Simple Random Sample (SRS) Cluster © Cengage Learning. All rights reserved. 1 | 20

Census vs. Sample • In a census, measurements or observations are obtained from the entire population (uncommon and often impractical). • In a sample, measurements or observations are obtained from part of the population (common). © Cengage Learning. All rights reserved. 1 | 21

Observational Studies and Experiments • Observational Study – Measurements are obtained in a way that does not change the response or the variable being measured. (No treatment is applied. ) • Experiment – A treatment is applied in order to observe its effect on the variable being measured. The research controls this primary variable. © Cengage Learning. All rights reserved. 1 | 22

Experiment • Used to determine the effect of a treatment. • Experimental design needs to control for other possible causes of the effect. – Placebo effect. – Lurking variables. • To minimize these confounds, create one or more control groups that receive no treatment. © Cengage Learning. All rights reserved. 1 | 23

Experiment Designs • Randomization – A random process is used to assign individuals to a treatment group or to a control group. • Double-Blinding – minimizes the unintentional transfer of bias between researcher and subject. © Cengage Learning. All rights reserved. 1 | 24

Surveys • Collecting data from respondents by asking them questions. Survey Pitfalls • Nonresponse → undercoverage of population. • Truthfulness – respondents sometimes lie. • Faulty recall of respondent • Hidden bias – due to poor question wording. • Vague wording – “sometimes”, “often”, “seldom” • Interviewer influence – who is asking the questions and in what manner. • Voluntary response – relatively interested individuals are more likely to participate. © Cengage Learning. All rights reserved. 1 | 25
- Slides: 25