Chapter 1 Functions and Limits 1 3 Rates

Chapter 1 Functions and Limits 1. 3 Rates of Change and Tangents to Curves 1. 4

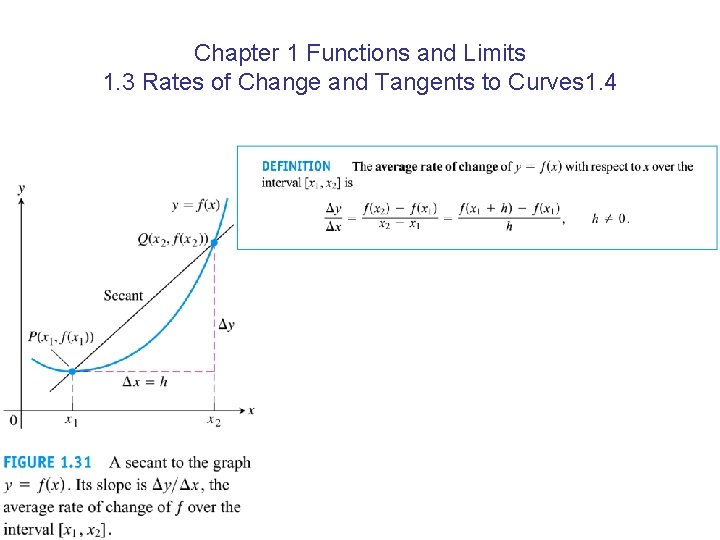
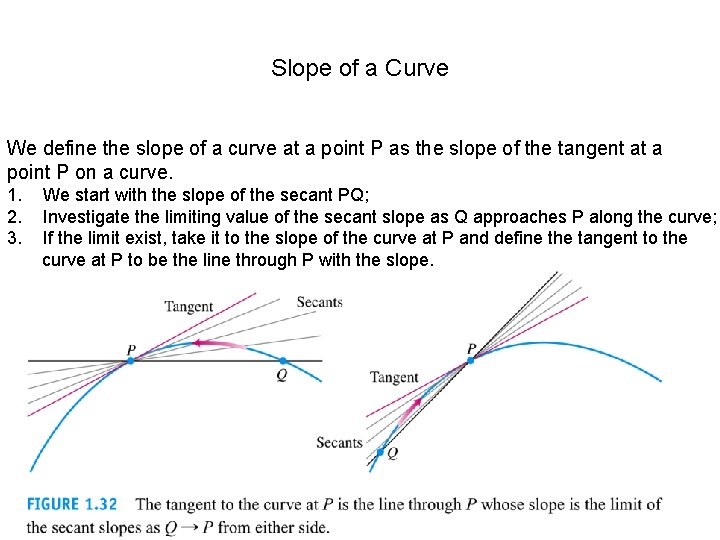
Slope of a Curve We define the slope of a curve at a point P as the slope of the tangent at a point P on a curve. 1. 2. 3. We start with the slope of the secant PQ; Investigate the limiting value of the secant slope as Q approaches P along the curve; If the limit exist, take it to the slope of the curve at P and define the tangent to the curve at P to be the line through P with the slope.

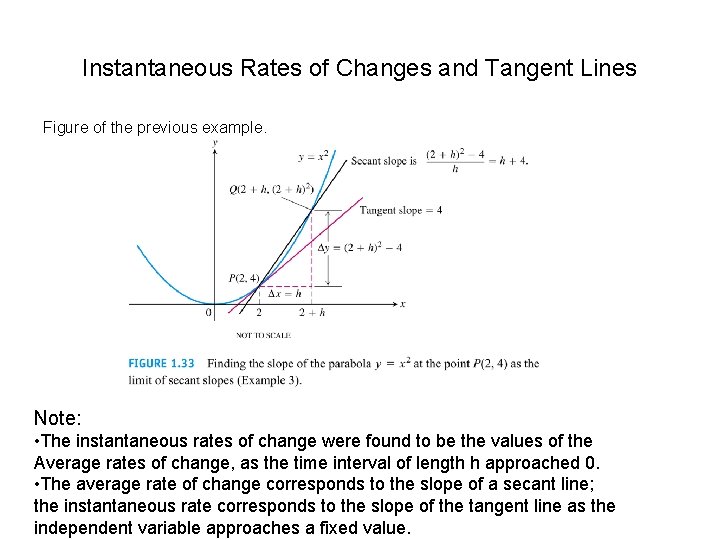
Example Find the slope of the parabola y=x 2 at the point P(2, 4). Write an equation for the tangent to the parabola at this point. Solution:

Instantaneous Rates of Changes and Tangent Lines Figure of the previous example. Note: • The instantaneous rates of change were found to be the values of the Average rates of change, as the time interval of length h approached 0. • The average rate of change corresponds to the slope of a secant line; the instantaneous rate corresponds to the slope of the tangent line as the independent variable approaches a fixed value.

1. 4 Limit of a Function and Limit Laws Many ideas of calculus originated with the following two geometric problems:

Traditionally, that portion of calculus arising from the tangent line problem is called differential calculus and that arising from the area problem is called integral calculus • Tangent lines and limits • Areas and limits • Decimals and limits*

Limits The most basic use of limits is to describe how a function behaves as the independent variable approaches a given value. For example, let us examine the behavior of the function for x values closer and closer to 2. We can see that the values of f(x) get closer and closer to 3 as values of x are selected closer and closer to 2 on either side of 2.

Limits We describe this by saying that the “limit of approaches 2 from either side”, and we write is 3 as x

Limits (An Informal View) Note: Since x is different from a, the value of f at a or even whether f is defined at a, has not bearing on the limit L

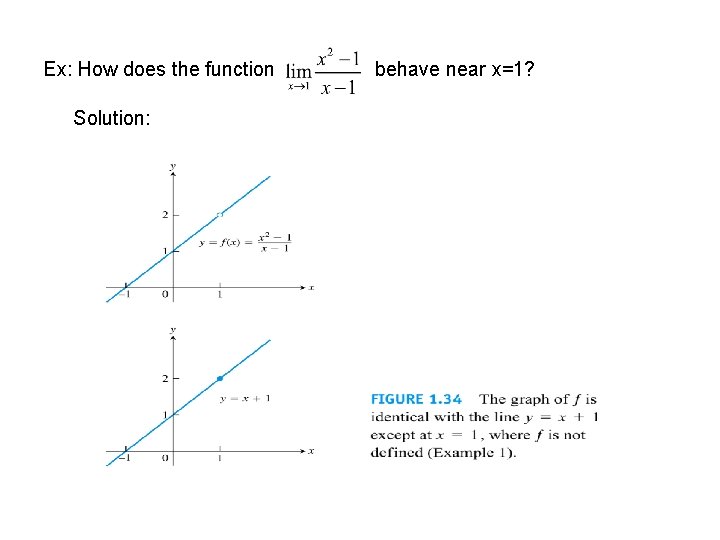
Ex: How does the function Solution: behave near x=1?

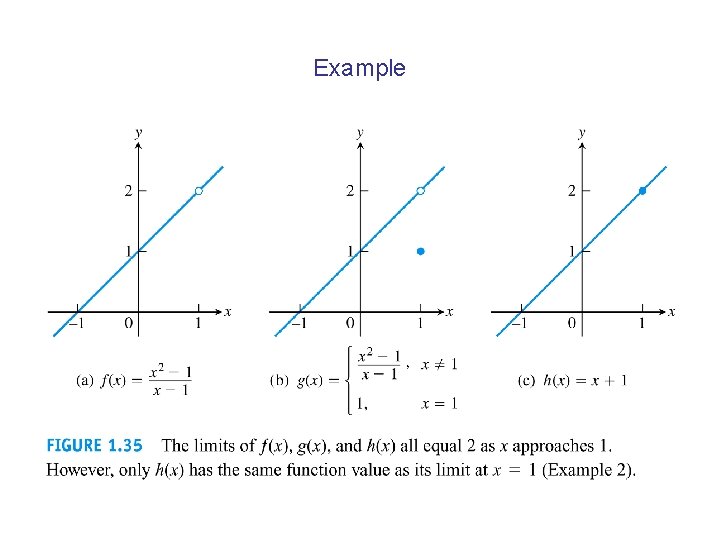
Example

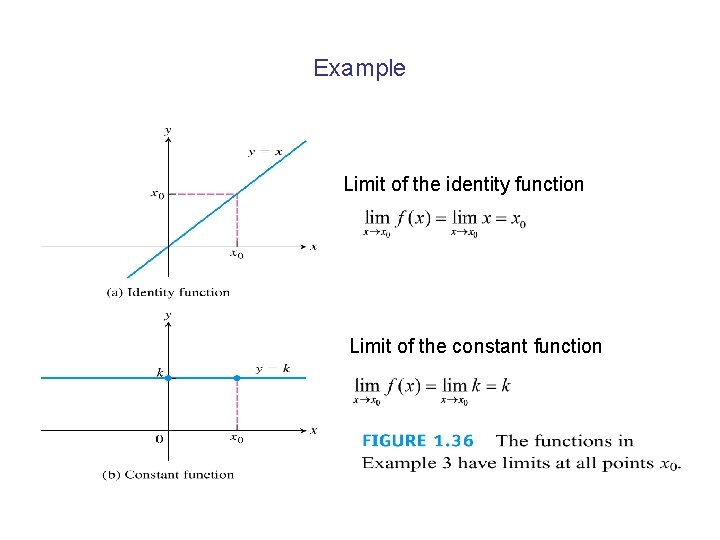
Example Limit of the identity function Limit of the constant function

Example Discuss the behavior of the following functions as x 0.

The Limit Laws

Examples Solution:

Example, Solution: Example: Solution:

Theorems

Examples For example, Solution: Example, Solution:

Eliminating Zero Denominators Algebraically When p(x)/q(x) is a rational function for which p (a) =0 and q(a)=0, the numerator and denominator must have one or more common factors of x – a. In this case, the limit of p(x)/q(x) as x a can be found by canceling all common factors of x – a first. Here are some examples…

For example, Find Solution:

Example: Find Solution:

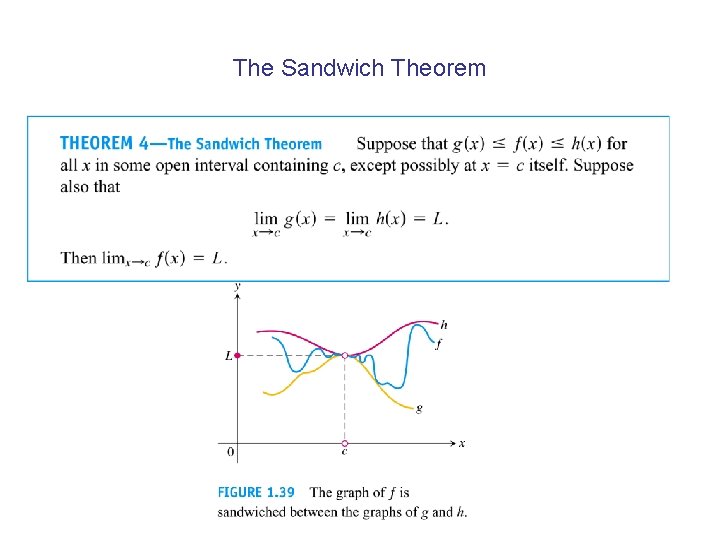
The Sandwich Theorem

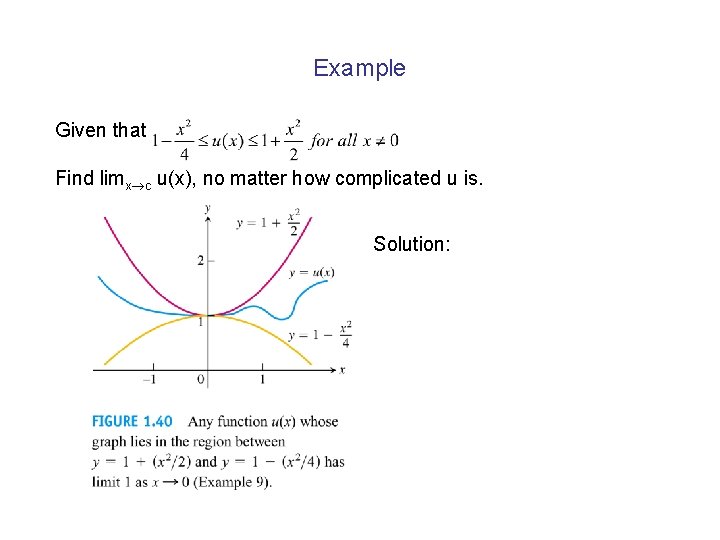
Example Given that Find limx c u(x), no matter how complicated u is. Solution:

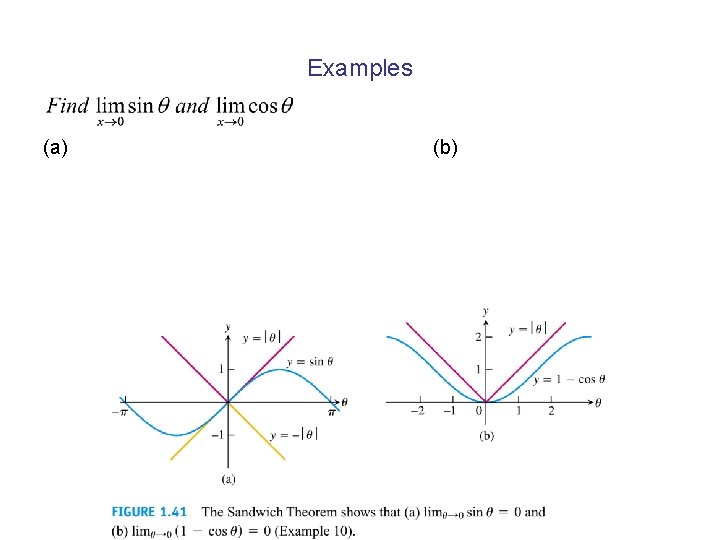
Examples (a) (b)

Theorem

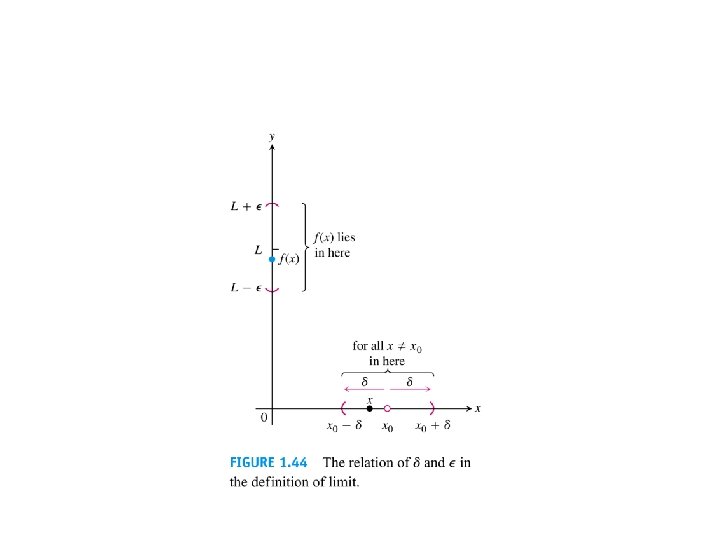
1. 5 The Precise Definition of a Limit

Examples: Testing the Definition

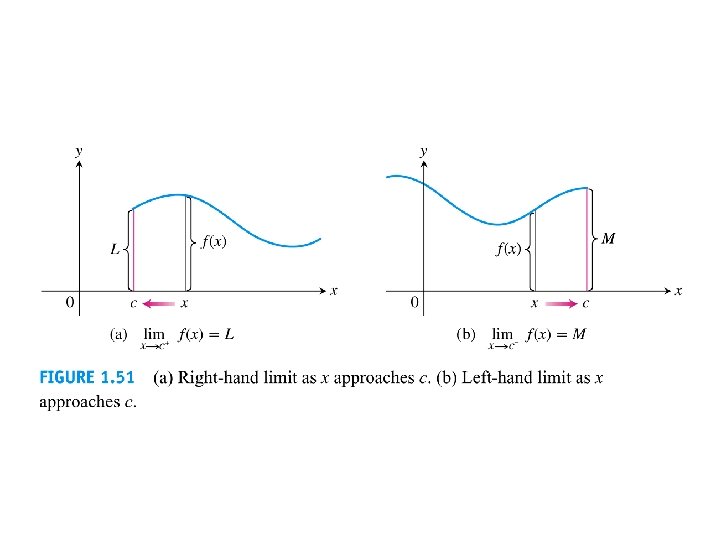
1. 6 One-sided Limits For example: consider the function

As x approaches 0 from the right, f(x) approaches 1, and similarly, as x approaches 0 from the left, f(x) approaches -1. We denote this by Here “+” indicates a limit from the right and “-” indicates a limit from the left.

One-Sided Limits

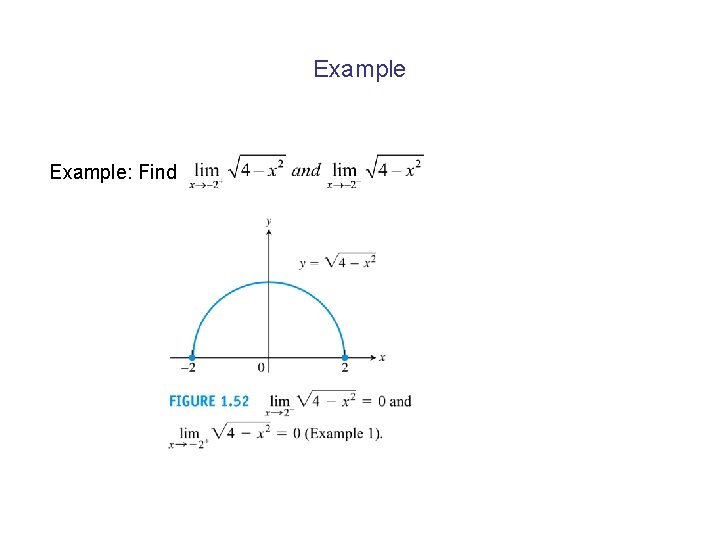
Example: Find

The relation between one-sided limits and two-sided limits In general, there is no guarantee that a function f will have a two-sided limit at a given point. In this case, we say that does not exist. Similarly for one-sided limits. Here we state the relation without formal proof

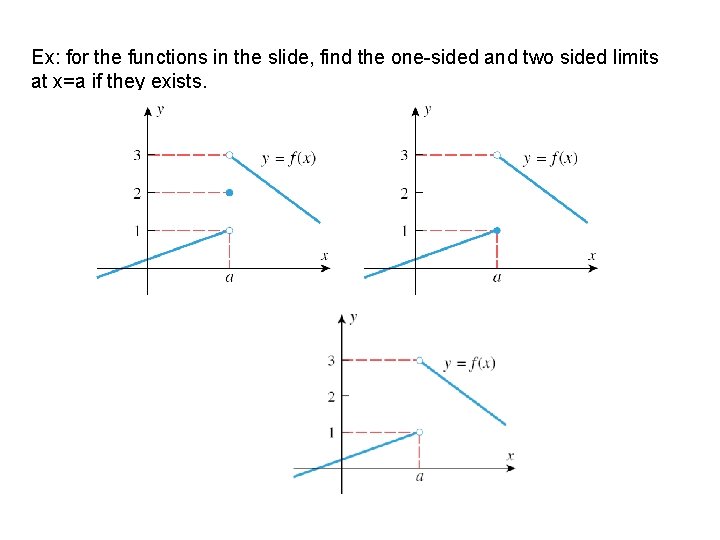
Ex: for the functions in the slide, find the one-sided and two sided limits at x=a if they exists.

Solution:

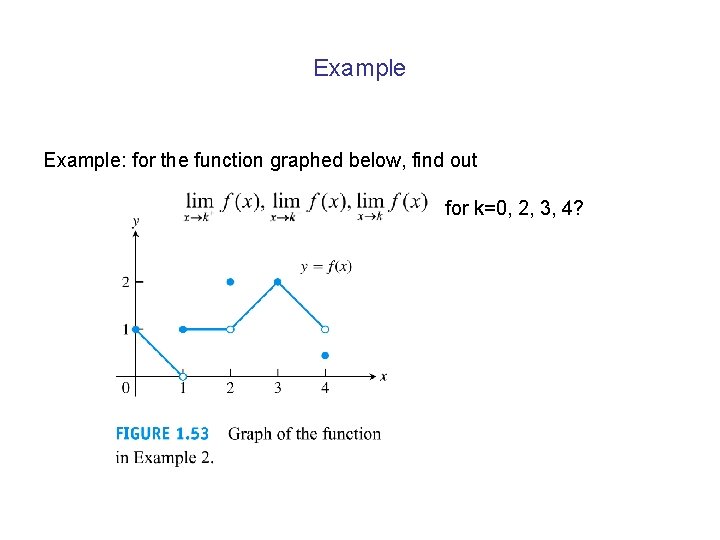
Example: for the function graphed below, find out for k=0, 2, 3, 4?

Limits Involving (sin / ) A central fact about sin / is that in radian measure its limit as 0 is 1. We can see this from the figure below, and confirm it algebraically using the Sandwich Theorem.

Examples Find the following limits.

Example:

Example:

1. 7 CONTINUITY Intuitively, the graph of a function can be described as a “continuous curve” if it has not breaks or holes. The graph of a function has a break or hole if any of the following conditions occur: • The function f is undefined at c • The limit of f(x) does not exist as x approaches c • The value of the function and the value of the limit at c are different.

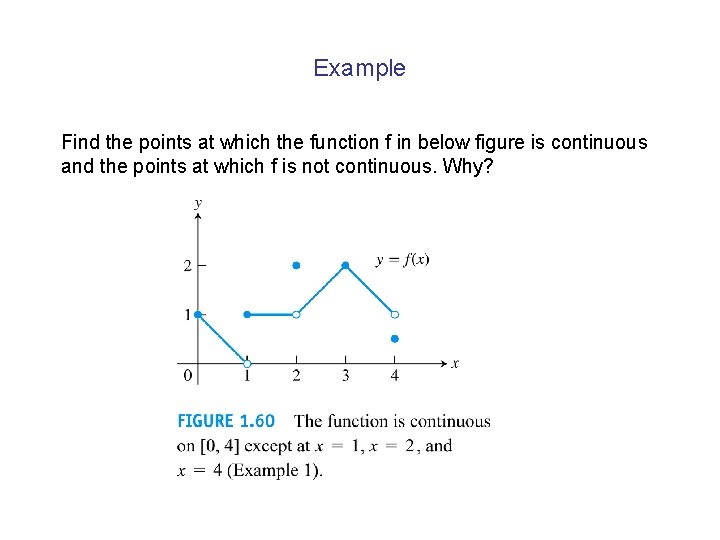
Example Find the points at which the function f in below figure is continuous and the points at which f is not continuous. Why?

Continuity at a Point If a function is defined on an open interval containing c, except possibly at c itself, and f is not continuous at c, then we say that f is discontinuous at c.

Definitions A function f is right-continuous (continuous from the right) at a point x=2 in its domain if A function f is left-continuous (continuous from the left) at a point x=2 in its domain if

Continuity Test For one-sided continuity and continuity at an endpoint, the limits in part 2 And part 3 of the test should be replaced by the appropriate one-sided limits.

Example: Determine whether the following functions are continuous at x=-3. Solution:

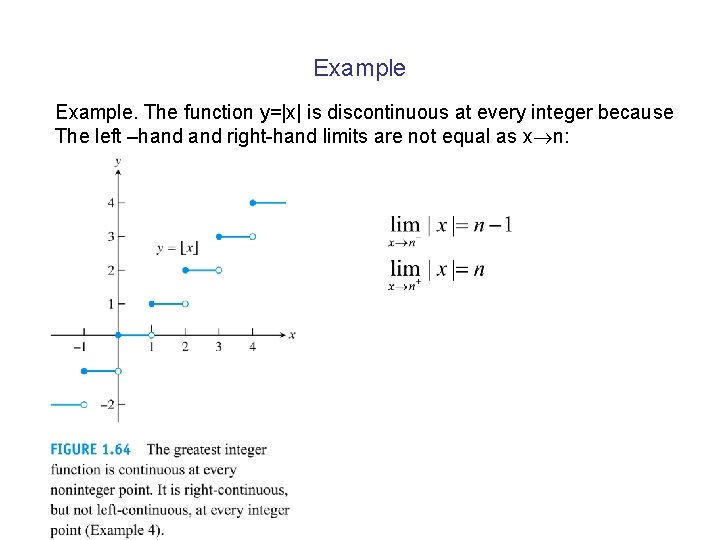
Example. The function y=|x| is discontinuous at every integer because The left –hand right-hand limits are not equal as x n:

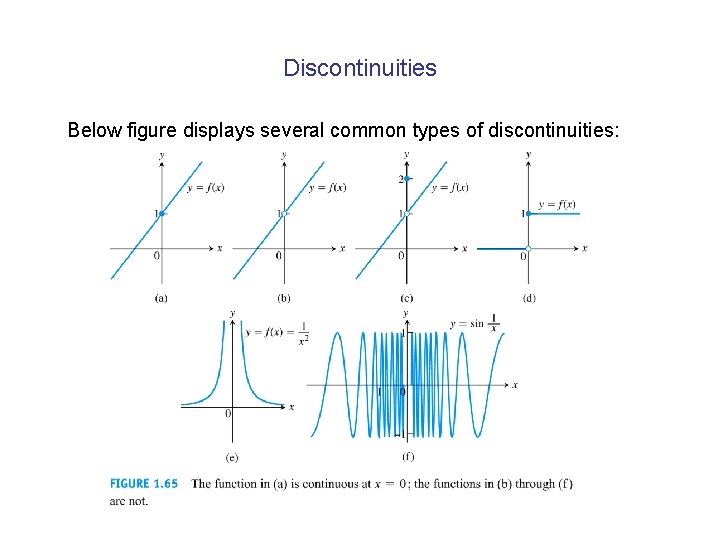
Discontinuities Below figure displays several common types of discontinuities:

Continuous Functions A function is continuous on an interval if and only if it is continuous at every point of the interval. A continuous function is one that is continuous at every point of its domain. Example: (a) the function y=1/x is continuous function. (b )the function y=x and the constant functions are continuous everywhere.

Properties of Continuous Functions Algebraic combinations of continuous functions are continuous wherever they are defined.

Examples (a) Every polynomial is continuous everywhere. (b) A rational function is continuous at every point where the denominator is nonzero, and has discontinuities at the points where the denominator is zero. (c) The functions y=sinx and y=cosx are, in fact, continuous everywhere. It follows that all six trigonometric functions are then continuous wherever they are defined.

Composites All composites of continuous functions are continuous.

Limits of Continuous Functions Generally,

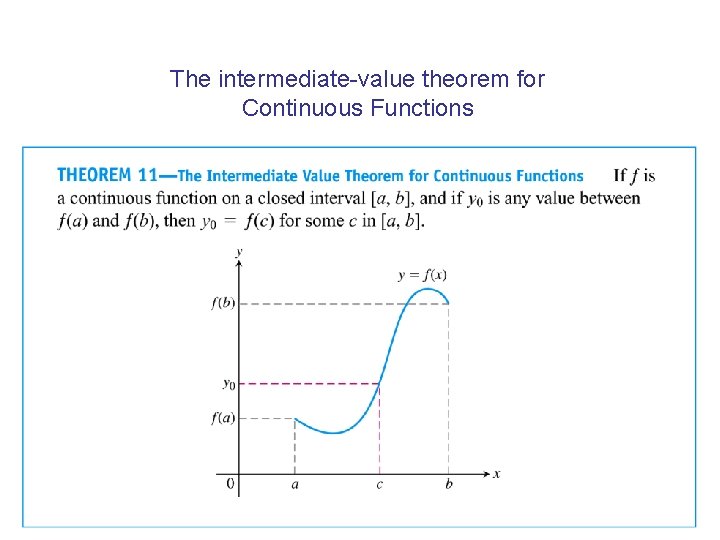
The intermediate-value theorem for Continuous Functions

Remarks for the Intermediate Value Theorem • The continuity of f on the interval is essential to the intermediate value theorem. • It implies that graph of a function continuous on an interval will be connected. • It tells that if f is continuous, then any interval on which f changes sign contains a zero of the function. (zero: solution of f(x)=0).

Approximating roots using the intermediate-value theorem Theorem. If f is continuous on [a, b], and if f(a) and f(b) are nonzero and have opposite signs, then there is at least one solution of the equation f(x)=0 in the interval (a, b).

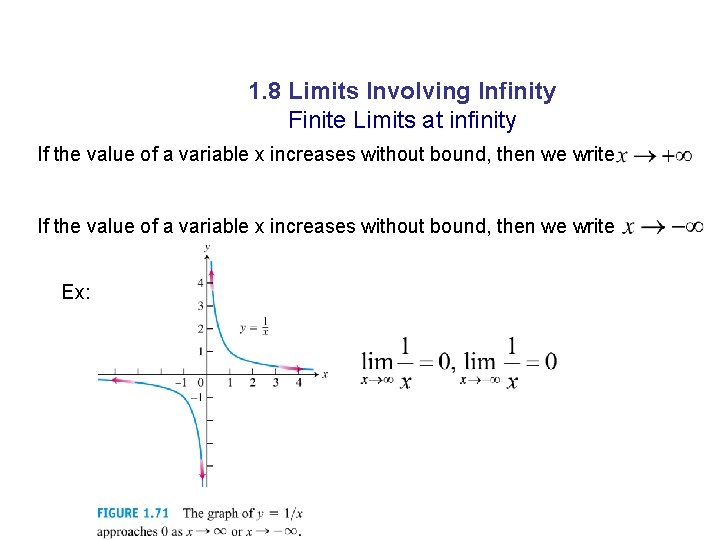
1. 8 Limits Involving Infinity Finite Limits at infinity If the value of a variable x increases without bound, then we write Ex:

Example (a) Find the limit: (b) Find the limit:

Limits at Infinity of Rational Functions Technique: divide each term in the numerator and denominator by the highest power of x that occurs in the denominator. Find

A Quick Method… The end behavior of a rational function matches the end behavior of the quotient of the highest degree term in the numerator divided by the highest degree term in the denominator. Find

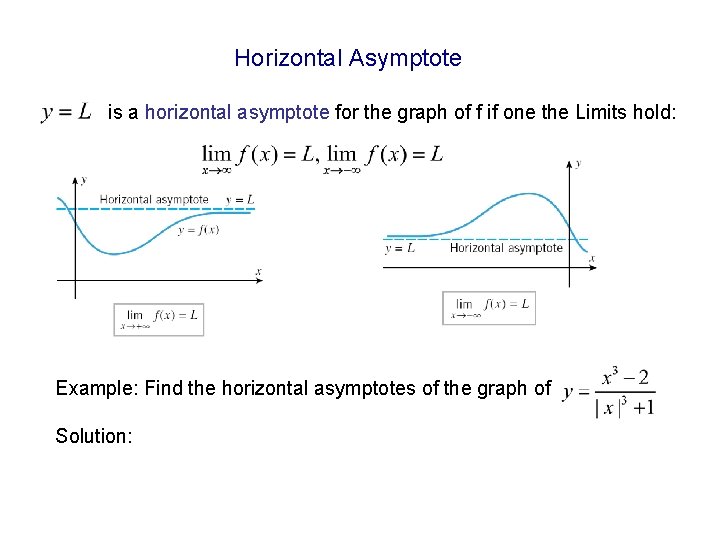
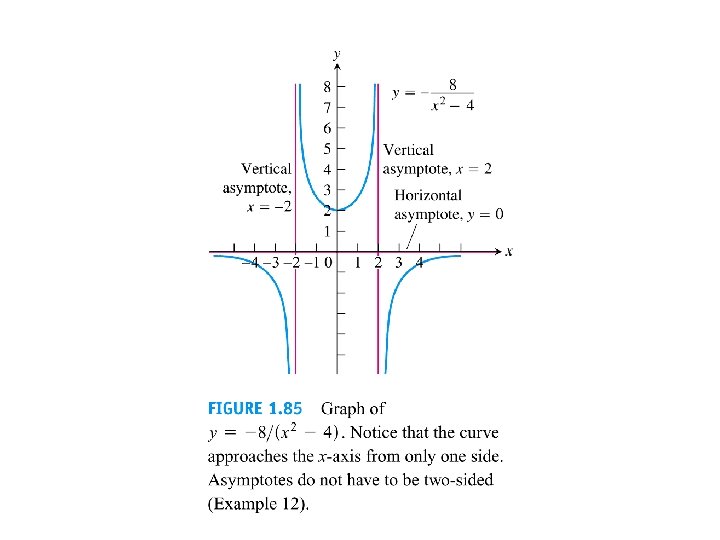
Horizontal Asymptote is a horizontal asymptote for the graph of f if one the Limits hold: Example: Find the horizontal asymptotes of the graph of Solution:

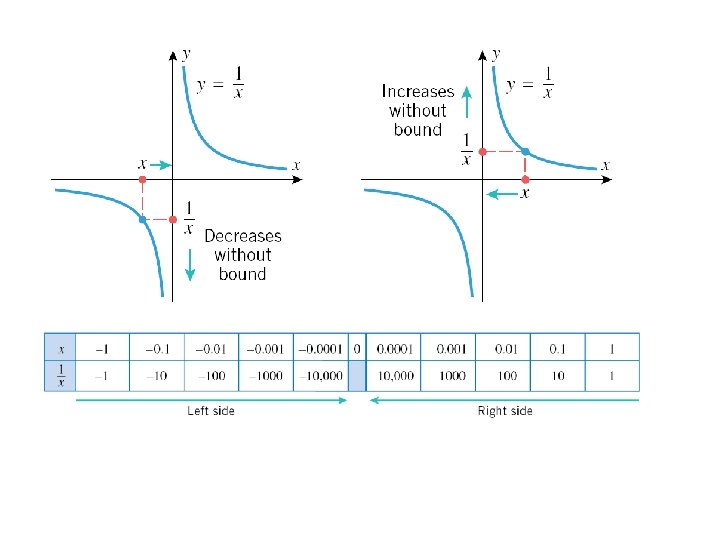
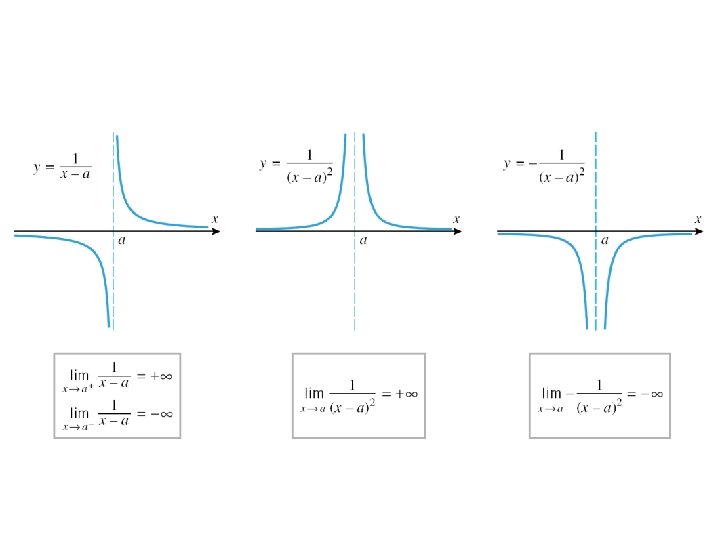
Infinite Limits Sometime one-side or two-sided limits fail to exist because the values of the function increase or decrease without bound. For example, consider We describe this behaviors by writing

Infinite Limits (An Informal View) In writing this, we are not saying that the limit exists. Nor are we saying that there is a real number , for there is no such number.

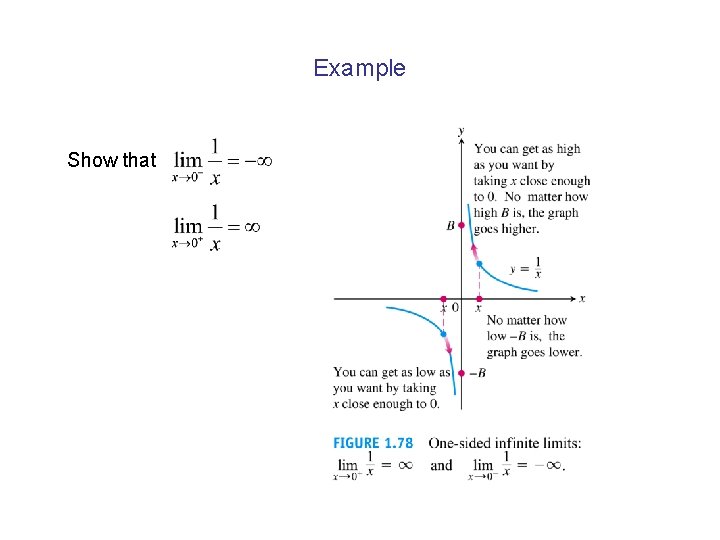
Example Show that

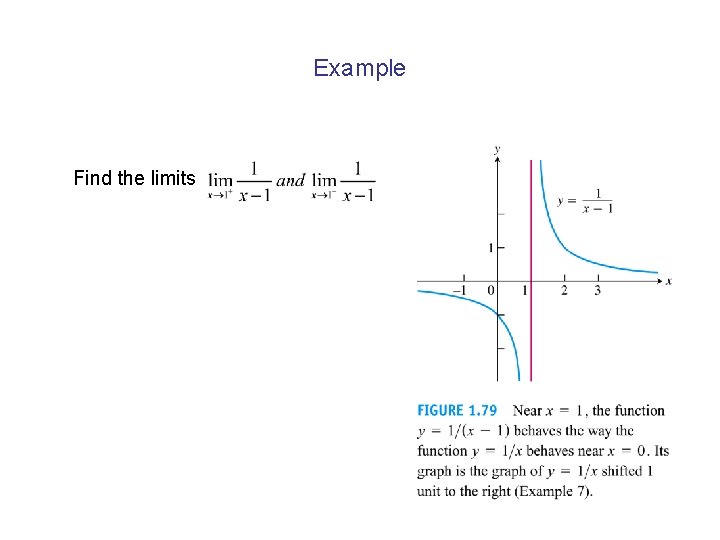
Example Find the limits

One-side limit of p (x) / q (x) when x approaches a Let p(x)/q(x) be a rational function, where the limit of the denominator is zero, and the limit of the numerator is not, then one can prove that the limit of the rational function does not exist and one of the following situations occurs: • The limit may be from one side, and from the other side.

Example Find the following limits: Solution:

Example Find Solution:

Vertical Asymptotes Example: Find the horizontal and vertical asymptotes of the graph of y=1/x.

Theorem: Let f and g be continuous on an open interval containing c. If f(c) 0, g(c)=0, and there exists an open interval containing c such that g(x) 0 for all x c in the interval, then the graph of the function given by h(x)=f(x)/g(x) has a vertical asymptote at x=c. Example: given a rational function, find the horizontal asymptotes, and Vertical asymptotes. Find the horizontal and vertical asymptotes of the graph of Solution: .