Chapter 1 FalsePosition Method of Solving a Nonlinear



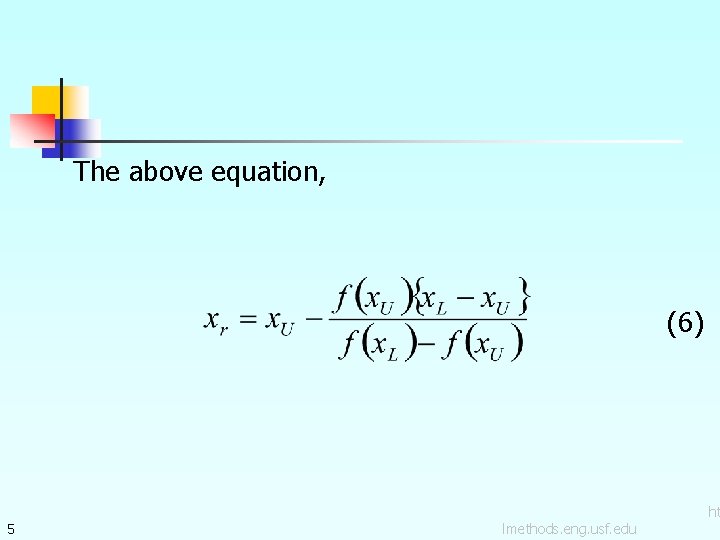














- Slides: 20

Chapter 1: False-Position Method of Solving a Nonlinear Equation http: //numericalmethods. eng. usf. edu Numerical Methods for STEM undergraduates 9/30/2020 http: //numericalmethods. eng. usf. edu 1

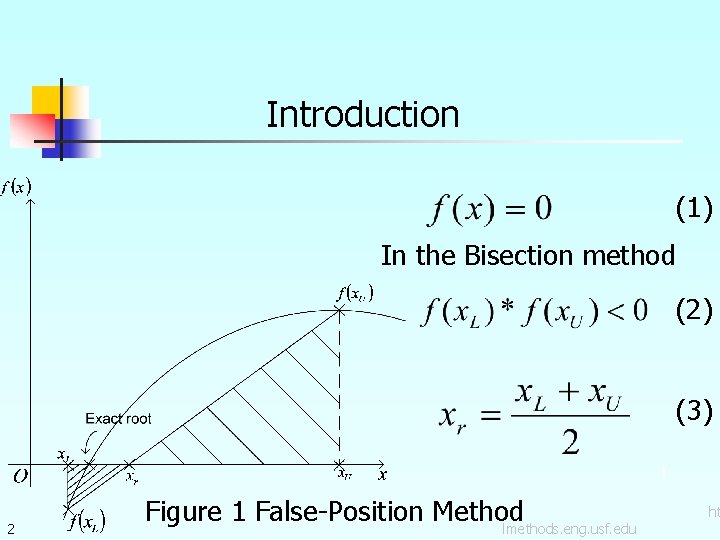
Introduction (1) In the Bisection method (2) (3) 1 2 Figure 1 False-Position Method lmethods. eng. usf. edu ht

False-Position Method Based on two similar triangles, shown in Figure 1, one gets: (4) The signs for both sides of Eq. (4) is consistent, since: 3 lmethods. eng. usf. edu ht

From Eq. (4), one obtains The above equation can be solved to obtain the next predicted root , as (5) 4 lmethods. eng. usf. edu ht
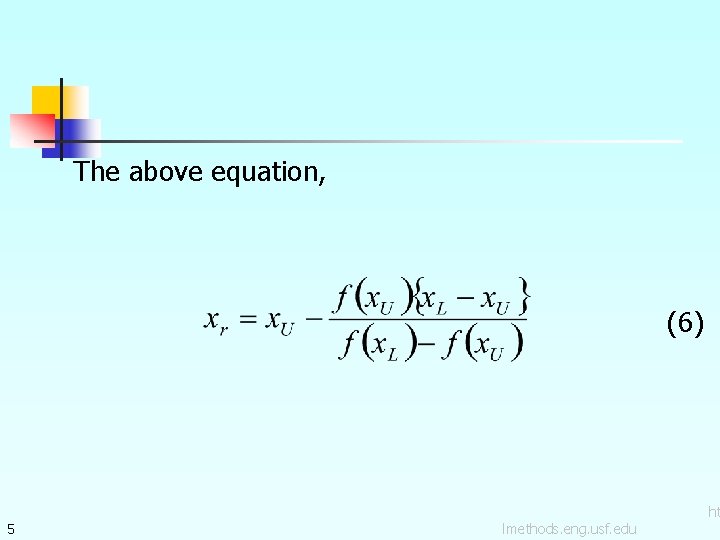
The above equation, (6) 5 lmethods. eng. usf. edu ht

Step-By-Step False-Position Algorithms 1. Choose that and as two guesses for the root such 2. Estimate the root, 3. Now check the following , then the root lies between (a) If and ; then and 6 (b) If and ; then , then the root lies between and lmethods. eng. usf. edu ht

, then the root is (c) If Stop the algorithm if this is true. 4. Find the new estimate of the root Find the absolute relative approximate error as 7 lmethods. eng. usf. edu ht

where = estimated root from present iteration = estimated root from previous iteration 5. If else stop the algorithm. , then go to step 3, Notes: The False-Position and Bisection algorithms are quite similar. The only difference is the formula used to calculate the new estimate of the root shown in steps #2 and 4! 8 lmethods. eng. usf. edu ht

Example 1 The non linear equation that gives the depth Use the false-position method of finding roots of equations. Conduct three iterations to estimate the root of the above equation. Find the absolute relative approximate error at the end of each iteration. 9 lmethods. eng. usf. edu ht

Iteration 1 10 lmethods. eng. usf. edu ht

Iteration 2 11 Hence, lmethods. eng. usf. edu ht

Iteration 3 12 lmethods. eng. usf. edu ht

Hence, 13 lmethods. eng. usf. edu ht

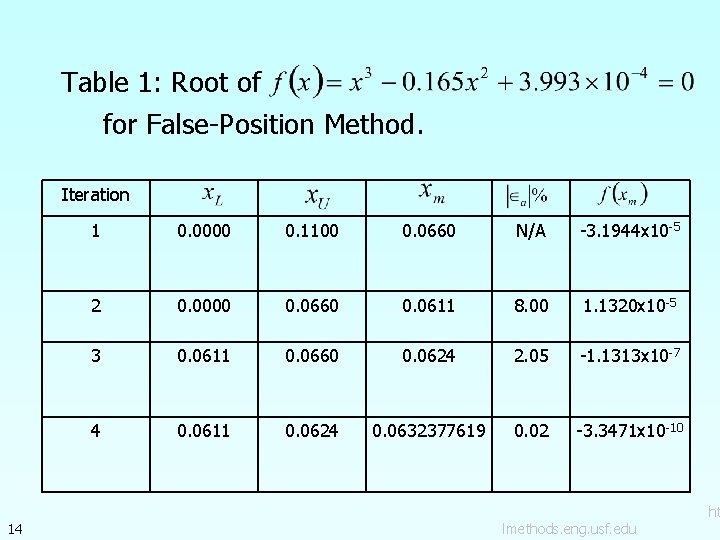
Table 1: Root of for False-Position Method. Iteration 14 1 0. 0000 0. 1100 0. 0660 N/A -3. 1944 x 10 -5 2 0. 0000 0. 0660 0. 0611 8. 00 1. 1320 x 10 -5 3 0. 0611 0. 0660 0. 0624 2. 05 -1. 1313 x 10 -7 4 0. 0611 0. 0624 0. 0632377619 0. 02 -3. 3471 x 10 -10 lmethods. eng. usf. edu ht

Exercise 1 The non linear equation that gives as Use the false-position method of finding roots of equations. Conduct three iterations to estimate the root of the above equation. Find the absolute relative approximate error at the end of each iteration. 15 lmethods. eng. usf. edu ht

Let us assume Hence, 16 lmethods. eng. usf. edu ht

Iteration 1 17 lmethods. eng. usf. edu ht

References 1. S. C. Chapra, R. P. Canale, Numerical Methods for Engineers, Fourth Edition, Mc-Graw Hill. 18 lmethods. eng. usf. edu ht

THE END http: //numericalmethods. eng. usf. edu

Acknowledgement This instructional power point brought to you by Numerical Methods for STEM undergraduate http: //numericalmethods. eng. usf. edu Committed to bringing numerical methods to the undergraduate