Chapter 1 Equations and Inequalities 1 5 Quadratic





























- Slides: 30

Chapter 1 Equations and Inequalities 1. 5 Quadratic Equations Copyright © 2014, 2010, 2007 Pearson Education, Inc. 1

Objectives: • • Solve quadratic equations by factoring. Solve quadratic equations by the square root property. Solve quadratic equations by completing the square. Solve quadratic equations using the quadratic formula. Use the discriminant to determine the number and type of solutions. Determine the most efficient method to use when solving a quadratic equation. Solve problems modeled by quadratic equations. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 2

Definition of a Quadratic Equation A quadratic equation in x is an equation that can be written in the general form where a, b, and c are real numbers, with A quadratic equation in x is also called a second-degree polynomial equation in x. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 3

The Zero-Product Principle To solve a quadratic equation by factoring, we apply the zero-product principle which states that: If the product of two algebraic expressions is zero, then at least one of the factors is equal to zero. If AB = 0, then A = 0 or B = 0. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 4

Solving a Quadratic Equation by Factoring 1. If necessary, rewrite the equation in the general form , moving all nonzero terms to one side, thereby obtaining zero on the other side. 2. Factor completely. 3. Apply the zero-product principle, setting each factor containing a variable equal to zero. 4. Solve the equations in step 3. 5. Check the solutions in the original equation. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 5

Example: Solving Quadratic Equations by Factoring Solve by factoring: Step 1 Move all nonzero terms to one side and obtain zero on the other side. Step 2 Factor Copyright © 2014, 2010, 2007 Pearson Education, Inc. 6

Example: Solving Quadratic Equations by Factoring (continued) Steps 3 and 4 Set each factor equal to zero and solve the resulting equations. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 7

Example: Solving Quadratic Equations by Factoring (continued) Step 5 Check the solutions in the original equation. Check Copyright © 2014, 2010, 2007 Pearson Education, Inc. 8

Solving Quadratic Equations by the Square Root Property Quadratic equations of the form u 2 = d, where u is an algebraic expression and d is a nonzero real number, can be solved by the Square Root Property: If u is an algebraic expression and d is a nonzero real number, then u 2 = d has exactly two solutions: or Equivalently, If u 2 = d, then Copyright © 2014, 2010, 2007 Pearson Education, Inc. 9

Example: Solving Quadratic Equations by the Square Root Property Solve by the square root property: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 10

Completing the Square If x 2 + bx is a binomial, then by adding , which is the square of half the coefficient of x, a perfect square trinomial will result. That is, Copyright © 2014, 2010, 2007 Pearson Education, Inc. 11

l l Create perfect square trinomials. x 2 + 20 x + ___ x 2 - 4 x + ___ x 2 + 5 x + ___ Copyright © 2014, 2010, 2007 Pearson Education, Inc. 12

Example: Solving a Quadratic Equation by Completing the Square Solve by completing the square: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 13

Solve by completing the square: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 14

Completing the Square Solve the following equation by completing the square: Step 1: Move quadratic term, and linear term to left side of the equation, the constant to the right side of the equation. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 15

Solving Quadratic Equations by Completing the Square Step 2: Find the term that completes the square on the left side of the equation. Add that term to both sides. The quadratic coefficient must be equal to 1 before you complete the square, so you must divide all terms by the quadratic coefficient first. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 16

Solving Quadratic Equations by Completing the Square Step 3: Factor the perfect square trinomial on the left side of the equation. Simplify the right side of the equation. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 17

Solving Quadratic Equations by Completing the Square Step 4: Take the square root of each side Copyright © 2014, 2010, 2007 Pearson Education, Inc. 18

The Quadratic Formula The solutions of a quadratic equation in general form with , are given by the quadratic formula: Copyright © 2014, 2010, 2007 Pearson Education, Inc. 19

Example: Solving a Quadratic Equation Using the Quadratic Formula Solve using the quadratic formula: a = 2, b = 2, c = – 1 Copyright © 2014, 2010, 2007 Pearson Education, Inc. 20

Example: Solving a Quadratic Equation Using the Quadratic Formula (continued) Copyright © 2014, 2010, 2007 Pearson Education, Inc. 21

The Discriminant We can find the solution for a quadratic equation of the form using the quadratic formula: The discriminant is the quantity which appears under the radical sign in the quadratic formula. The discriminant of the quadratic equation determines the number and type of solutions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 22

The Discriminant and the Kinds of Solutions to If the discriminant is positive, there will be two unequal real solutions. If the discriminant is zero, there is one real (repeated) solution. If the discriminant is negative, there are two imaginary solutions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 23

Example: Using the Discriminant Compute the discriminant, then determine the number and type of solutions: The discriminant, 81, is a positive number. There are two real solutions. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 24

Example: Application The formula models a woman’s normal systolic blood pressure, P, at age A. Use this formula to find the age, to the nearest year, of a woman whose normal systolic blood pressure is 115 mm Hg. Solution: We will solve the equation Copyright © 2014, 2010, 2007 Pearson Education, Inc. 25

Example: Application (continued) Copyright © 2014, 2010, 2007 Pearson Education, Inc. 26

Example: Application (continued) The positive solution, indicates that 26 is the approximate age of a woman whose normal systolic blood pressure is 115 mm Hg. Copyright © 2014, 2010, 2007 Pearson Education, Inc. 27

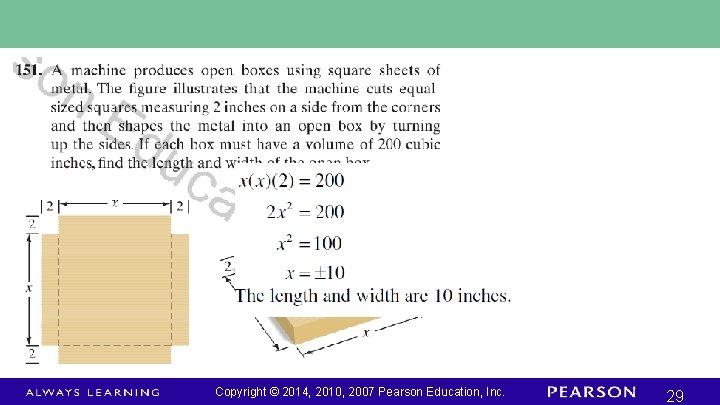
Copyright © 2014, 2010, 2007 Pearson Education, Inc. 28

Copyright © 2014, 2010, 2007 Pearson Education, Inc. 29

Copyright © 2014, 2010, 2007 Pearson Education, Inc. 30
 Chapter 6 quadratic functions and inequalities answers
Chapter 6 quadratic functions and inequalities answers Aim chapter 7
Aim chapter 7 Chapter 1 equations and inequalities
Chapter 1 equations and inequalities College algebra equations and inequalities
College algebra equations and inequalities Chapter 7 systems of equations and inequalities answers
Chapter 7 systems of equations and inequalities answers Chapter 1 expressions equations and inequalities
Chapter 1 expressions equations and inequalities Chapter 1 expressions equations and inequalities
Chapter 1 expressions equations and inequalities Chapter 1 equations and inequalities
Chapter 1 equations and inequalities Chapter 6 systems of equations and inequalities
Chapter 6 systems of equations and inequalities Chapter 9 quadratic equations and functions
Chapter 9 quadratic equations and functions Chapter 8 quadratic functions and equations
Chapter 8 quadratic functions and equations Chapter 3 quadratic equations and complex numbers answers
Chapter 3 quadratic equations and complex numbers answers Log to exponential
Log to exponential Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Exponential equation and inequalities
Exponential equation and inequalities Exponential equation example
Exponential equation example Exponential and logarithmic equations and inequalities
Exponential and logarithmic equations and inequalities Chapter 9 solving quadratic equations
Chapter 9 solving quadratic equations How to graph a quadratic inequality
How to graph a quadratic inequality Unit 2 reasoning with linear equations and inequalities
Unit 2 reasoning with linear equations and inequalities Solving rational equations and inequalities
Solving rational equations and inequalities 8-5 solving rational equations and inequalities
8-5 solving rational equations and inequalities 5-5 solving rational equations and inequalities
5-5 solving rational equations and inequalities How to solve a radical inequality
How to solve a radical inequality Solving radical inequalities
Solving radical inequalities Solving multi step equations and inequalities
Solving multi step equations and inequalities Expressions equations and inequalities unit test
Expressions equations and inequalities unit test Expressions equations and inequalities unit test part 1
Expressions equations and inequalities unit test part 1 How to solve inequalities
How to solve inequalities Equations and inequalities
Equations and inequalities Lesson 7 - graphing radical equations and inequalities
Lesson 7 - graphing radical equations and inequalities