Chapter 1 An Introduction to Business Statistics Mc

Statistics • When it is singular, it refers to the sciences of statistics that help us collect, organize, and interpret Data. • When it is plural, it refers to the data themselves, especially those that describe or summarize something. 1 -2

Populations and Samples Population Variable The set of all elements about which we wish to draw conclusions (usually people, objects or events) Any characteristic of an element is called a variable. Measurement The process of assigning a value of variable to each population unit. Usually it refers to the value itself. 1 -3

Measurement The process of determining the extent, quantity, amount, etc, of the variable of interest for a particular item of the population. • Produces data • For example, collecting annual starting salaries of graduates from last year’s MBA program 1 -4

Quantitative vs. Qualitative(Categorical) Quantitative If the measurements are numbers Qualitative representing how many or how much. If the measurements are attributes, labels, or nonnumeric entries. 1 -5

Quantitative The possible measurements are numbers that represent quantities, ‘how many ’ or ‘how much’ • A person’s weight is quantitative. • A laptop’s price is also quantitative. 1 -6

• When initiating a study, we first define our variable of interest, or response variable. Other variables, called factors, may be related to the response variable interest will also be measured. • When analysts are unable to control the factors of interest, the study is called observational. • If we are able to set or manipulate the values of these factors, we have an experimental study. 1 -7

Qualitative A descriptive category to which a population unit belongs: a descriptive attribute of a population unit. • A person’s gender is qualitative • A person’s hair color is also qualitative 1 -8

Census An examination of the entire population measurements Sample A selected subset of the units of a population 1 -9

Census The process of collecting the population of all measurements is a census. • Census usually too expensive, too time consuming, and too much effort for a large population 1 -10

Sample A subset of population units. • For example, a university graduated 8, 742 students • This is too large for a census • So, we select a sample of these graduates and learn their annual starting salaries 1 -11

Parameter vs. Statistic • A parameter is a numerical description of a population characteristic. Example: the percentage of college students who use Dell computer. • A statistic is a numerical description of a sample characteristic. Example: the percentage of students selected nationwide using Dell computer. 1 -12

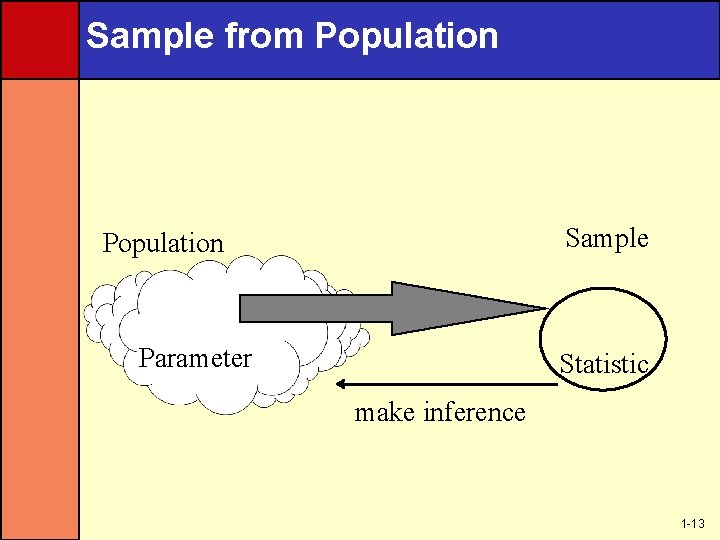
Sample from Population Sample Population Parameter Statistic make inference 1 -13

Descriptive Statistics The science of describing the important aspects of a set of measurements. • For example, for a set of annual starting salaries, want to know: – How much to expect – What is a high versus low salary • If the population is small, could take a census and make statistical inferences • But if the population is too large, then … 1 -14

Statistical Inference The science of using a sample of measurements to make generalizations about the important aspects of a population of measurements. • For example, use a sample of starting salaries to estimate the important aspects of the population of starting salaries 1 -15

Selecting a Random Sample A random sample is a sample selected from a population so that: • Every element in the population has the same chance of being included in the sample. – Each possible sample (of the same size) has the same chance of being selected 1 -16

Random Sample Example • Randomly pick two different people from a group of 15: – Number the people from 1 to 15 and write their numbers on 15 different slips of paper – Thoroughly mix the papers and randomly pick two of them – The numbers on the slips identifies the people for the sample 1 -17

Drawing the Random Sample • If the population is large, use a table of random numbers • In large sampling projects, tables of random numbers are often used to automate the sample selection process • See next slide a table of random numbers 1 -18

Portion of Random Number Table 1 -19

Using Random Number Tables • For a demonstration of the use of random numbers, read Example 1. 1, “Cell Phone Case: Estimating Cell Phone Costs, ” in the textbook • Use random numbers to randomly select 100 employees from a bank with 2, 136 employees • Random numbers can be computer-generated 1 -20

Approximately Random Samples • In general, must make a list identifying each and every individual population unit – Called a frame • If the population is very large, it may not be possible to list every individual population unit • So instead draw a “systematic” sample 1 -21

Systematic Sample • Randomly enter the population and systematically sample every kth unit • This usually approximates a random sample – Read Example 1. 2, “Marketing Research Case: Rating a New Bottle Design, ” in the textbook 1 -22

Systematic Sampling • Select some starting point and then select every k th element in the population 1 -23

Example 1. 2: Rating a New Bottle Design • Wish to determine consumer reaction to a new bottle design • Will use the “mall intercept method” – Shoppers in a mall are intercepted and asked to participate in a consumer survey • Asked to rate a new bottle 1 -24

Example 1. 2: Using Systematic Sample • Cannot list and number every shopper – As a result, cannot use random numbers • Instead, will use a systematic sample • Every 100 th shopper is selected – Using every 100 th shopper is arbitrary • Using widely spaced shoppers, can be reasonable sure not related 1 -25

Problems With Non-Random Samples • For presidential election of 1936, Literary Digest predicted Alf Landon would defeat Franklin D. Roosevelt • Instead Roosevelt won in a landslide • Literary Digest’s mistake was to sample names from telephone books and club membership rosters • Many people did not have phones or belong to clubs – As a result, they were not included in sample – They voted overwhelmingly for Roosevelt 1 -26

Voluntary Response Sample • Participants select themselves to be in the sample – Participants “self-select” – For example, voting on American Idol – Commonly referred to as a “non-scientific” sample • Usually not representative of the population – Over-represent individuals with strong opinions – Usually, but not always, negative opinions 1 -27

Terminology • Measurement • Quantitative • Qualitative • Population of Measurement • Census • Sample • Random Sample • Descriptive Statistics • Statistical Inference 1 -28

• http: //www. learner. org/vod_window. html? pid=139 • http: //www. learner. org/vod_window. html? pid=152 1 -29