CHAPTER 1 A INFORMATION CAPACITY AND NOISE n

CHAPTER 1 A INFORMATION CAPACITY AND NOISE

n n The two most significant limitations on the performance of a communications system are Noise and Bandwidth of an information signal is simply the difference between the highest and the lowest frequencies contained in the information. The bandwidth of a communication channel is the difference between the highest and the lowest frequencies that the channel will allow to pass through (e. g. passband). Therefore, the bandwidth of the communication channel must be equal to or greater than the bandwidth of the information.

n For example, voice frequencies contain signals between 300 Hz and 3000 Hz. Therefore, a voice-frequency channel must have a bandwidth equal to or greater than 2700 Hz (300 Hz-3000 Hz).

Information Capacity Information capacity is a measure of how much information can be propagated through a communication system. n Information capacity represents the number of independent symbols that can be carried through a system in a given unit of time. n The most basic digital symbol used to represent information is the binary digit or bit. n

Information Capacity n

n

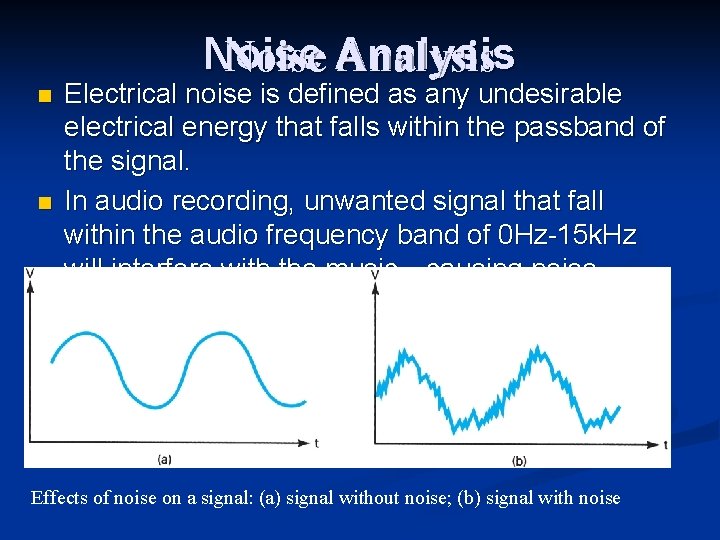
Noise Analysis n n Electrical noise is defined as any undesirable electrical energy that falls within the passband of the signal. In audio recording, unwanted signal that fall within the audio frequency band of 0 Hz-15 k. Hz will interfere with the music—causing noise. Effects of noise on a signal: (a) signal without noise; (b) signal with noise

Noise Analysis n n n Two categories: Correlated and Uncorrelated Noise Correlated noise exist only when signal is present Uncorrelated noise present at all time whethere is a signal or not. Uncorrelated noise can be external or internal. External noise is generated outside the device/circuit. Ø Atmospheric noise-originate with earth atmosphere, static electricity (crackling, sputtering of speaker) when there is no signal present.

Man-made noise – spark-producing mechanism, e. g. commutators in electric motor, fluorescent lights, etc. Internal Noise- electrical interference generated within a device/circuit. Ø Shot noise- caused by random arrival of carriers (holes and electrons), e. g. diode, transistors Ø Transit-time noise – carriers travelling from emitter to collector suffer from emitter-time delay, propagation time delay, etc. Ø Thermal noise – rapid and random movement of electron due to thermal agitation. Ø §

Thermal Noise Power n

n

n Thermal noise is equally distributed throughout the frequency spectrum. It is also called white noise which is analogous to white light which contains all visible-light frequencies. Noise source equivalent circuit

Example: For an electronic device operating at a temperature of 17 o. C with a bandwidth of 10 k. Hz, determine (a) Thermal noise power (b) rms noise voltage for a 100 internal resistance and a 100 external load resistance. n

Solution: (a) N=(1. 38 x 10 -23)(290)(1 x 104)=4 x 10 -17 W (b)

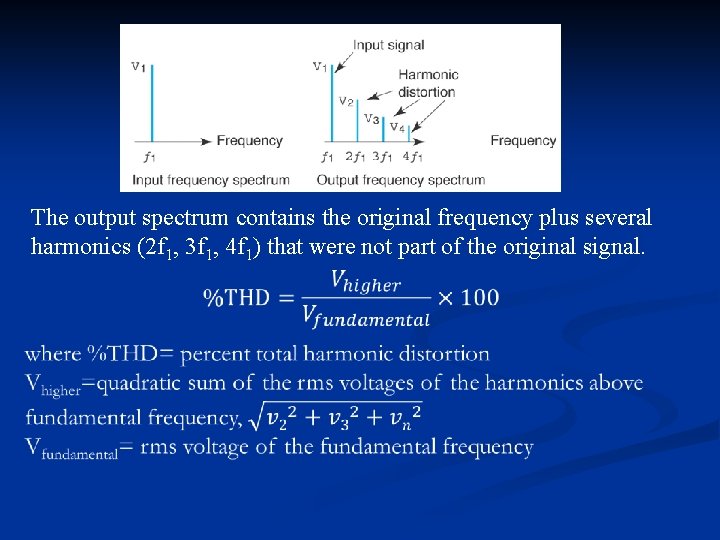
Correlated Noise n n Correlated noise is produced by nonlinear amplification which includes harmonic distortion and intermodulation distortion. Harmonics are integer multiples of original signal (fundamental frequency or first harmonic). A frequency two times the original frequency is the second harmonic, three times is the third harmonic and so forth. nth order harmonic distortion is the ratio of rms amplitude of the nth harmonic to the rms amplitude of the fundamental.

The output spectrum contains the original frequency plus several harmonics (2 f 1, 3 f 1, 4 f 1) that were not part of the original signal.

Example: Determine (a) 2 nd, 3 rd, and 12 th harmonics for a 1 k. Hz repetitive wave (b) Percent of second-order, third-order, and total harmonic distortion for a fundamental frequency with an amplitude of 8 Vrms, a second harmonic amplitude of 0. 2 Vrms, and a third harmonic amplitude of 0. 1 Vrms. n Solution: (a) 2 nd harmonic= 2 x fundamental=2 x 1= 2 k. Hz 3 rd harmonic= 3 x fundamental=3 x 1= 3 k. Hz 12 th harmonic= 12 x fundamental=12 x 1= 12 k. Hz

n

n

For a nonlinear amplifier with two input frequencies, 3 k. Hz and 8 k. Hz, determine (a) First three harmonics present in the output for each input frequency. (b) Cross-product frequencies produced for values of m and n of 1 and 2. Solution: (a) Two times each of the original frequencies: 6 Hz and 16 Hz, and three times each of the original frequencies: 9 k. Hz and 24 k. Hz. n

(b) m n Cross Products 1 1 8± 3= 5 k. Hz and 11 k. Hz 1 2 8± 6= 2 k. Hz and 14 k. Hz 2 1 16± 3= 13 k. Hz and 19 k. Hz 2 2 16± 6= 10 k. Hz and 22 k. Hz

Electrical Interference happens when information signals from one source produce frequencies that fall outside their allocated bandwidth and interfere with information signal from another source. n E. g. CB radios transmit signals in 27 MHz to 28 MHz. Their second harmonic (5455 MHz) fall within the band allocated to VHF television channel. If the radio signals that produce high-amplitude second harmonic are transmitted, it could interfere other people’s TV reception. n

Signal to noise power ratio • • Signal to noise power ratio: the ratio of the signal power level to the noise power level. Is expressed as: Where : Ps=Signal power (watts) Pn=Noise power (watts) • Normally expressed as logarithmic function with the decibel unit.

n In terms of voltages and resistances: Where : Rin =input resistance Rout=output resistance Vs =signal voltage Vn =noise voltage n If the input and output resistances are equal in a system, then:

n

n

Noise factor and Noise Figure • Noise Factor (F) and Noise Figure (NF) are figures of merit used to indicate how much the signal-to-noise ratio deteriorates as a signal passes through a circuit or series of circuits. • Noise factor (F) : a ratio of input signal-tonoise power ratio to output signal-to-noise power ratio.

• Noise Figure (NF) : the noise factor stated in d. B. This parameter commonly used to indicate the quality of a receiver. • In simple word, the Noise Figure is the noise factor, given in d. B. • These formulae only valid when the input termination is at standard noise temperature, To=290 K.

Noise factor and Noise Figure

Example 3: For a nonideal amplifier and the following parameters, determine: i) Input signal to noise ratio (d. B) ii) Output signal to noise ratio (d. B) iii) Noise factor & noise figure input signal power = 2 x 10 -10 W input noise power = 2 x 10 -18 W power gain = 1 x 106 internal noise = 6 x 10 -12 W

Solution : i) Input S/N ratio : Output S/N ratio: - Find output noise power : ii)

Solution : - Find output signal power : - Find output S/N :

Solution : iii) Noise factor : Noise Figure : NF= 10 log F = 6 d. B

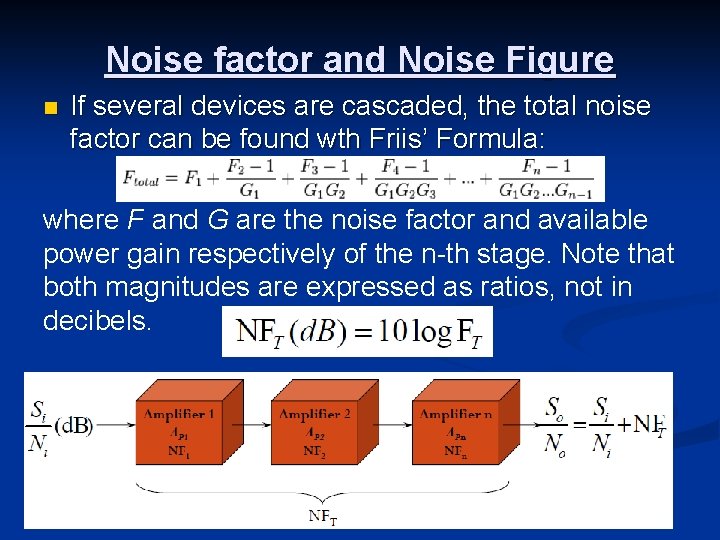
Noise factor and Noise Figure n If several devices are cascaded, the total noise factor can be found wth Friis’ Formula: where F and G are the noise factor and available power gain respectively of the n-th stage. Note that both magnitudes are expressed as ratios, not in decibels.

Example 4: For three cascaded amplifier stage, each with noise figure of 3 d. B and power gains of 10 d. B, determine the total noise figure. Solution: Convert noise figure, NF to noise factor, F: Using Friis’ Formula:

Observations from the example: n The overall noise figure (3. 24 d. B) was not significantly larger than noise figure of the first stage. n The first stage contributes the most to the overall noise figure. n This is true as long as the gain of the first stage is sufficient to reduce the effect of the succeeding stages. n

Equivalent Noise Temperature n

Example: n Determine (a) Noise figure for an equivalent noise temperature of 75 K n (b) Equivalent noise temperature for a noise figure of 6 d. B. n

n

Exercises: A mixer stage has a noise figure of 20 d. B, and this is preceded by an amplifier that has a noise figure of 9 d. B and an available power gain of 15 d. B. Calculate the overall noise figure referred to the input. n

n