Chapter 03 Macroscopic interface dynamics Part A physical

Chapter 03: Macroscopic interface dynamics Part A: physical and mathematical modeling of interface Xiangyu Hu Technical University of Munich

Basic equations (1) • Continuity equation – Integral form – Derivative form – Form with substantial derivatives Substantial derivative

Basic equations (2) • Momentum equation – Integral form – Derivative form – Form with substantial derivatives Stress tensor • Equation of state

Incompressible flows (1) • Continuity equation or • Momentum equation Kinematic viscosity

Incompressible flows (2) • Boundary conditions – No-slip – Finite slip Shear rate along normal direction

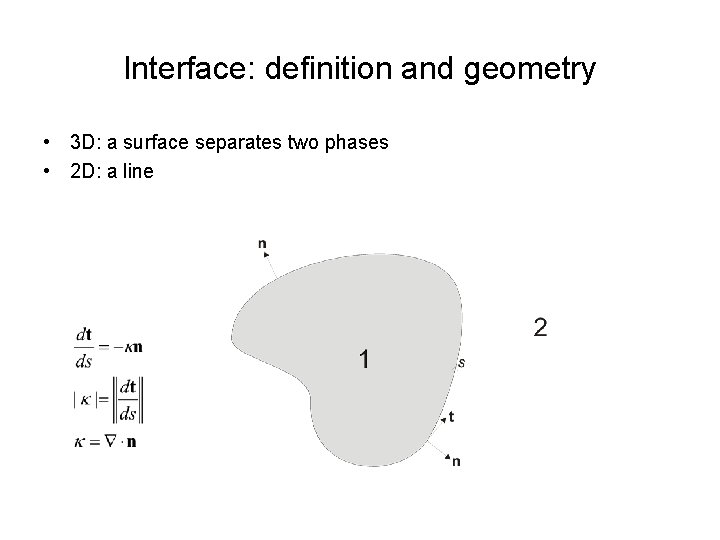
Interface: definition and geometry • 3 D: a surface separates two phases • 2 D: a line

Mathematical representation of a 2 D interface • Implicit function • Characteristic function – H=0 in phase 1 and H=1 in phase 2 – 2 D Heaviside step function • Distribution concentrated on interface – Dirac function d. S normal to interface – Gradient of H Change volume integrals into surface integrals • Interface motion

Fluid mechanics with interfaces (1) • Mass conservation and velocity condition – Without phase change • Velocity continuous along normal direction • Interface velocity equal to fluid velocity along normal direction – With phase change • Velocity discontinuous along normal direction – Rankine-Hugoniot condition

Fluid mechanics with interfaces (2) • Momentum conservation and surface tension and Marangoni effects • Split form along normal and tangential direction Shear rate tensor Derivative of surface tension along the interface

Momentum equation including surface effects (1) • Integral form – With surface integral on interface – With volume integral on fluids

Momentum equation including surface effects (2) • Derivative form – With surface force – With surface stress • Usually constant surface tension considered