Chapter 0 Functions GoldsteinSchneiderLayAsmar Calculus and Its Applications



































![Dividing Functions EXAMPLE Given and , express [f (x)]/[g (x)] as a rational function. Dividing Functions EXAMPLE Given and , express [f (x)]/[g (x)] as a rational function.](https://slidetodoc.com/presentation_image/93bdfb9106fa3d97f0224852022ef4a7/image-39.jpg)






































- Slides: 78

Chapter 0 Functions Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 1

Chapter Outline q Functions and Their Graphs q Some Important Functions q The Algebra of Functions q Zeros of Functions – The Quadratic Formula and Factoring q Exponents and Power Functions q Functions and Graphs in Applications Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 2

§ 0. 1 Functions and Their Graphs Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 3

Section Outline q Rational and Irrational Numbers q The Number Line q Open and Closed Intervals q Applications of Functions q Domain of a Function q Graphs of Functions q The Vertical Line Test q Graphing Calculators q Graphs of Equations Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 4

Rational & Irrational Numbers Definition Example Rational Number: A number that may be written as a finite or infinite repeating decimal, in other words, a number that can be written in the form m/n such that m, n are integers Irrational Number: A number that has an infinite decimal representation whose digits form no repeating pattern Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 5

The Number Line A geometric representation of the real numbers is shown below. -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 6

Open & Closed Intervals Definition Open Interval: The set of numbers that lie between two given endpoints, not including the endpoints themselves Closed Interval: The set of numbers that lie between two given endpoints, including the endpoints themselves Example -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 [-1, 4] Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 7

Functions in Application EXAMPLE (Response to a Muscle) When a solution of acetylcholine is introduced into the heart muscle of a frog, it diminishes the force with which the muscle contracts. The data from experiments of the biologist A. J. Clark are closely approximated by a function of the form where x is the concentration of acetylcholine (in appropriate units), b is a positive constant that depends on the particular frog, and R(x) is the response of the muscle to the acetylcholine, expressed as a percentage of the maximum possible effect of the drug. (a) Suppose that b = 20. Find the response of the muscle when x = 60. (b) Determine the value of b if R(50) = 60 – that is, if a concentration of x = 50 units produces a 60% response. SOLUTION (a) This is the given function. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 8

Functions in Application CONTINUED Replace b with 20 and x with 60. Simplify the numerator and denominator. Divide. Therefore, when b = 20 and x = 60, R (x) = 75%. (b) This is the given function. Replace x with 50. Replace R(50) with 60. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 9

Functions in Application CONTINUED Simplify the numerator. Multiply both sides by b + 50 and cancel. Distribute on the left side. Subtract 3000 from both sides. Divide both sides by 60. Therefore, when R (50) = 60, b = 33. 3. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 10

Functions EXAMPLE If , find f (a - 2). SOLUTION This is the given function. Replace each occurrence of x with a – 2. Evaluate (a – 2)2 = a 2 – 4 a + 4. Remove parentheses and distribute. Combine like terms. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 11

Domain Definition Domain of a Function: The set of acceptable values for the variable x. Example The domain of the function is Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 12

Graphs of Functions Definition Example Graph of a Function: The set of all points (x, f (x)) where x is the domain of f (x). Generally, this forms a curve in the xyplane. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 13

The Vertical Line Test Definition Example Vertical Line Test: A curve in the xy-plane is the graph of a function if and only if each vertical line cuts or touches the curve at no more than one point. Although the red line intersects the graph no more than once (not at all in this case), there does exist a line (the yellow line) that intersects the graph more than once. Therefore, this is not the graph of a function. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 14

Graphing Calculators Graphing Using a Graphing Calculator Step Display 1) Enter the expression for the function. 2) Enter the specifications for the viewing window. 3) Display the graph. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 15

Graphs of Equations EXAMPLE Is the point (3, 12) on the graph of the function ? SOLUTION This is the given function. Replace x with 3. Replace f (3) with 12. Simplify. false Multiply. Since replacing x with 3 and f (x) with 12 did not yield a true statement in the original function, we conclude that the point (3, 12) is not on the graph of the function. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 16

§ 0. 2 Some Important Functions Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 17

Section Outline q Linear Equations q Applications of Linear Functions q Piece-Wise Functions q Quadratic Functions q Polynomial Functions q Rational Functions q Power Functions q Absolute Value Function Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 18

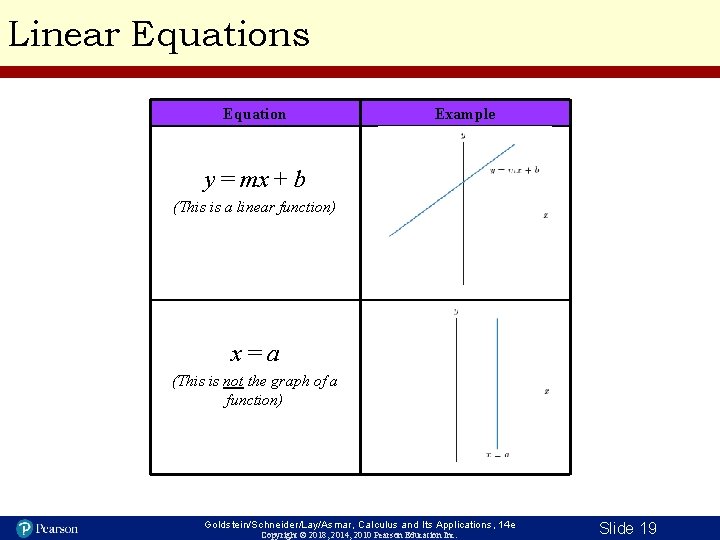
Linear Equations Equation Example y = mx + b (This is a linear function) x=a (This is not the graph of a function) Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 19

Linear Equations CONTINUED Equation Example y=b In this case, f(x) is called a constant function, since it assigns the same number b to every value of x Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 20

Applications of Linear Functions EXAMPLE (Enzyme Kinetics) In biochemistry, such as in the study of enzyme kinetics, one encounters a linear function of the form , where K and V are constants. (a) If f (x) = 0. 2 x + 50, find K and V so that f (x) may be written in the form, (b) Find the x-intercept and y-intercept of the line . in terms of K and V. SOLUTION (a) Since the number 50 in the equation f (x) = 0. 2 x + 50 is in place of the term 1/V (from the original function), we know the following. 50 = 1/V 50 V = 1 V = 0. 02 Explained above. Multiply both sides by V. Divide both sides by 50. Now that we know what V is, we can determine K. Since the number 0. 2 in the equation (x) = 0. 2 x + 50 is in place of K/V (from the original function), we know the following. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 21 f

Applications of Linear Functions CONTINUED 0. 2 = K/V 0. 2 V = K 0. 2(0. 02) = K 0. 004 = K Explained above. Multiply both sides by V. Replace V with 0. 02. Multiply. Therefore, in the equation f (x) = 0. 2 x + 50, K = 0. 004 and V = 0. 02. (b) To find the x-intercept of the original function, replace f (x) with 0. This is the original function. Replace f (x) with 0. Solve for x by first subtracting 1/V from both sides. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 22

Applications of Linear Functions CONTINUED Multiply both sides by V/K. Simplify. Therefore, the x-intercept is -1/K. To find the y-intercept of the original function, we recognize that this equation is in the form y = mx + b. Therefore we know that 1/V is the y-intercept. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 23

Piece-Wise Functions EXAMPLE Sketch the graph of the following function . SOLUTION We graph the function f (x) = 1 + x only for those values of x that are less than or equal to 3. Notice that for all values of x greater than 3, there is no line. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 24

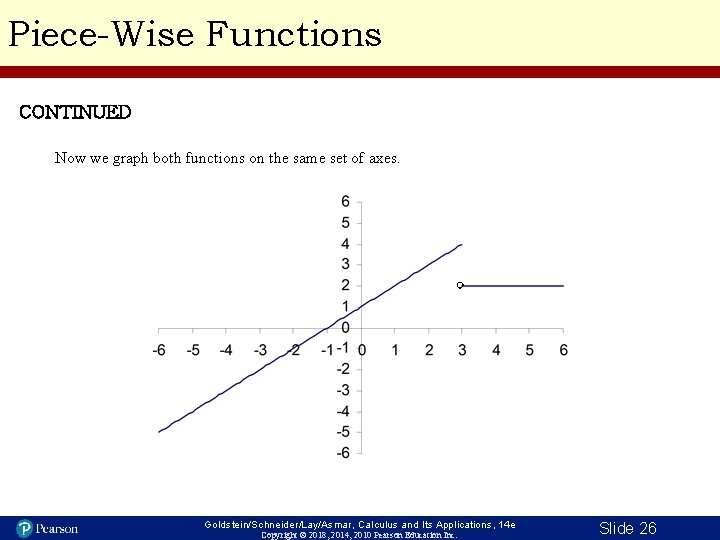
Piece-Wise Functions CONTINUED Now we graph the function f (x) = 4 only for those values of x that are greater than 3. Notice that for all values of x less than or equal to 3, there is no line. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 25

Piece-Wise Functions CONTINUED Now we graph both functions on the same set of axes. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 26

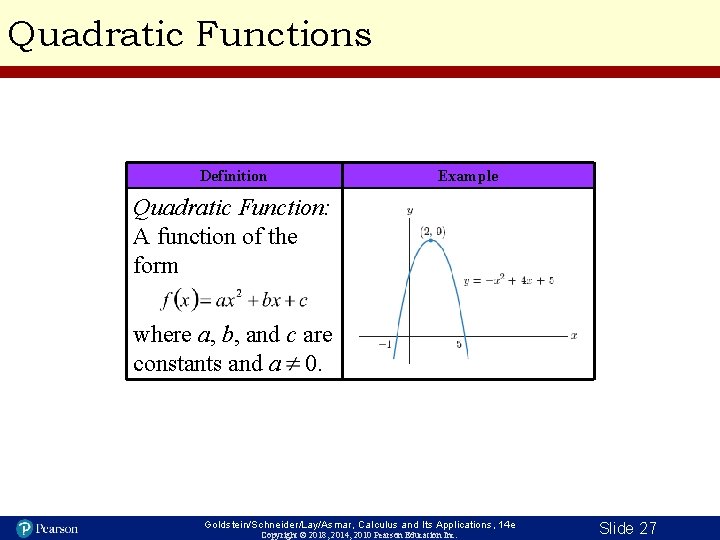
Quadratic Functions Definition Example Quadratic Function: A function of the form where a, b, and c are constants and a 0. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 27

Polynomial Functions Definition Example Polynomial Function: A function of the form where n is a nonnegative integer and a 0, a 1, . . . an are given numbers. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 28

Rational Functions Definition Example Rational Function: A function expressed as the quotient of two polynomials. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 29

Power Functions Definition Example Power Function: A function of the form Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 30

Absolute Value Function Definition Example Absolute Value Function: The function defined for all numbers x by such that |x| is understood to be x if x is positive and –x if x is negative Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 31

§ 0. 3 The Algebra of Functions Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 32

Section Outline q Adding Functions q Subtracting Functions q Multiplying Functions q Dividing Functions q Composition of Functions Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 33

Adding Functions EXAMPLE Given and , express f (x) + g (x) as a rational function. SOLUTION f (x) + g (x) = Replace f (x) and g (x) with the given functions. Multiply to get common denominators. Evaluate. Add. Simplify the numerator. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 34

Adding Functions CONTINUED Evaluate the denominator. Simplify the denominator. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 35

Subtracting Functions EXAMPLE Given and , express f (x) - g (x) as a rational function. SOLUTION f (x) - g (x) = Replace f (x) and g (x) with the given functions. Multiply to get common denominators. Evaluate. Subtract. Simplify the numerator. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 36

Subtracting Functions CONTINUED Evaluate the denominator. Simplify the denominator. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 37

Multiplying Functions EXAMPLE Given and , express f (x)g (x) as a rational function. SOLUTION f (x)g (x) = Replace f (x) and g (x) with the given functions. Multiply the numerators and denominators. Evaluate. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 38
![Dividing Functions EXAMPLE Given and express f xg x as a rational function Dividing Functions EXAMPLE Given and , express [f (x)]/[g (x)] as a rational function.](https://slidetodoc.com/presentation_image/93bdfb9106fa3d97f0224852022ef4a7/image-39.jpg)
Dividing Functions EXAMPLE Given and , express [f (x)]/[g (x)] as a rational function. SOLUTION f (x)/g (x) = Replace f (x) and g (x) with the given functions. Rewrite as a product (multiply by reciprocal of denominator). Multiply the numerators and denominators. Evaluate. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 39

Composition of Functions EXAMPLE (Conversion Scales) Table 1 shows a conversion table for men’s hat sizes for three countries. The function converts from British sizes to French sizes, and the function converts from French sizes to U. S. sizes. Determine the function h (x) = f (g (x)) and give its interpretation. SOLUTION h (x) = f (g (x)) This is what we will determine. In the function f, replace each occurrence of x with g (x). Replace g (x) with 8 x + 1. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 40

Composition of Functions CONTINUED Distribute. Multiply. Therefore, h (x) = f (g (x)) = x + 1/8. Now to determine what this function h (x) means, we must recognize that if we plug a number into the function, we may first evaluate that number plugged into the function g (x). Upon evaluating this, we move on and evaluate that result in the function f (x). This is illustrated as follows. g (x) British f (x) French U. S. h (x) Therefore, the function h (x) converts a men’s British hat size to a men’s U. S. hat size. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 41

§ 0. 4 Zeros of Functions – The Quadratic Formula and Factoring Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 42

Section Outline q Zeros of Functions q Quadratic Formula q Graphs of Intersecting Lines q Factoring Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 43

Zeros of Functions Definition Example Zero of a Function: For a function f (x), all values of x such that f (x) = 0. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 44

Quadratic Formula Definition Example Quadratic Formula: A formula for solving any quadratic equation of the form. The solution is: There is no solution if These are the solutions/zeros of the quadratic function Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 45

Graphs of Intersecting Functions EXAMPLE Find the points of intersection of the pair of curves. SOLUTION The graphs of the two equations can be seen to intersect in the following graph. We can use this graph to help us to know whether our final answer is correct. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 46

Graphs of Intersecting Functions CONTINUED To determine the intersection points, set the equations equal to each other, since they both equal the same thing: y. Now we solve the equation for x using the quadratic formula. This is the equation to solve. Subtract x from both sides. Add 9 to both sides. We now recognize that, for the quadratic formula, a = 1, b = -11, and c =18. Use the quadratic formula. Simplify. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 47

Graphs of Intersecting Functions CONTINUED Simplify. Rewrite. Simplify. We now find the corresponding y-coordinates for x = 9 and x = 2. We can use either of the original equations. Let’s use y = x – 9. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 48

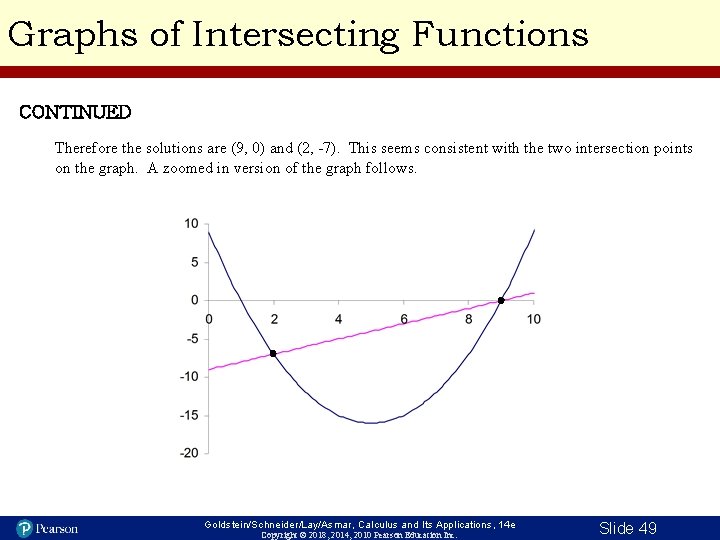
Graphs of Intersecting Functions CONTINUED Therefore the solutions are (9, 0) and (2, -7). This seems consistent with the two intersection points on the graph. A zoomed in version of the graph follows. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 49

Factoring EXAMPLE Factor the following quadratic polynomial. SOLUTION This is the given polynomial. Factor 2 x out of each term. Rewrite 3 as Now I can use the factorization pattern: a 2 – b 2 = (a – b)(a + b). Rewrite Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 50

Factoring EXAMPLE Solve the equation for x. SOLUTION This is the given equation. Multiply everything by the LCD: x 2. Distribute. Multiply. Subtract 5 x + 6 from both sides. Factor. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 51

Factoring CONTINUED Set each factor equal to zero. Solve. Since no denominator from the original equation is zero when x = -1 or when x = 6, these are our solutions. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 52

§ 0. 5 Exponents and Power Functions Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 53

Section Outline q Exponent Rules q Applications of Exponents q Compound Interest Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 54

Exponents Definition Example Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 55

Exponents Definition Example Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 56

Exponents Definition Example Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 57

Exponents Definition Example Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 58

Exponents Definition Example Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 59

Applications of Exponents EXAMPLE Use the laws of exponents to simplify the algebraic expression. SOLUTION This is the given expression. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 60

Applications of Exponents CONTINUED Subtract. Divide. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 61

Compound Interest - Annual Definition Compound Interest Formula: Example If $700 is invested, compounded annually at 8% for 8 years, this will grow to: A = the compound amount (how much money you end up with) P = the principal amount invested i = the compound interest rate per interest period Therefore, the compound amount n = the number of would be $1, 295. 65. compounding periods Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 62

Compound Interest - General Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 63

Compound Interest - General EXAMPLE (Quarterly Compound) Assume that a $500 investment earns interest compounded quarterly. Express the value of the investment after one year as a polynomial in the annual rate of interest r. SOLUTION Since interest is not being compounded annually, we must use this formula. Replace P with 500, m with 4 (interest is compounded 4 times each year), and t with 1 (interest is being compounded for 1 year). Simplify. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 64

§ 0. 6 Functions and Graphs in Application Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 65

Section Outline q Geometric Problems q Cost, Revenue, and Profit q Surface Area q Functions and Graphs Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 66

Geometric Problems EXAMPLE (Fencing a Rectangular Corral) Consider a rectangular corral with two partitions, as shown below. Assign letters to the outside dimensions of the corral. Write an equation expressing the fact that the corral has a total area of 2500 square feet. Write an expression for the amount of fencing needed to construct the corral (including both partitions). SOLUTION First we will assign letters to represent the dimensions of the corral. y x x y Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 67

Geometric Problems CONTINUED Now we write an equation expressing the fact that the corral has a total area of 2500 square feet. Since the corral is a rectangle with outside dimensions x and y, the area of the corral is represented by: Now we write an expression for the amount of fencing needed to construct the corral (including both partitions). To determine how much fencing will be needed, we add together the lengths of all the sides of the corral (including the partitions). This is represented by: Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 68

Cost Problems EXAMPLE (Cost of Fencing) Consider the corral of the last example. Suppose the fencing for the boundary of the corral costs $10 per foot and the fencing for the inner partitions costs $8 per foot. Write an expression for the total cost of the fencing. SOLUTION This is the diagram we drew to represent the corral. y x x y Since the boundary of the fence is represented by the red part of the diagram, the length of fencing for this portion of the corral is x + y + y = 2 x + 2 y. Therefore the cost of fencing the boundary of the fence is (2 x + 2 y)(cost of boundary fencing per foot) = (2 x + 2 y)(10) = 20 x + 20 y. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 69

Cost Problems CONTINUED Since the inner partitions of the fence are represented by the blue part of the diagram, the length of fencing for this portion of the corral is x + x = 2 x. Therefore the cost of fencing the inner partitions of the fence is (2 x)(cost of inner partition fencing per foot) = (2 x)(8) = 16 x. Therefore, an expression for the total cost of the fencing is: (cost of boundary fencing) + (cost of inner partition fencing) (20 x + 20 y) + (16 x) 36 x + 20 y Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 70

Surface Area EXAMPLE Assign letters to the dimensions of the geometric box and then determine an expression representing the surface area of the box. SOLUTION First we assign letters to represent the dimensions of the box. z y x Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 71

Surface Area CONTINUED z y x Now we determine an expression for the surface area of the box. Note, the box has 5 sides which we will call Left (L), Right (R), Front (F), Back (B), and Bottom (Bo). We will find the area of each side, one at a time, and then add them all up. L: yz R: yz F: xz Bo: xy Therefore, an expression that represents the surface area of the box is: yz + xz + xy = 2 yz +2 xz +xy. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 72

Cost, Revenue, & Profit EXAMPLE (Cost, Revenue, and Profit) An average sale at a small florist shop is $21, so the shop’s weekly revenue function is R(x) = 21 x where x is the number of sales in 1 week. The corresponding weekly cost is C(x) = 9 x + 800 dollars. (a) What is the florist shop’s weekly profit function? (b) How much profit is made when sales are at 120 per week? (c) If the profit is $1000 for a week, what is the revenue for the week? SOLUTION (a) Since Profit = Revenue – Cost, the profit function, P(x), would be: P(x) = R(x) – C(x) P(x) = 21 x – (9 x + 800) P(x) = 21 x – 9 x - 800 P(x) = 12 x - 800 Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 73

Cost, Revenue, & Profit CONTINUED (b) Since x represents the number of sales in one week, to determine how much profit is made when sales are at 120 per week, we will replace x with 120 in the profit function and then evaluate. P(120) = 12(120) - 800 P(120) = 1, 440 - 800 P(120) = 640 Therefore, when sales are at 120 per week, profit is $640 for that week. (c) To determine the revenue for the week when the profit is $1000 for that week, we use an equation that contains profit, namely the profit function: P(x) = 12 x - 800 Now we replace P(x) with 1000 and solve for x. 1000 = 12 x - 800 1800 = 12 x 150 = x Therefore x, the number of units sold in a week, is 150 when profit is $1000. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 74

Cost, Revenue, & Profit CONTINUED Now, to determine the corresponding revenue, we replace x with 150 in the revenue function. R(x) = 21 x R(150) = 21(150) R(150) = 3, 150 Therefore, when profit is $1000 in a week, the corresponding revenue is $3, 150. NOTE: In order to determine the desired revenue value in part (c), we needed to solve for R(x). But in order to do that, we needed to have a value for x to plug into the R(x) function. In order to acquire that value for x, we needed to use the given information – profit is $1000. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 75

Functions & Graphs EXAMPLE The function f (r) gives the cost (in cents) of constructing a 100 -cubic-inch cylinder of radius r inches. The graph of f (r) is given. (a) What is the cost of constructing a cylinder of radius 6 inches? (b) Interpret the fact that the point (3, 162) is on the graph of the function. (c) Interpret the fact that the point (3, 162) is the lowest point on the graph of the function. What does this say in terms of cost versus radius? Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 76

Functions & Graphs CONTINUED SOLUTION To determine the cost of constructing a cylinder of radius 6 inches, we look on the graph where r = 6. The corresponding y value will be the cost we are seeking. The red arrow is emphasizing the point in which we are interested. The y value of that point is 270. Therefore, the cost of constructing a cylinder of radius 6 inches is 270 cents or $2. 70. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 77

Functions & Graphs CONTINUED (b) The fact that the point (3, 162) is on the graph tells us that the cost to make 100 -cubic-inch cylinders with a radius as small as 3 inches is 162 cents or $1. 62. (c) The fact that the point (3, 162) is the lowest point on the graph tells us that the least expensive 100 -cubic-inch cylinder that can be made is a 3 inch cylinder at a cost of $1. 62. Therefore, the 3 inch cylinder is the most cost-effective one that is offered. Goldstein/Schneider/Lay/Asmar, Calculus and Its Applications, 14 e Copyright © 2018, 2014, 2010 Pearson Education Inc. Slide 78
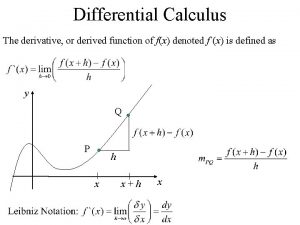
 Pre ap precalculus
Pre ap precalculus Differential calculus functions
Differential calculus functions Functions from a calculus perspective
Functions from a calculus perspective Oscilloscope working
Oscilloscope working The fourier transform and its applications
The fourier transform and its applications Daniel spielman spectral graph theory
Daniel spielman spectral graph theory Spectral graph theory and its applications
Spectral graph theory and its applications Linear algebra and its applications
Linear algebra and its applications The resistance r experienced by a partially submerged body
The resistance r experienced by a partially submerged body Fast random walk with restart and its applications
Fast random walk with restart and its applications Slater's rule
Slater's rule Cstnet
Cstnet Clientserver architecture
Clientserver architecture Kohlrausch law
Kohlrausch law Calculus chapter 2 limits and continuity
Calculus chapter 2 limits and continuity Zener diode and its application
Zener diode and its application The emigree analysis
The emigree analysis Its halloween its halloween the moon is full and bright
Its halloween its halloween the moon is full and bright Calculus chapter 5
Calculus chapter 5 Stewart
Stewart Ap calculus chapter 5
Ap calculus chapter 5 Honors precalculus chapter 1 test
Honors precalculus chapter 1 test Calculus chapter 3
Calculus chapter 3 Calculus chapter 12
Calculus chapter 12 Chapter p preparation for calculus
Chapter p preparation for calculus What is calculus for
What is calculus for Real life piecewise function word problems
Real life piecewise function word problems Applications of cubic functions
Applications of cubic functions Importance of money
Importance of money Management and its functions
Management and its functions What is unit of account example
What is unit of account example When a train increases its velocity its momentum
When a train increases its velocity its momentum Windy cloudy rainy sunny
Windy cloudy rainy sunny If its a square it's a sonnet summary
If its a square it's a sonnet summary Its not easy but its worth it
Its not easy but its worth it Evaluating functions
Evaluating functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Chapter 3 skills and applications
Chapter 3 skills and applications Chapter 6 skills and applications
Chapter 6 skills and applications Principles of economics chapter 28 answers
Principles of economics chapter 28 answers Chapter 2 skills and applications
Chapter 2 skills and applications Relational algebra and calculus
Relational algebra and calculus Tuple and domain calculus collectively known as
Tuple and domain calculus collectively known as Relational algebra to tuple relational calculus
Relational algebra to tuple relational calculus Thomas calculus limits and continuity
Thomas calculus limits and continuity The relational calculus is considered as
The relational calculus is considered as Expressive power of algebra and calculus
Expressive power of algebra and calculus Relational calculus
Relational calculus Debris index score
Debris index score Relational algebra and relational calculus
Relational algebra and relational calculus Piecewise functions absolute value
Piecewise functions absolute value Chapter 23:1 performing range of motion exercises
Chapter 23:1 performing range of motion exercises Chapter 8 linear programming applications solutions
Chapter 8 linear programming applications solutions Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Line regulation
Line regulation Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Whats vietnamization
Whats vietnamization Chapter 11 energy and its conservation answers
Chapter 11 energy and its conservation answers A 1875 kg car going 23 m/s
A 1875 kg car going 23 m/s Chapter 12 reconstruction
Chapter 12 reconstruction Chapter 11 energy and its conservation answers
Chapter 11 energy and its conservation answers A 1875 kg car going 23 m/s
A 1875 kg car going 23 m/s Which is represented by the equation fδt = pf - pi ?
Which is represented by the equation fδt = pf - pi ? Chapter 17 manifest destiny and its legacy
Chapter 17 manifest destiny and its legacy Chapter 1 risk and its treatment
Chapter 1 risk and its treatment Chapter 5 elasticity and its application multiple choice
Chapter 5 elasticity and its application multiple choice Chapter 12 reconstruction and its effects
Chapter 12 reconstruction and its effects Chapter 3 section 1 england and its colonies
Chapter 3 section 1 england and its colonies Application of heat transfer
Application of heat transfer Image sets
Image sets Ap calculus ab jeopardy
Ap calculus ab jeopardy Shell method
Shell method Vector calculus examples
Vector calculus examples Uva calculus placement test
Uva calculus placement test What trig functions are positive in quadrant 2
What trig functions are positive in quadrant 2 Theories of mineralisation
Theories of mineralisation History of calculus timeline
History of calculus timeline Ftoc2
Ftoc2 Fundamental theorem
Fundamental theorem