CHAPITRE III LA LIAISON CHIMIQUE LES MOLCULES 1

CHAPITRE III LA LIAISON CHIMIQUE LES MOLÉCULES

1 - DÉFINITION On appelle liaison chimique le phénomène qui décrit le fait que des noyaux, entités de charge positive, sont astreints à rester dans une même zone de l'espace; la distance les séparant étant de quelques Angöstroms. Cette situation n'est possible que si des électrons (au moins un) sont en interaction avec ces noyaux. La position d'équilibre est régie par l'ensemble des interactions, d'origine électromagnétique, attractives ou répulsives des charges en présence. Seuls les électrons de valence des atomes voisins contribuent à la formation de la liaison chimique, les électrons du cœur "suivent" le noyau et restent sous sa seule influence. C'est pour cette raison qu'on dit que la liaison chimique est établie entre les atomes.

I’ION MOLÉCULAIRE H 2 + La liaison chimique la plus simple est contactée entre deux protons et un électron; c'est l'ion moléculaire H. La résolution exacte de l'équation de Schrödinger de l'ion moléculaire H 2+ fait dans le système de coordonnées elliptiques. On obtient ainsi les expression des fonctions d'onde et de leur énergie. RÉSOLUTION APPROCHÉE Le mouvement de l'électron est décrit par une fonction d'onde moléculaire i, combinaison linéaire des orbitales atomiques d'atomes d'hydrogènes notées fq et supposées normées: La fonction d'onde i est une fonction d'onde monoélectronique. Elle porte le nom d'orbitale moléculaire. Elle est construite par combinaison linéaire de fonctions d'onde de l'atome d'hydrogène.

La méthode C. L. O. A Cette méthode consiste à considérer que la fonction d'onde moléculaire est une Combinaison Linéaire des Orbitales Atomiques. HA Orbitale Atomique 1 s. A ==> f. A HB Orbitale Atomique 1 s. B ==> f. B HA __ HB Orbitale Moléculaire AB = a f. A + b f. B

On aura donc deux solutions pour AB : AB = a A + a B = a ( A + B) Si b = +a AB = a A - a B = a ( A - B) Si b = -a Ces deux expressions seront simultanément solutions de l'équation de Schrödinger. On obtient donc deux orbitales moléculaires à partir des deux orbitales atomiques.

• Y 1 décrit l'état moléculaire dit liant car il existe une zone d'espace qui peut être occupée par l'électron où il peut être en interaction indifféremment avec les noyaux PA ou P B. • Y 2 décrit l'état moléculaire dit antiliant car l'électron, dans une zone donnée de l'espace (lobe), ne peut être en interaction qu'avec le noyau voisin. Ces deux lobes sont séparés par la surface nodale, lieu des points où la probabilité de présence est nulle. Les deux noyaux restent ainsi distants de R 1 supérieure à la valeur d'équilibre R 0 vérifiant ainsi la définition de liaison chimique. On peut dire ainsi que Y 2 décrit toujours un état moléculaire excité caractérisé par une surface nodale entre les deux noyaux.

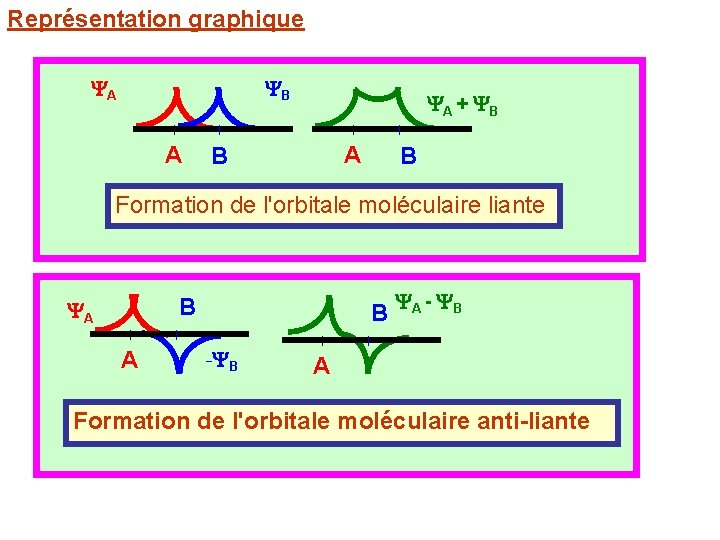
Représentation graphique A B A A + B A B B Formation de l'orbitale moléculaire liante B A A B - B A - B A Formation de l'orbitale moléculaire anti-liante

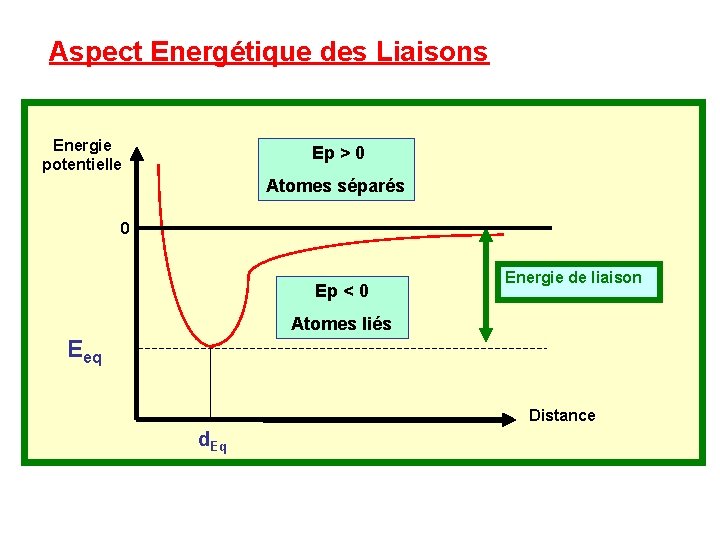
Aspect Energétique des Liaisons Energie potentielle Ep > 0 Atomes séparés 0 Ep < 0 Energie de liaison Atomes liés Eeq Distance d. Eq

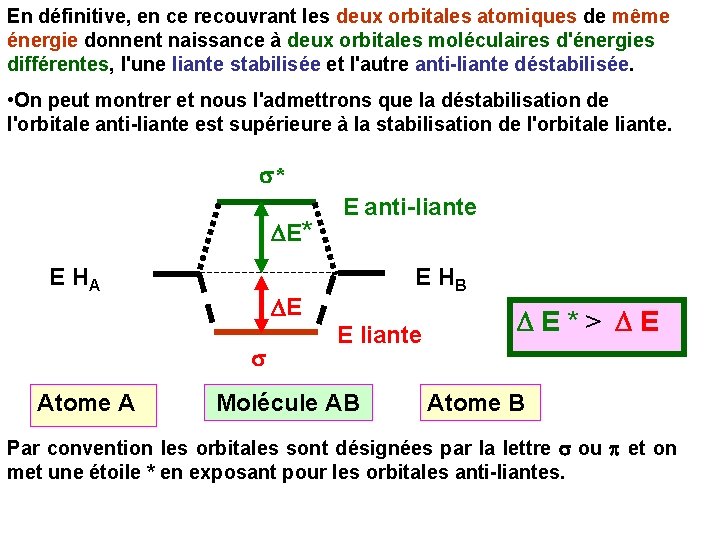
En définitive, en ce recouvrant les deux orbitales atomiques de même énergie donnent naissance à deux orbitales moléculaires d'énergies différentes, l'une liante stabilisée et l'autre anti-liante déstabilisée. • On peut montrer et nous l'admettrons que la déstabilisation de l'orbitale anti-liante est supérieure à la stabilisation de l'orbitale liante. s* DE* E HA E HB DE s Atome A E anti-liante E liante Molécule AB D E * > D E Atome B Par convention les orbitales sont désignées par la lettre s ou p et on met une étoile * en exposant pour les orbitales anti-liantes.

LA STRUCTURE MOLÉCULAIRE On peut avoir une idée sur la géométrie d'une molécule en appliquant la théorie VSEPR (Valence Shell Electron Pair Repulsion) de Gillespie basée sur la répulsion entre les "paires" d'électron présents dans la couche de valence de l'atome central. Le mot "paire" d'électrons englobe les électrons d'une liaison chimique (quelle soit simple, double ou triple) ou ceux d'un doublet libre. On notera: * L le nombre de liguants X autour de l'atome central A * D le nombre de doublets libres E de l'atome central A On obtient ainsi une disposition spatiale des "paires" électroniques et une géométrie définie par la disposition des liguants uniquement. La structure indiquée est en fait une structure idéalisée et la vraie structure sera légèrement différente et dépendra de chaque substituant.

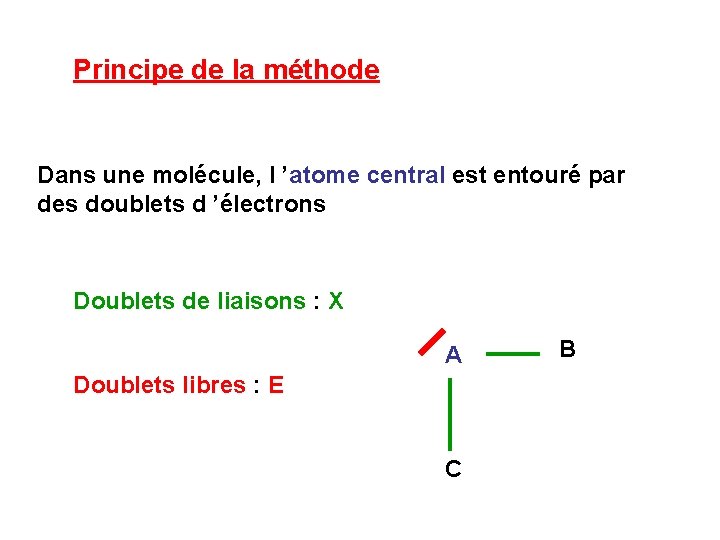
Principe de la méthode Dans une molécule, l ’atome central est entouré par des doublets d ’électrons Doublets de liaisons : X A Doublets libres : E C B

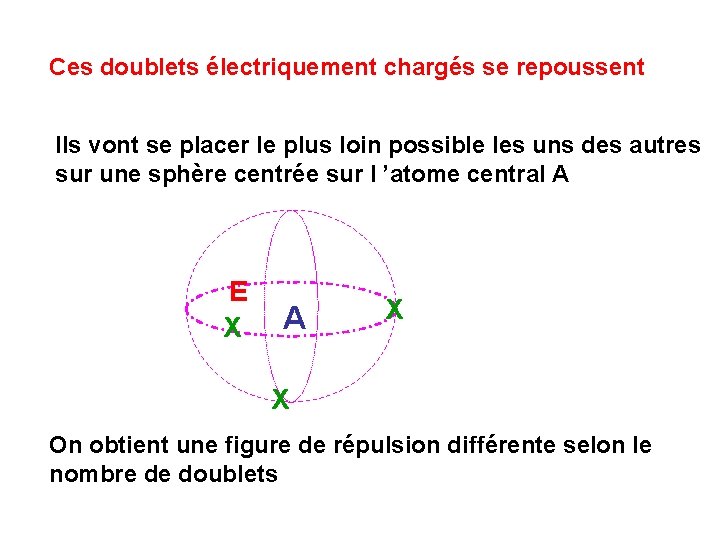
Ces doublets électriquement chargés se repoussent Ils vont se placer le plus loin possible les uns des autres sur une sphère centrée sur l ’atome central A E X A X X On obtient une figure de répulsion différente selon le nombre de doublets

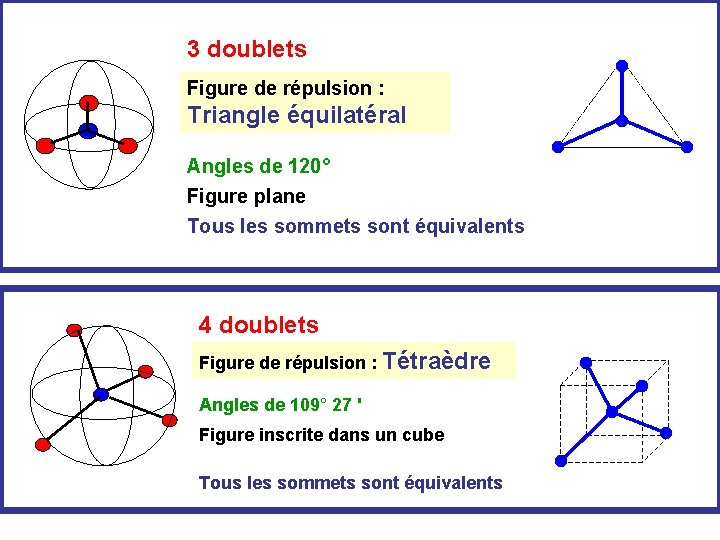
3 doublets Figure de répulsion : Triangle équilatéral Angles de 120° Figure plane Tous les sommets sont équivalents 4 doublets Figure de répulsion : Tétraèdre Angles de 109° 27 ' Figure inscrite dans un cube Tous les sommets sont équivalents

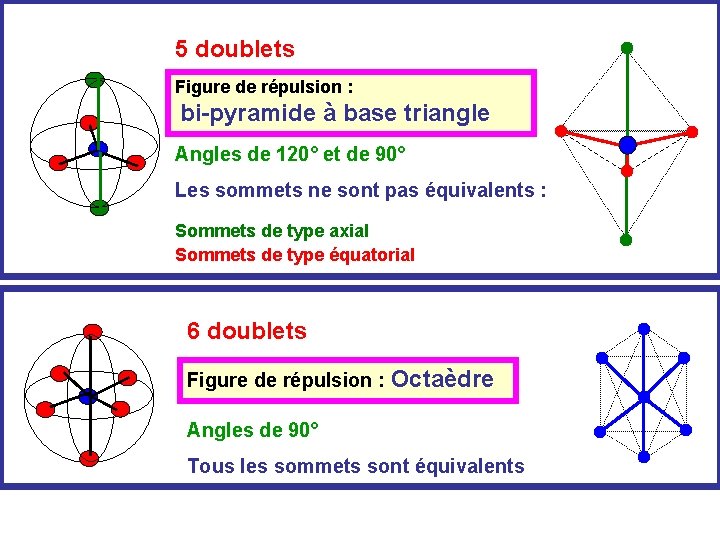
5 doublets Figure de répulsion : bi-pyramide à base triangle Angles de 120° et de 90° Les sommets ne sont pas équivalents : Sommets de type axial Sommets de type équatorial 6 doublets Figure de répulsion : Octaèdre Angles de 90° Tous les sommets sont équivalents

Détermination du type moléculaire AXn. Em Atome central n : nombre d ’atomes liés à l ’atome central m : nombre de doublets libres de l ’atome central

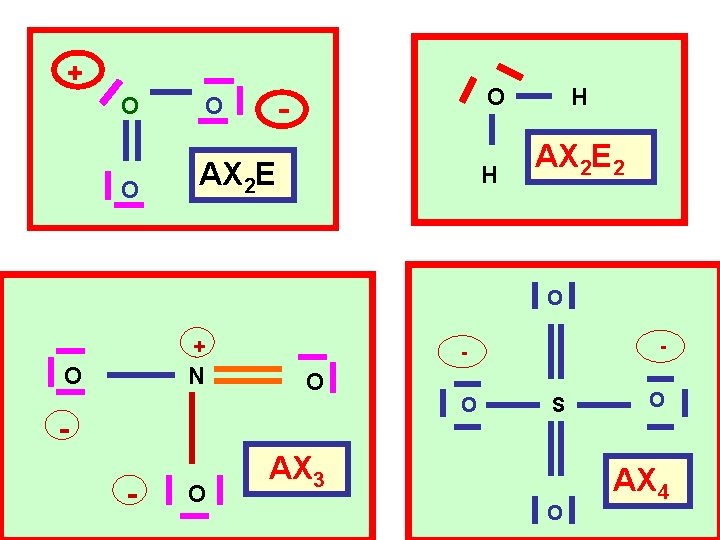
+ O O - O AX 2 E O H H AX 2 E 2 O + N O O - O S AX 3 O O AX 4

REMARQUES -Dans la méthode V. S. E. P. R la géométrie est déterminée uniquement par la répulsion entre les doublets de l'atome central. Les doublets libres des atomes latéraux n'entrent donc pas en ligne de compte. -Les liaisons multiples n'interviennent pas dans la détermination du type moléculaire. Elles sont considérées comme des liaisons simples. Ce n'est donc pas le nombre total de doublets de liaisons qui compte mais le nombre d'atomes liés à l'atome central.

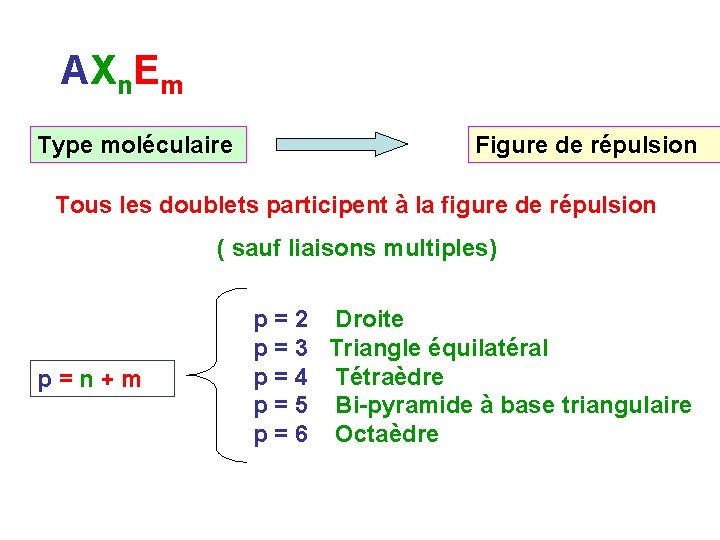
AXn. Em Type moléculaire Figure de répulsion Tous les doublets participent à la figure de répulsion ( sauf liaisons multiples) p = n + m p = 2 Droite p = 3 Triangle équilatéral p = 4 Tétraèdre p = 5 Bi-pyramide à base triangulaire p = 6 Octaèdre

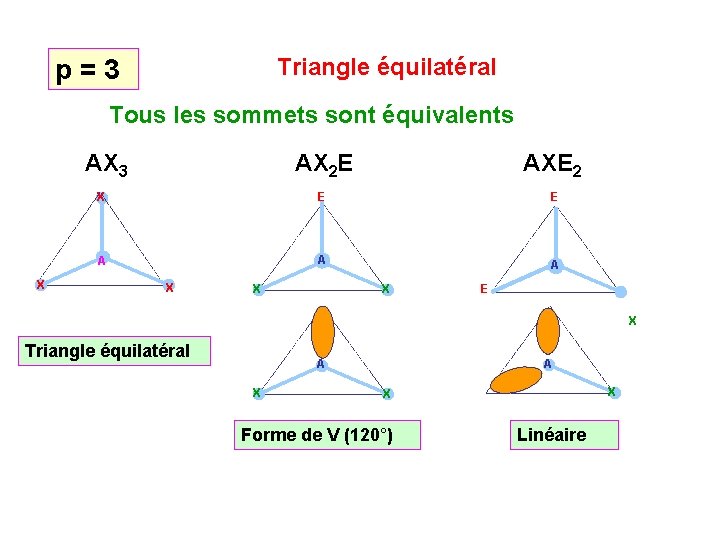
Triangle équilatéral p = 3 Tous les sommets sont équivalents AX 3 AXE 2 X E E A A A X X AX 2 E X X E X Triangle équilatéral A A X X X Forme de V (120°) Linéaire

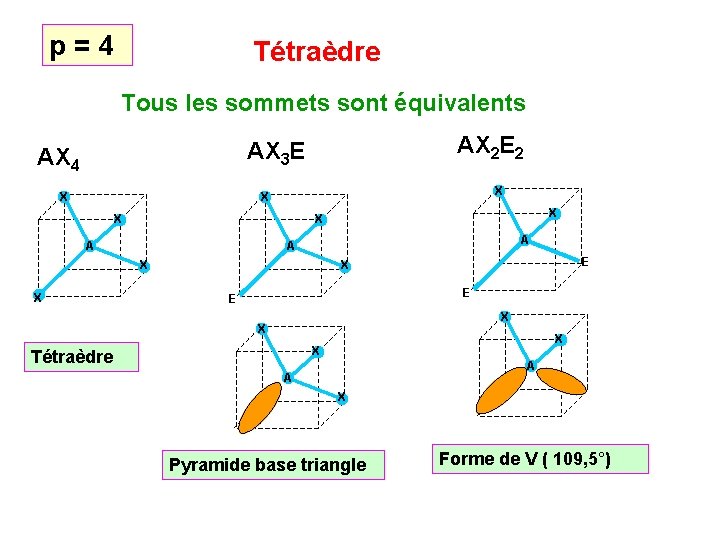
p = 4 Tétraèdre Tous les sommets sont équivalents AX 2 E 2 AX 3 E AX 4 X X A A A X X E X E E X X Tétraèdre A A X Pyramide base triangle Forme de V ( 109, 5°)

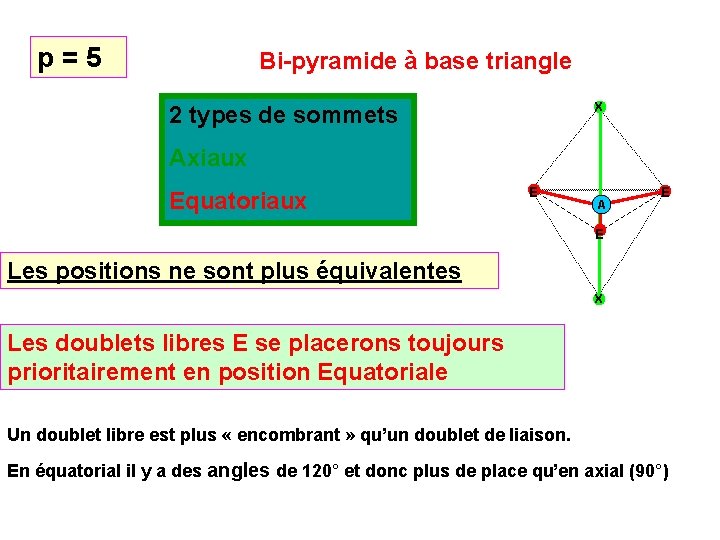
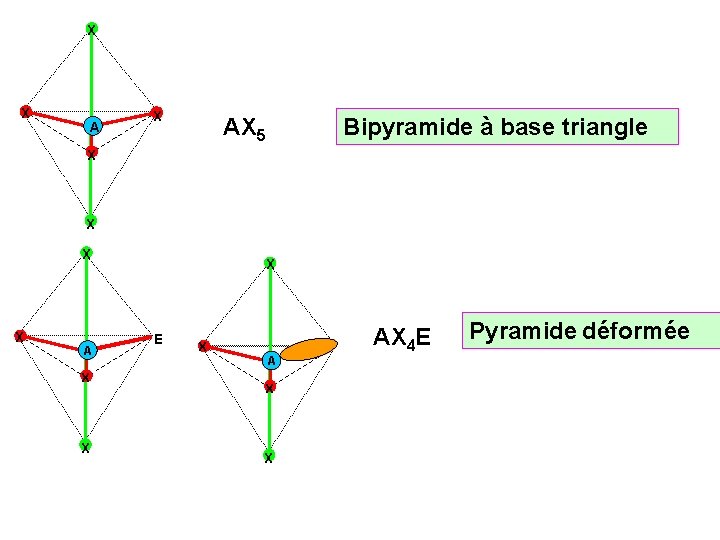
p = 5 Bi-pyramide à base triangle X 2 types de sommets Axiaux Equatoriaux E A E E Les positions ne sont plus équivalentes X Les doublets libres E se placerons toujours prioritairement en position Equatoriale Un doublet libre est plus « encombrant » qu’un doublet de liaison. En équatorial il y a des angles de 120° et donc plus de place qu’en axial (90°)

X X AX 5 Bipyramide à base triangle X X A X X X E X A X X AX 4 E Pyramide déformée

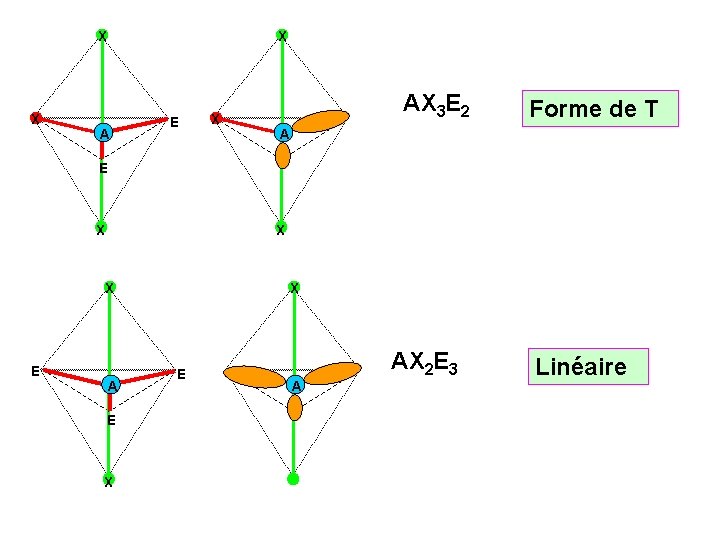
X X X A E X AX 3 E 2 Forme de T A E X X X E A E X X E A AX 2 E 3 Linéaire

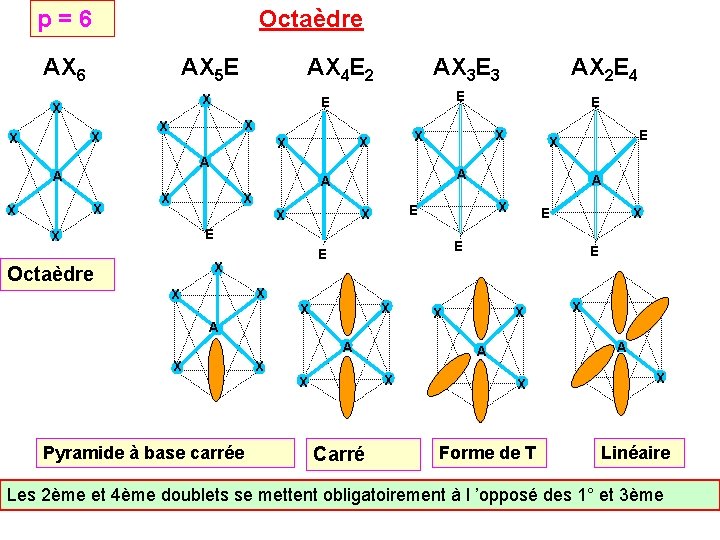
p = 6 Octaèdre AX 6 AX 5 E X X X A X X X E X X A A X X Pyramide à base carrée E X E E X Octaèdre A E X X X E X A A X X E X X X A AX 2 E 4 E E X X AX 3 E 3 X X AX 4 E 2 Carré X X X A A X X E X Forme de T X Linéaire Les 2ème et 4ème doublets se mettent obligatoirement à l ’opposé des 1° et 3ème

Résumé

LIAISONS POLARISEES B A +d A -d B XA < XB Si l ’électronégativité des deux atomes est très différente la liaison va être polarisée. L ’atome le plus électronégatif va attirer le doublet de liaison vers lui. Des charges partielles vont apparaître. Un dipôle électrique a été créé

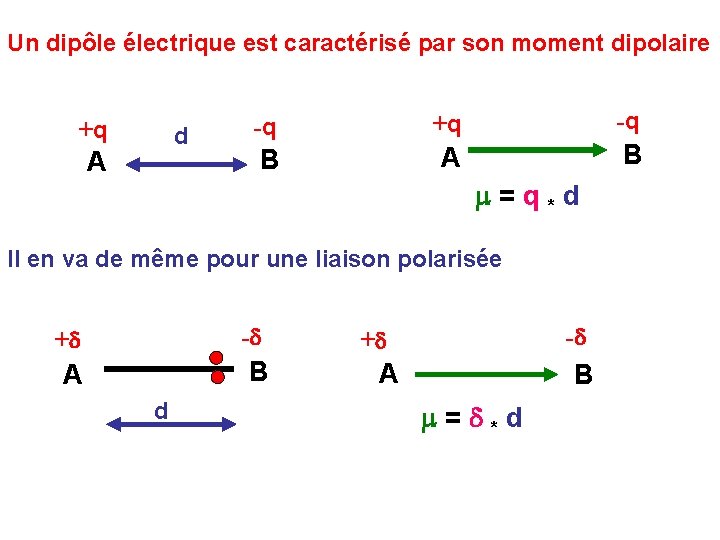
Un dipôle électrique est caractérisé par son moment dipolaire +q d A -q +q -q B A B m = q * d Il en va de même pour une liaison polarisée +d -d A B d -d +d A B m = d * d

Le moment dipolaire est une grandeur vectorielle Direction : celle de la liaison Sens : En chimie du pôle + vers le pôle Module ou intensité : m = d * d C. m m C +d m = d * d -d A B d En pratique on utilise unité mieux adaptée : Le Debye : 1 D = 3, 33 10 -30 C. m

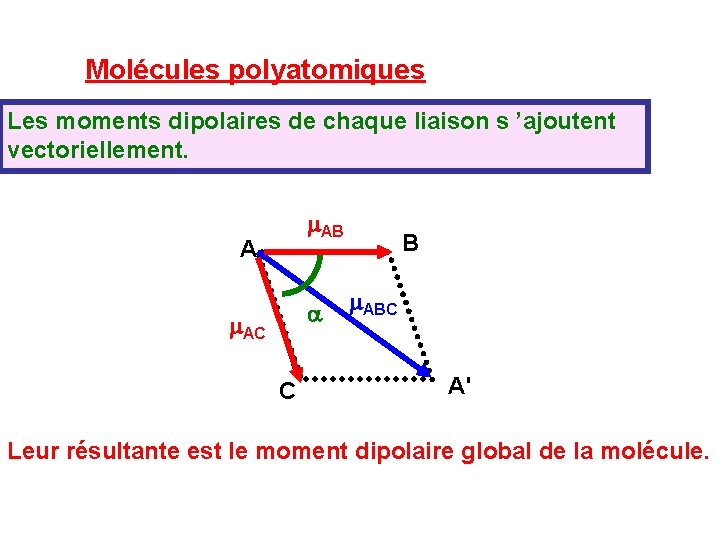
Molécules polyatomiques Les moments dipolaires de chaque liaison s ’ajoutent vectoriellement. m. AB A a m. AC C B m. ABC A' Leur résultante est le moment dipolaire global de la molécule.

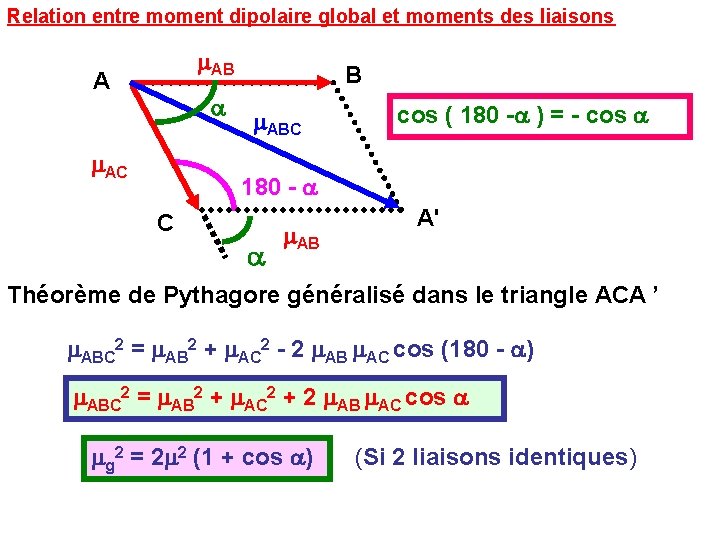
Relation entre moment dipolaire global et moments des liaisons m. AB A a m. AC B m. ABC cos ( 180 -a ) = - cos a 180 - a C a m. AB A' Théorème de Pythagore généralisé dans le triangle ACA ’ m. ABC 2 = m. AB 2 + m. AC 2 - 2 m. AB m. AC cos (180 - a) m. ABC 2 = m. AB 2 + m. AC 2 + 2 m. AB m. AC cos a mg 2 = 2 m 2 (1 + cos a) (Si 2 liaisons identiques)

Le moment dipolaire global d ’une molécule est une grandeur mesurable expérimentalement. Les moments de liaisons ne sont réellement mesurables que dans le cas de molécules diatomiques. Des tables ont été établies donnant les valeurs des moments dipolaires moyens de chaque type de liaison. On peut donc déterminer la valeur des moments dipolaires globaux à partir des valeurs des moments de liaisons données par ces tables. Cette méthode est assez approximative. D'une part, les moments dipolaires de liaisons donnés par les tables ne sont que des valeurs moyennes, d'autre part l'environnement influe sur leurs valeurs. Ainsi la présence de doublets libres modifie parfois sensiblement la valeur des moments dipolaires globaux.

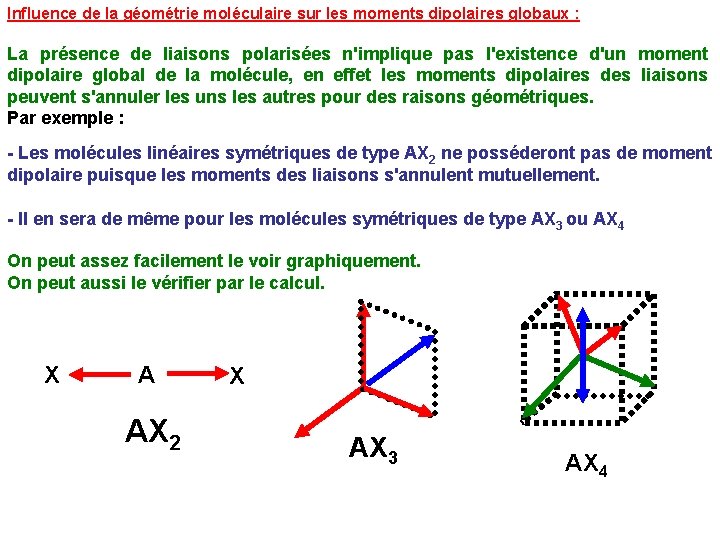
Influence de la géométrie moléculaire sur les moments dipolaires globaux : La présence de liaisons polarisées n'implique pas l'existence d'un moment dipolaire global de la molécule, en effet les moments dipolaires des liaisons peuvent s'annuler les uns les autres pour des raisons géométriques. Par exemple : - Les molécules linéaires symétriques de type AX 2 ne posséderont pas de moment dipolaire puisque les moments des liaisons s'annulent mutuellement. - Il en sera de même pour les molécules symétriques de type AX 3 ou AX 4 On peut assez facilement le voir graphiquement. On peut aussi le vérifier par le calcul. X A AX 2 X AX 3 AX 4

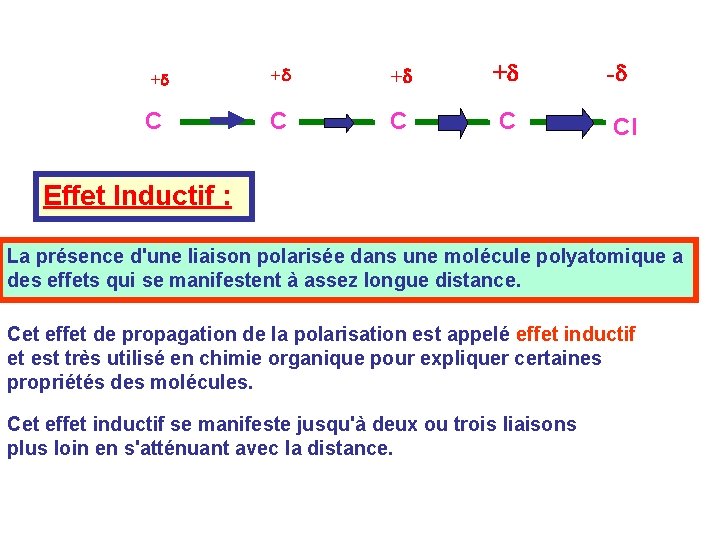
+d C +d +d +d -d C Cl Effet Inductif : La présence d'une liaison polarisée dans une molécule polyatomique a des effets qui se manifestent à assez longue distance. Cet effet de propagation de la polarisation est appelé effet inductif et est très utilisé en chimie organique pour expliquer certaines propriétés des molécules. Cet effet inductif se manifeste jusqu'à deux ou trois liaisons plus loin en s'atténuant avec la distance.

IONICITE DES LIAISONS On exprime l'ionicité d'une liaison par son pourcentage d'ionicité. Sa détermination nécessite la connaissance du moment dipolaire de liaison et de la longueur de celle-ci. m = d * d soit d = m / d +d A m = d * d d -d B Si d = 0 la liaison est purement covalente. Si d = e = 1, 6 10 -19 C la liaison est purement ionique. Le rapport d /e mesure directement le pourcentage d'ionicité de la liaison, par exemple si d / e = 0, 5 on dira que la liaison est ionique à 50 %.

%IAB = 100 * d / e = 100 m / de %IAB = 100 * m (C. m ) / d ( m ) / e ( C ) ou avec les unités courantes : %IAB = 20, 8 * m (D) / d ( Å ) Ce pourcentage d’ionicité est fortement corrélé avec la différence d ’électronégativité des deux atomes.