CHAPITRE II SPECTROSCOPIE DE ROTATION PURE I INTRODUCTION

CHAPITRE II SPECTROSCOPIE DE ROTATION PURE

I – INTRODUCTION Une molécule peut absorber ou émettre une radiation en acquérant un mouvement de rotation autour de son centre de gravité. Cela provoque des transitions entre niveaux d’énergie de rotation de la molécule.

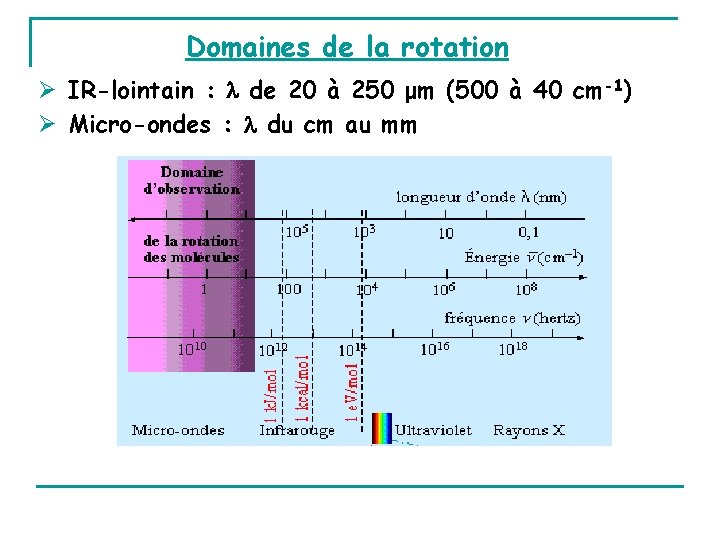
Domaines de la rotation IR-lointain : de 20 à 250 μm (500 à 40 cm-1) Micro-ondes : du cm au mm

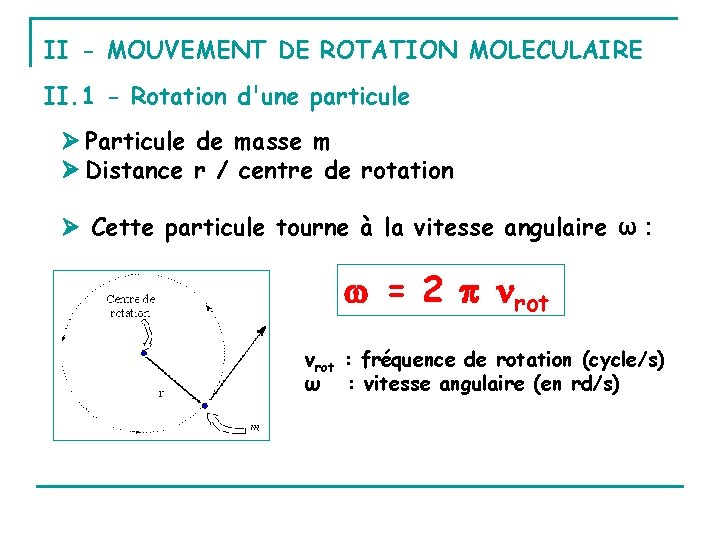
II - MOUVEMENT DE ROTATION MOLECULAIRE II. 1 - Rotation d'une particule Particule de masse m Distance r / centre de rotation Cette particule tourne à la vitesse angulaire ω : = 2 rot νrot : fréquence de rotation (cycle/s) ω : vitesse angulaire (en rd/s)

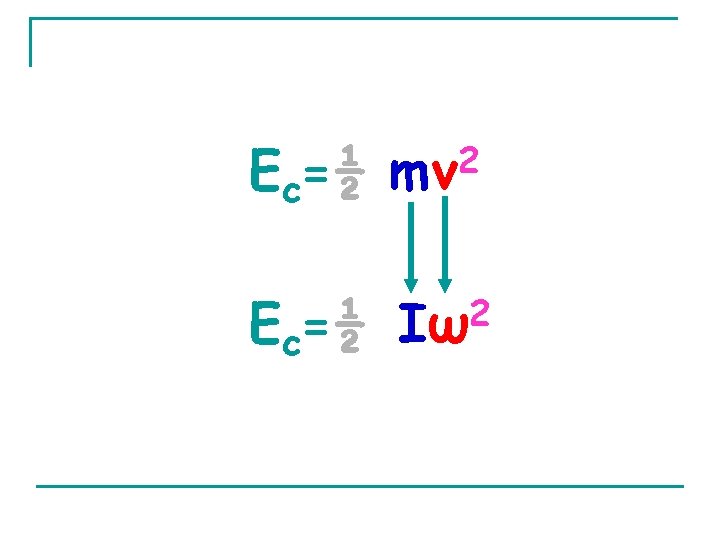
Energie cinétique En fonction de m et v (vitesse): Ec = ½ mv 2 En fonction de r et ω : Comme v = r ω Ec = ½ m(rω)2 = ½ (mr 2)ω2 I = mr 2 ; I étant le moment d'inertie Ec = ½ Iω 2

Ec=½ 2 mv Ec=½ 2 Iω

II. 2 - Rotation de la molécule diatomique – Cas du rotateur rigide Modèle mécanique simple : molécule diatomique supposée rigide ≡ deux sphères : rotateur rigide Modèle mécanique du rotateur rigide - Deux atomes de masses m 1 et m 2 - Chacun réduit à un point matériel

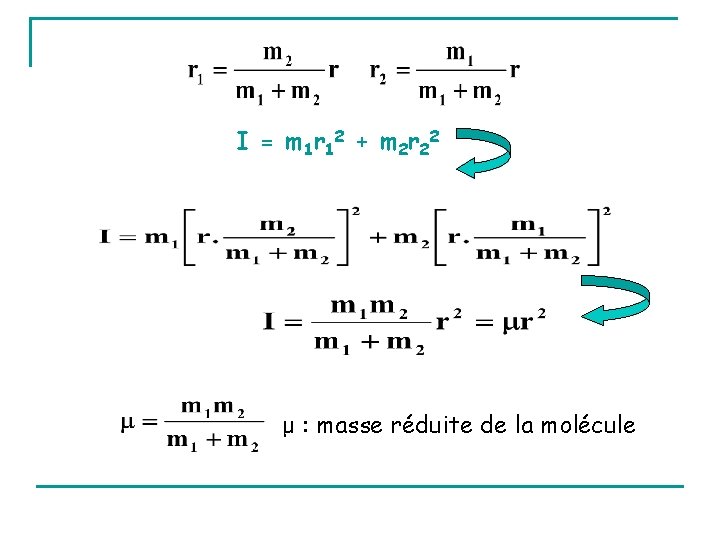
II. 2. 1 - Expression du moment d’inertie Cas général Cas de deux particules I = m 1 r 12 + m 2 r 22

I = f(r) r : distance internucléaire = longueur de liaison de la molécule diatomique I = m 1 r 12 + m 2 r 22 r = r 1+r 2 r 1 = r-r 2 et r 2 = r-r 1 D’autre part Position du centre de gravité d’une molécule diatomique : m 1 r 1 = m 2 r 2 m 1 r 1 = m 2 (r-r 1) et m 2 r 2 = m 1 (r-r 2) m 1 r 1+m 2 r 1 = m 2 r et m 2 r 2+m 1 r 2 = m 1 r

I = m 1 r 12 + m 2 r 22 μ : masse réduite de la molécule

Equivalent mécanique du rotateur diatomique rigide Comme I = μr 2 Molécule diatomique ≡ Atome unique : - de masse μ - tournant autour d’un point - situé à la distance fixe r = la distance internucléaire

II. 2. 2 - Expression de l’énergie cinétique E c = ½ m 1 v 12 + ½ m 2 v 22 v 1 = r 1ω v 2 = r 2ω Ec = ½ ω2 (m 1 r 12 + m 2 r 22) or, I = m 1 r 12 + m 2 r 22 Ec = ½ I ω 2 Analogie quantité de mouvement p = m v moment cinétique P = I ω En résumé Ec = ½ Iω 2 I = μ r 2 μ = m 1 m 2/(m 1+m 2) P = Iω

III - ENERGIE DE ROTATION Système microscopique Solution du problème des énergies : Résolution de l'équation de Schrödinger Introduction de nombres quantiques Quantification de l'énergie

Cas d'un mouvement de rotation Quantification de l'énergie : Restrictions quantiques sont fonction du moment cinétique Valeurs permises du moment cinétique : Multiples de Valeur propre de l’opérateur moment cinétique : J = 0, 1, 2. . . : entier, nombre quantique de rotation

Expression de l’énergie cinétique de rotation Ec = ½ Iω 2 = (Iω)2/2 I J = 0, 1, 2. .

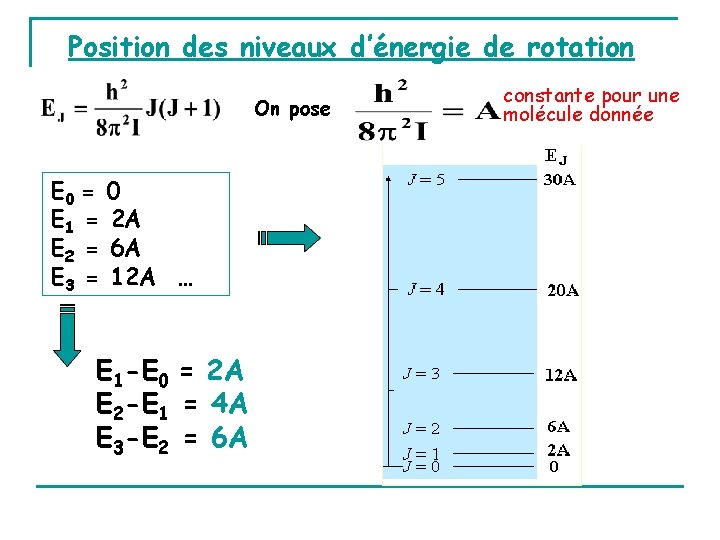
Position des niveaux d’énergie de rotation On pose E 0 = 0 E 1 = 2 A E 2 = 6 A E 3 = 12 A … E 1 -E 0 = 2 A E 2 -E 1 = 4 A E 3 -E 2 = 6 A constante pour une molécule donnée

IV - SPECTRE DE ROTATION IV. 1 - Règles de sélection Moment de transition relié au moment dipolaire Moment dipolaire électrique nul (molécules diatomiques homonucléaires H 2, N 2, O 2) Pas de transitions de rotation Molécules hétéronucléaires : * Niveaux d’énergie fonction de J * Intervention de règles de sélection ΔJ = ± 1

Transitions permises ΔJ = ± 1 n n entre un niveau J et un niveau J+1 en absorption entre un niveau J et un niveau J-1 en émission Cas de l’absorption

IV. 2 - Positions des raies de rotation Absorption : Transition entre 2 niveaux J et J+1 une raie sur le spectre 1ère raie : Transition J → (J+1) noté constante pour une molécule donnée constante de rotation Raie suivante : transition (J+1) → (J+2)

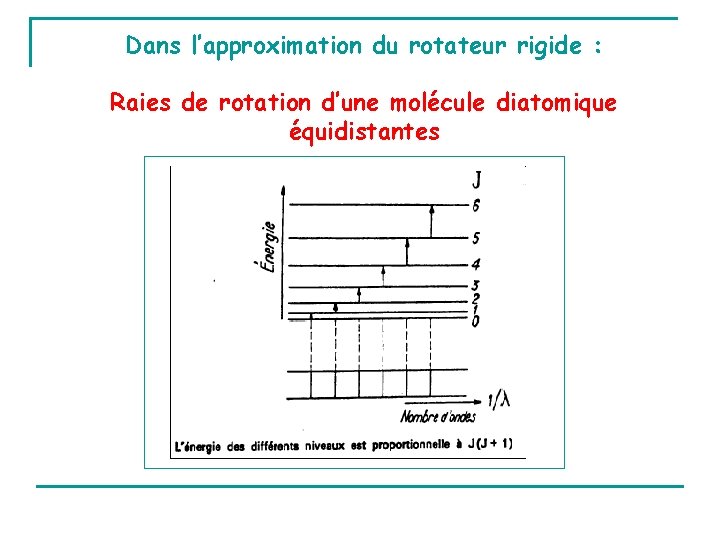
Intervalle entre deux raies consécutives 2 B = constante raies équidistantes

Dans l’approximation du rotateur rigide : Raies de rotation d’une molécule diatomique équidistantes

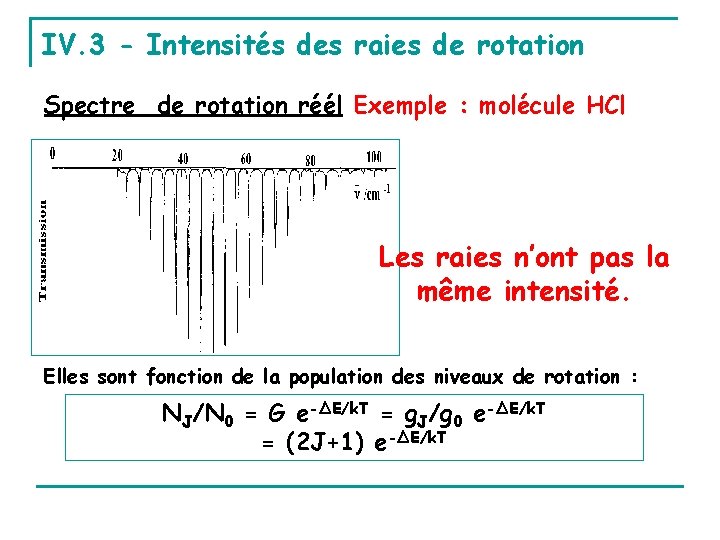
IV. 3 - Intensités des raies de rotation Spectre de rotation réél Exemple : molécule HCl Les raies n’ont pas la même intensité. Elles sont fonction de la population des niveaux de rotation : NJ/N 0 = G e-ΔE/k. T = g. J/g 0 e-ΔE/k. T = (2 J+1) e-ΔE/k. T

V - LA ROTATION DES MOLÉCULES POLYATOMIQUES V. 1 - Molécules polyatomiques linéaires Expression de l’énergie de rotation Molécule polyatomique linéaire ≡ Molécule diatomique J = 0, 1, 2. . I : moment d’inertie du système (valeur unique)

Niveaux d’énergie Pour une molécule linéaire polyatomique, les raies sont équidistantes MAIS elles sont plus rapprochées que pour les molécules diatomiques CAR le moment d’inertie est plus grand. Exemple H-12 C≡ 14 N : B = 1, 48 cm-1 H-35 Cl : B = 20, 68 cm-1

Règle de sélection ΔJ = ± 1 Pas de spectre de rotation pure pour les molécules symétriques (CO 2, C 2 H 2) ≡ molécules diatomiques homonucléaires (O 2, N 2…) DIFFERENCE : Molécule diatomique : une seule valeur de r Molécule polyatomique : au moins deux distances internucléaires (n – 1) liaisons pour une molécule contenant n atomes

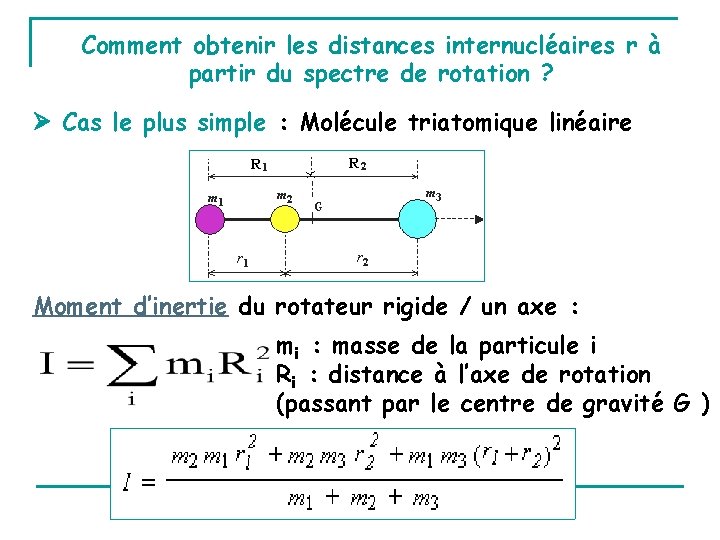
Comment obtenir les distances internucléaires r à partir du spectre de rotation ? Cas le plus simple : Molécule triatomique linéaire Moment d’inertie du rotateur rigide / un axe : mi : masse de la particule i Ri : distance à l’axe de rotation (passant par le centre de gravité G )

Résolution mathématique du problème En considérant des molécules isotopiques * Deux liaisons Deux molécules isotopiquement différentes Exemple : 16 O=12 C=32 S et 16 O=12 C=34 S * r ne varie pratiquement pas avec la substitution isotopique MAIS I varie. Problème ramené à la résolution de 2 équations en I à 2 inconnues (r 1 et r 2) valeurs de I : prises expérimentalement

V. 2 - Molécules polyatomiques non linéaires ou spatiales 3 moments d'inertie IA, IB et IC selon 3 axes perpendiculaires appelés axes principaux : Trois catégories de molécules IA = IB = IC IA ≠ IB = IC IA ≠ IB ≠ IC

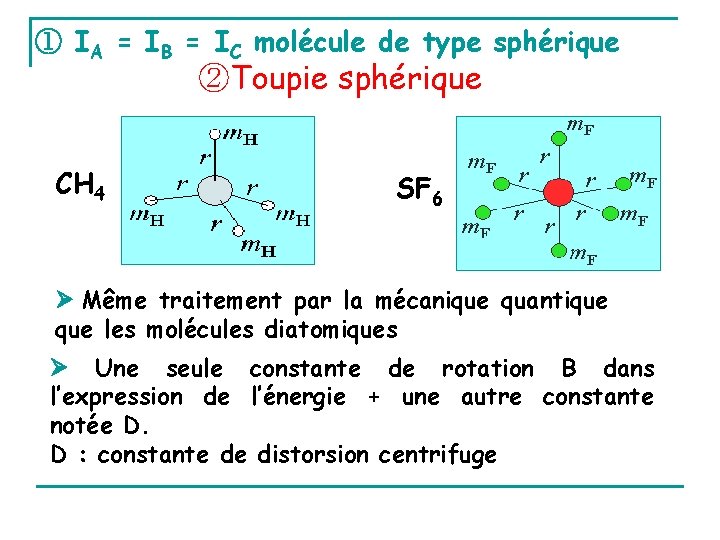
① IA = IB = IC molécule de type sphérique ②Toupie sphérique CH 4 SF 6 Même traitement par la mécanique quantique les molécules diatomiques Une seule constante de rotation B dans l’expression de l’énergie + une autre constante notée D. D : constante de distorsion centrifuge

② IA ≠ IB = IC Toupie symétrique Deux moments d’inertie égaux CH 3 Cl Br. F 5 PCl 5 2 moments d’inertie distincts dans l’équation de Schrödinger : Définition de 2 nombres quantiques J + nouveau nombre quantique K K = J, J-1, J-2, …, 0, …, -(J-1), -J Règles de sélection: ΔJ = ± 1 ; ΔK= 0

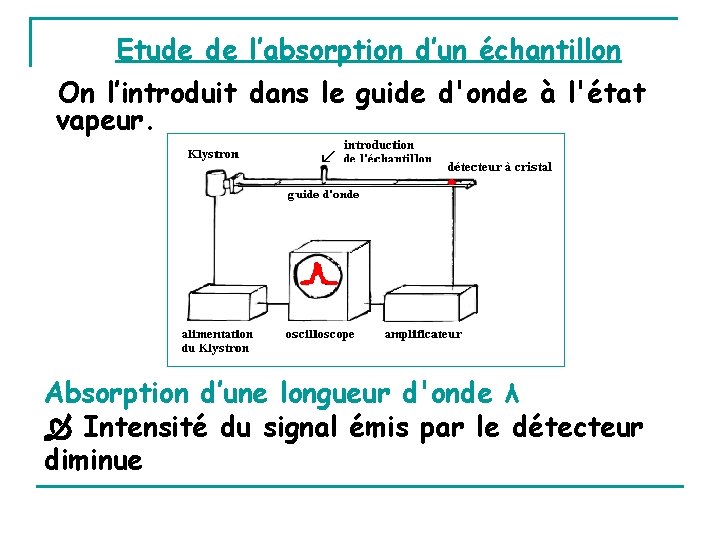
VI - APPAREILLAGE Source : dispositif électronique appelé Klystron Onde canalisée le long tube rectangulaire Guide d’onde Electrons accélérés dans cavité du tube (Klystron) par ddp convenable La cavité entre en résonance production d’une onde monochromatique dans la région micro-ondes Variation ddp du Klystron Balayage d’un domaine de micro-ondes Onde détecteur : cristal de quartz entrant en vibration sous l'action de la radiation Vibrations du cristal de quartz produisent un signal électrique amplifié enregistré sur un oscilloscope

Etude de l’absorption d’un échantillon On l’introduit dans le guide d'onde à l'état vapeur. Absorption d’une longueur d'onde λ Intensité du signal émis par le détecteur diminue

VII - APPLICATIONS Spectroscopie de rotation non utilisée en routine dans les laboratoires de Chimie Limitée en pratique aux petites molécules Elle permet des mesures très précises des moments d’inertie : renseignements sur la dimension des molécules Un de ses domaines d’applications les plus importants : astrochimie ( identification de nombreuses molécules dans les espaces interstellaires)