Chapitre FRACTIONS 10 FR I DECIMAL et FRACTION

Chapitre FRACTIONS 10 -FR I - DECIMAL et FRACTION II – QUOTIENTS EGAUX III- ADDITION / SOUSTRACTION IV – MULTIPLICATION V - INVERSE / DIVISION VI - CALCULS Bernard 4° Avon

I-DECIMAL ET FRACTION Ex 1: = 5 ÷ 8 = 0, 625 = 6 ÷ (-2) = -3 Les divisions se terminent. L’écriture décimale est exacte Les quotients et sont des décimaux = 15 ÷ 7 2, 142857143… La division ne se termine pas. L’écriture décimale est approchée Ex 1: Le quotient n’est pas un décimal Il est donc nécessaire d’écrire ce nombre sous forme d’un quotient ou fraction pour avoir la valeur exacte

II-FRACTIONS EQUIVALENTES 1) Définition Nous dirons que 2 fractions sont équivalentes (ou égales) si elles représente le même quotient Ex: 1, 5 2) Produit en croix On remarque 2 x 18 = 36 3 x 12 =36 2 fractions sont égales si les produits en croix sont égaux

alors Si Démonstration posons axd=bxc Dividende = diviseur x quotient D’après la définition du quotient a = bq ‘’’’’ c = dq’ et axd a x d = bq x d a x d = bd x q ‘’’’’’ Comparons et bxc b x c = b x dq’ b x c = bd x q’ Les 2 quotients étant égaux q = q’ a x d = bd x q b x c = bd x q Donc a x d = b x c C. Q. F. D

Réciproquement : Si axd=bxc Avec alors a, b, c et d (b ≠ 0 et d ≠ 0)

3) Simplification des fractions Le quotient de deux nombres en écriture fractionnaire ne change pas si l’on multiplie ( ou si l’on divise) par un même nombre non nul le numérateur et le dénominateur. avec k ≠ 0 Remarque : Cette règle sert à simplifier des fractions ou à les « réduire » au même dénominateur. Ex: Dans cet exemple on a simplifié par 5 puis par 3

III-ADDITION DES FRACTIONS 1) Fractions de même dénominateur Pour additionner ou soustraire deux fractions de même dénominateur: On additionne ou on soustrait les numérateurs On garde le dénominateur commun et Ex:

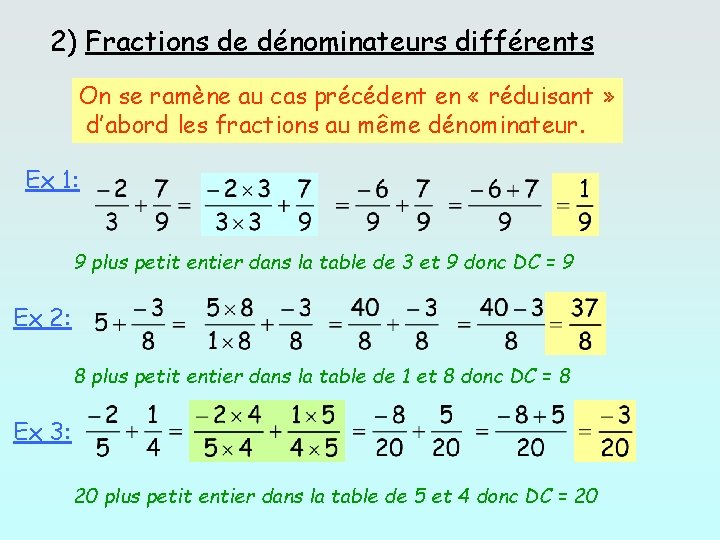
2) Fractions de dénominateurs différents On se ramène au cas précédent en « réduisant » d’abord les fractions au même dénominateur. Ex 1: 9 plus petit entier dans la table de 3 et 9 donc DC = 9 Ex 2: 8 plus petit entier dans la table de 1 et 8 donc DC = 8 Ex 3: 20 plus petit entier dans la table de 5 et 4 donc DC = 20

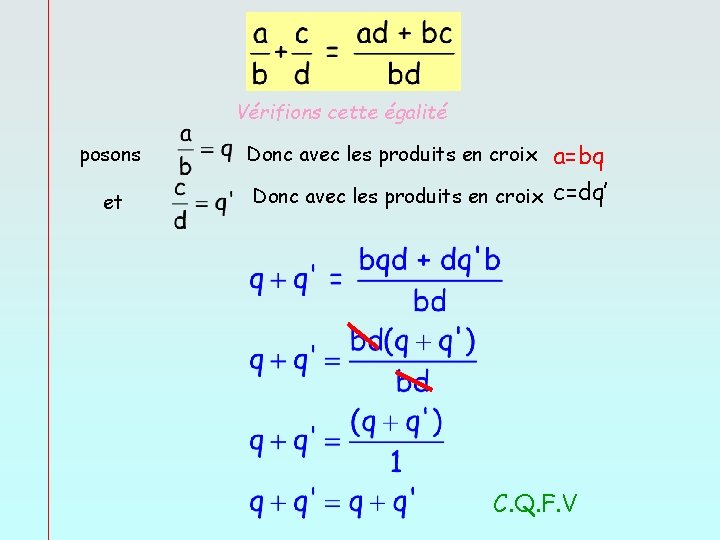
Vérifions cette égalité posons et a=bq Donc avec les produits en croix c=dq’ Donc avec les produits en croix C. Q. F. V

Récapitulatif de la procédure Etape 1 Trouver le dénominateur commun On le trouve en multipliant les deux dénominateurs ensemble (ou en prenant le plus petit commun multiple des deux).

Etape 2 Calculer les fractions équivalentes On multiplie le numérateur et le dénominateur par le même nombre.

Etape 3 Additionner les numérateurs entre eux On additionne les numérateurs entre eux (le dénominateur reste le même).

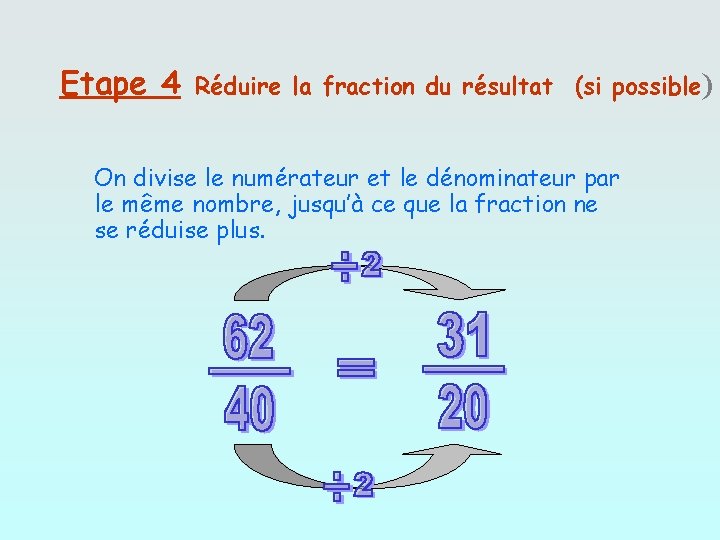
Etape 4 Réduire la fraction du résultat (si possible) On divise le numérateur et le dénominateur par le même nombre, jusqu’à ce que la fraction ne se réduise plus.

Tableau récapitulatif de la procédure Etape 1 Trouver le dénominateur commun Etape 2 Calculer les fractions équivalentes Etape 3 Additionner les numérateurs entre eux Etape 4 Réduire le résultat (si possible)

IV-MULTIPLICATION DES FRACTIONS Pour multiplier deux fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux. (avec b ≠ 0 et d ≠ 0) Ex 1: Ex 2: 3 est comme 3/1

V-DIVISION 1) Le nombre inverse Lorsque le produit de deux nombres est égal à 1, on dit qu’ils sont inverses l’un de l’autre. Ex: L’inverse de x est (avec x ≠ 0) L’inverse de (avec a ≠ 0 et b ≠ 0) est

2) La division Diviser = multiplier par l’ inverse. (avec b ≠ 0, c ≠ 0 et d ≠ 0) Donc, pour diviser par une fraction on multiplie par la fraction inversée Ex 1: On inverse Ex 2:

VI. EXEMPLES DE CALCULS Effectuer les calculs suivants en détaillant les étapes : Ex 1: Le dénominateur commun de 1 et 8 est 8 Le dénominateur commun de 7 et 42 est 42 On simplifie par 7

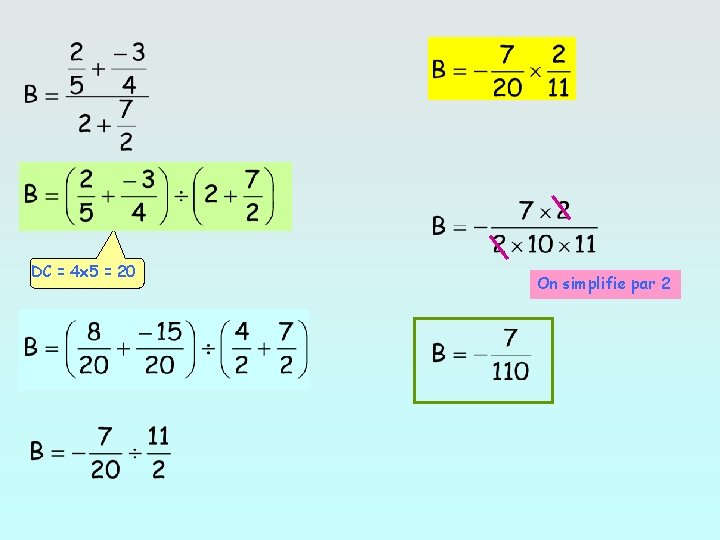
DC = 4 x 5 = 20 On simplifie par 2

FRACTIONS Revoir les exercices Apprendre le cours FIN