Chapitre 3 Les Matrices Description Une matrice est

Chapitre 3 Les Matrices

Description Une matrice est un tableau rectangulaire d’éléments (bidimensionnels). Les vecteurs sont des matrices avec une seule ligne ou une seule colonne (monodimensionnels). Pour insérer une matrice, il faut respecter les règles suivantes : • Les éléments doivent être mises entre des crochets [ et ] • Les espaces ou les virgules sont utilisés pour séparer les éléments dans la même ligne. • Un point-virgule (ou la touche entrer) est utilisé pour séparer les lignes.

Description Exemples : >> A = [1, 2, 3, 4 ; 5, 6, 7, 8 ; 9, 10, 11, 12] ; >> A = [1 2 3 4 ; 5 6 7 8 ; 9 10 11 12] ; >> A = [1, 2, 3, 4 5, 6, 7, 8 9, 10, 11, 12] ; >> A=[[1; 5; 9] , [2; 6; 10] , [3; 7; 11] , [4; 8; 12]] ;

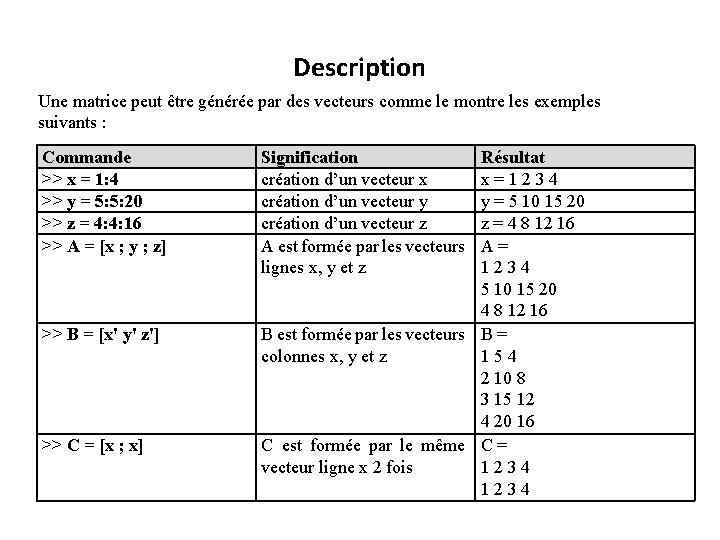
Description Une matrice peut être générée par des vecteurs comme le montre les exemples suivants : Commande >> x = 1: 4 >> y = 5: 5: 20 >> z = 4: 4: 16 >> A = [x ; y ; z] >> B = [x' y' z'] >> C = [x ; x] Signification création d’un vecteur x création d’un vecteur y création d’un vecteur z A est formée par les vecteurs lignes x, y et z Résultat x=1234 y = 5 10 15 20 z = 4 8 12 16 A= 1234 5 10 15 20 4 8 12 16 B est formée par les vecteurs B = colonnes x, y et z 154 2 10 8 3 15 12 4 20 16 C est formée par le même C = vecteur ligne x 2 fois 1234

Adressages et indexages Il est utile de noter les possibilités suivantes : • L’accès à un élément de la ligne i et la colonne j se fait par : A(i, j) • L’accès à toute la ligne numéro i se fait par : A(i, : ) • L’accès à toute la colonne numéro j se fait par : A(: , j)

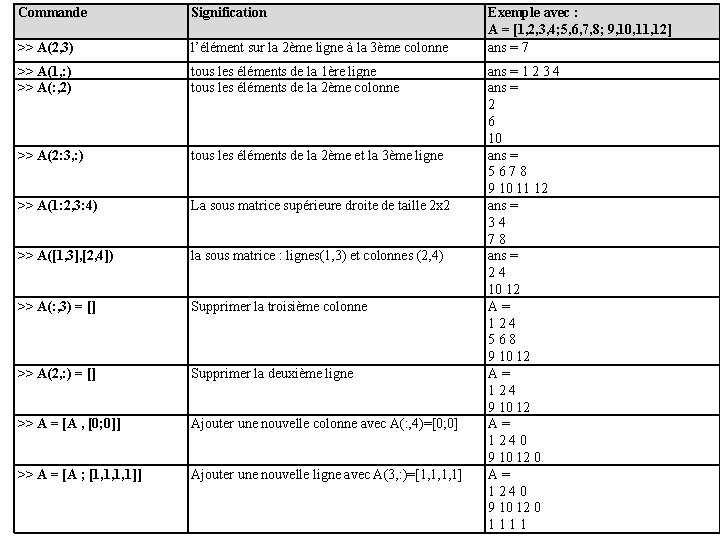
Commande Signification >> A(2, 3) l’élément sur la 2ème ligne à la 3ème colonne >> A(1, : ) >> A(: , 2) tous les éléments de la 1ère ligne tous les éléments de la 2ème colonne >> A(2: 3, : ) tous les éléments de la 2ème et la 3ème ligne >> A(1: 2, 3: 4) La sous matrice supérieure droite de taille 2 x 2 >> A([1, 3], [2, 4]) la sous matrice : lignes(1, 3) et colonnes (2, 4) >> A(: , 3) = [] Supprimer la troisième colonne >> A(2, : ) = [] Supprimer la deuxième ligne >> A = [A , [0; 0]] Ajouter une nouvelle colonne avec A(: , 4)=[0; 0] >> A = [A ; [1, 1, 1, 1]] Ajouter une nouvelle ligne avec A(3, : )=[1, 1, 1, 1] Exemple avec : A = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12] ans = 7 ans = 1 2 3 4 ans = 2 6 10 ans = 5678 9 10 11 12 ans = 34 78 ans = 24 10 12 A= 124 568 9 10 12 A= 1240 9 10 12 0 1111

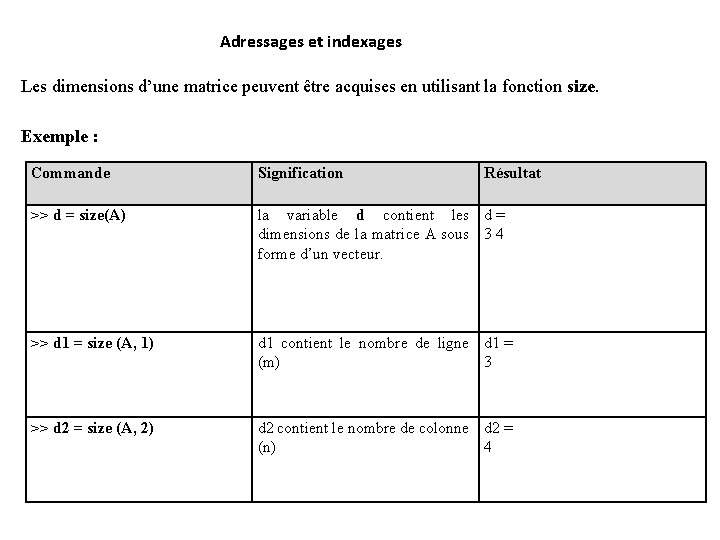
Adressages et indexages Les dimensions d’une matrice peuvent être acquises en utilisant la fonction size. Exemple : Commande Signification Résultat >> d = size(A) la variable d contient les d = dimensions de la matrice A sous 3 4 forme d’un vecteur. >> d 1 = size (A, 1) d 1 contient le nombre de ligne d 1 = (m) 3 >> d 2 = size (A, 2) d 2 contient le nombre de colonne d 2 = (n) 4

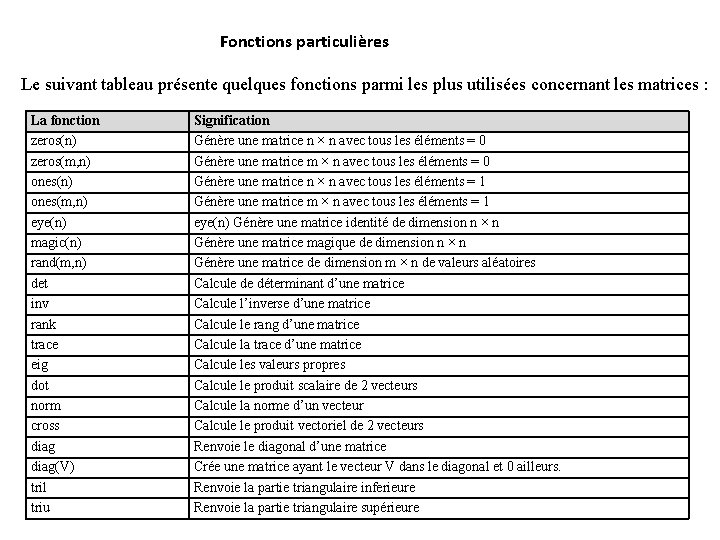
Fonctions particulières Le suivant tableau présente quelques fonctions parmi les plus utilisées concernant les matrices : La fonction zeros(n) zeros(m, n) ones(m, n) eye(n) magic(n) rand(m, n) det inv rank trace eig dot norm cross diag(V) tril triu Signification Génère une matrice n × n avec tous les éléments = 0 Génère une matrice m × n avec tous les éléments = 0 Génère une matrice n × n avec tous les éléments = 1 Génère une matrice m × n avec tous les éléments = 1 eye(n) Génère une matrice identité de dimension n × n Génère une matrice magique de dimension n × n Génère une matrice de dimension m × n de valeurs aléatoires Calcule de déterminant d’une matrice Calcule l’inverse d’une matrice Calcule le rang d’une matrice Calcule la trace d’une matrice Calcule les valeurs propres Calcule le produit scalaire de 2 vecteurs Calcule la norme d’un vecteur Calcule le produit vectoriel de 2 vecteurs Renvoie le diagonal d’une matrice Crée une matrice ayant le vecteur V dans le diagonal et 0 ailleurs. Renvoie la partie triangulaire inferieure Renvoie la partie triangulaire supérieure

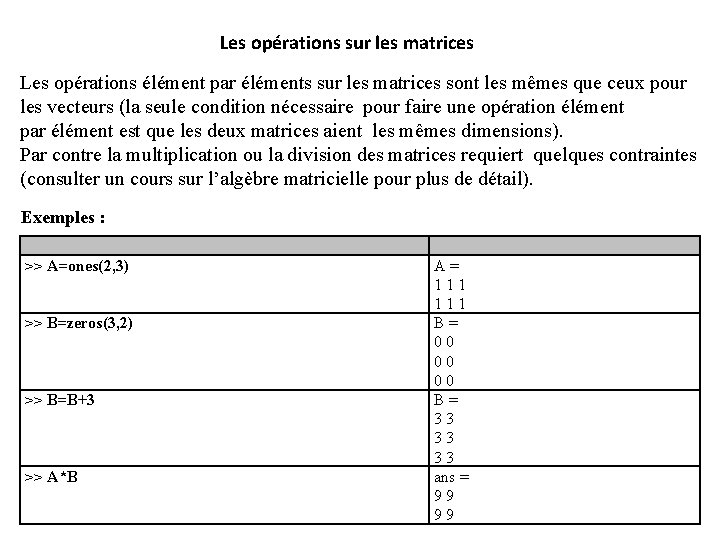
Les opérations sur les matrices Les opérations élément par éléments sur les matrices sont les mêmes que ceux pour les vecteurs (la seule condition nécessaire pour faire une opération élément par élément est que les deux matrices aient les mêmes dimensions). Par contre la multiplication ou la division des matrices requiert quelques contraintes (consulter un cours sur l’algèbre matricielle pour plus de détail). Exemples : >> A=ones(2, 3) >> B=zeros(3, 2) >> B=B+3 >> A*B A= 111 B= 00 00 00 B= 33 33 33 ans = 99 99

Les opérations sur les matrices Exemples : >> B=[B , [3 3 3]'] B= 333 333 >> B=B(1: 2, : ) B= 333 >> A=A*2 A= 222 >> A. *B ans = 666 >> A*eye(3) ans = 222

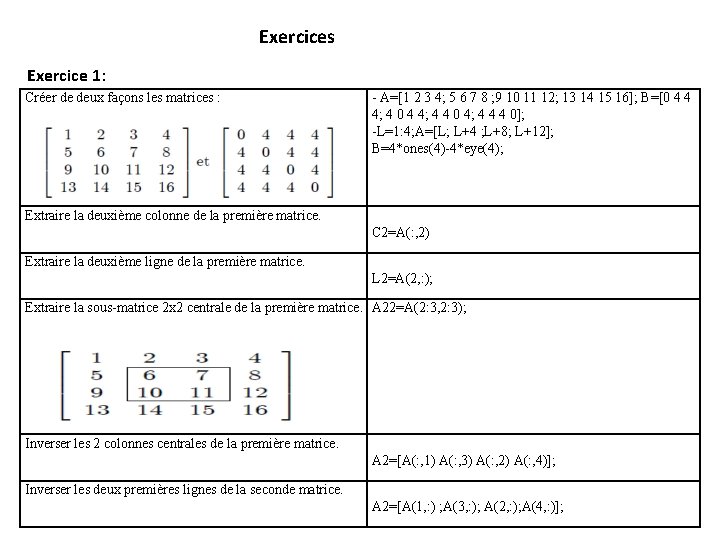
Exercices Exercice 1: Créer de deux façons les matrices : - A=[1 2 3 4; 5 6 7 8 ; 9 10 11 12; 13 14 15 16]; B=[0 4 4 4; 4 0 4 4; 4 4 0 4; 4 4 4 0]; -L=1: 4; A=[L; L+4 ; L+8; L+12]; B=4*ones(4)-4*eye(4); Extraire la deuxième colonne de la première matrice. C 2=A(: , 2) Extraire la deuxième ligne de la première matrice. L 2=A(2, : ); Extraire la sous-matrice 2 x 2 centrale de la première matrice. A 22=A(2: 3, 2: 3); Inverser les 2 colonnes centrales de la première matrice. A 2=[A(: , 1) A(: , 3) A(: , 2) A(: , 4)]; Inverser les deux premières lignes de la seconde matrice. A 2=[A(1, : ) ; A(3, : ); A(2, : ); A(4, : )];

Exercice 2: Questions Réponses Créez la matrice M définit par : M=[1 0 2 -4 ; 3 2 1 0 ; 0 4 7 6] ; Extraire la première ligne de M. M(1 ; : ) Extraire la troisième colonne de M. M( : ; 3) Extraire la sous-matrice de M définit par : M( 1 : 2 ; 2 : 4) ; Extraire la sous-matrice de M définit par : M 1(M(1 ; 1 : 3) ; M(3 ; 1 : 3)) ; Calculer le déterminant de M. Det(M) ; Calculer la matrice inverse de M Inv(M) ;

Exercice 3 : En utilisant uniquement les commandes « ones » et « zeros » donner les instructions qui permettent de construire les matrices A, B et C. A=[ones(3, 1), zeros(3, 1), ones(3, 1)] B=[ones(1, 3); zeros(2, 3)] C=[ones(3, 1), [zeros(2); ones(1, 2)]]