Chapitre 3 Les fonctions rationnelles MHF 4 U


























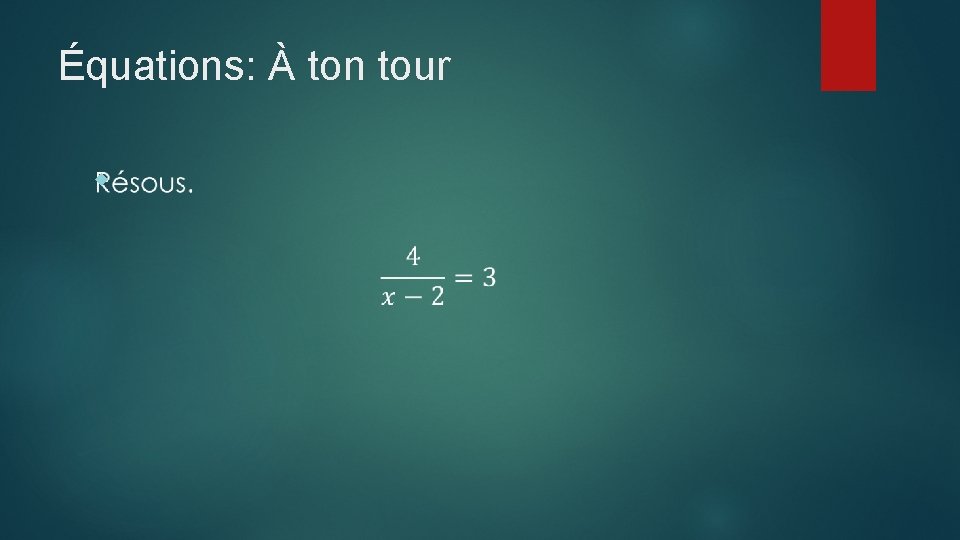

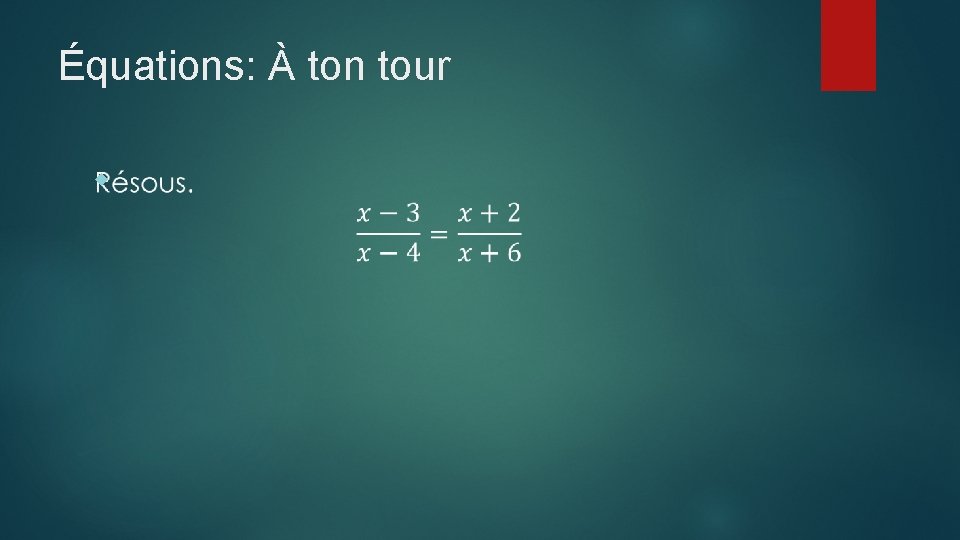


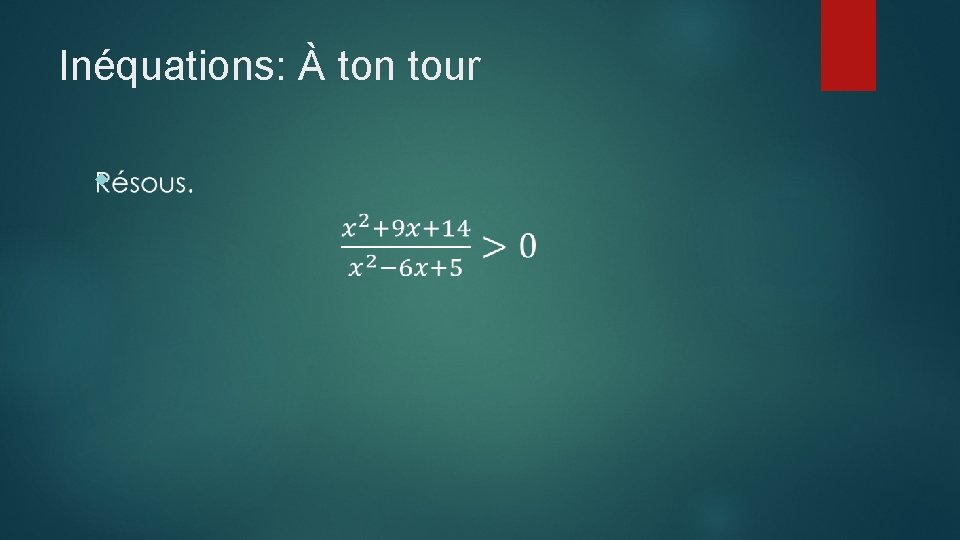









- Slides: 47

Chapitre 3: Les fonctions rationnelles MHF 4 U

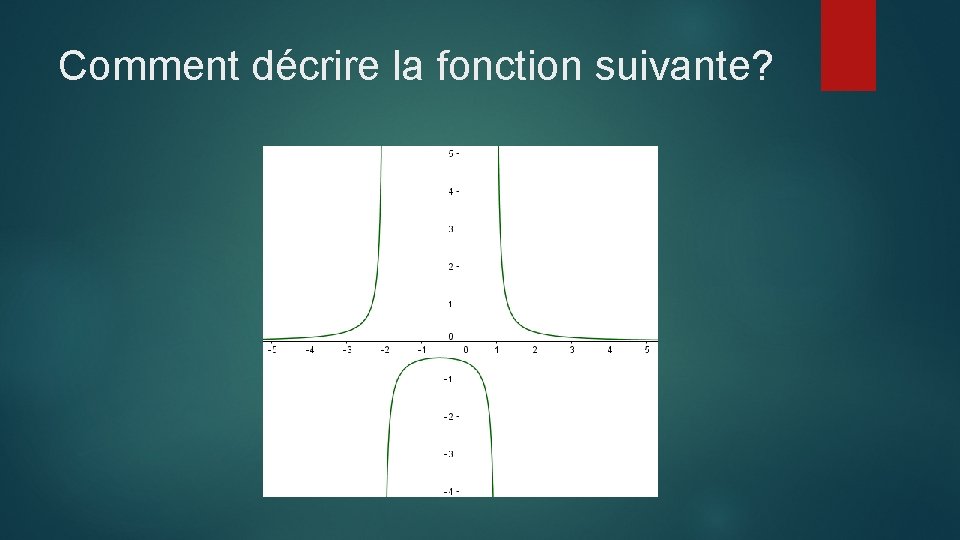
3. 1: L’inverse d’une fonction affine Comment décrire la fonction suivante?

Vocabulaire * Hyperbole: Courbe avec points pour lesquels la différence de distance à 2 points fixes (foyers) est égale. http: //www. alloprof. qc. ca/BV/Pages/m 1329. aspx Asymptote: Droite vers laquelle tend le graphique, sans jamais y toucher.

Inverse d’une fonction affine *

Exemple #1 (p. 149)

Votre tour:

Pente croissante vs décroissante Sur quel intervalle la pente est-elle: Positive? Négative? Croissante? Décroissante?

Exercice #7 a) (ensemble)

Exercice #7 b) (vous)

Votre tour! P. 153 #1 a-b, 2 a-b, 3 a-b, 7 b-c

3. 2: L’inverse d’une fonction du second degré

Comment décrire la fonction suivante?

Questions Où sont les asymptotes? Quel est le comportement du graphique à gauche et à droite de chaque asymptote verticale? Quel est le comportement de la pente (positive ou négative) à gauche de la première asymptote verticale? À droite de la deuxième asymptote verticale?

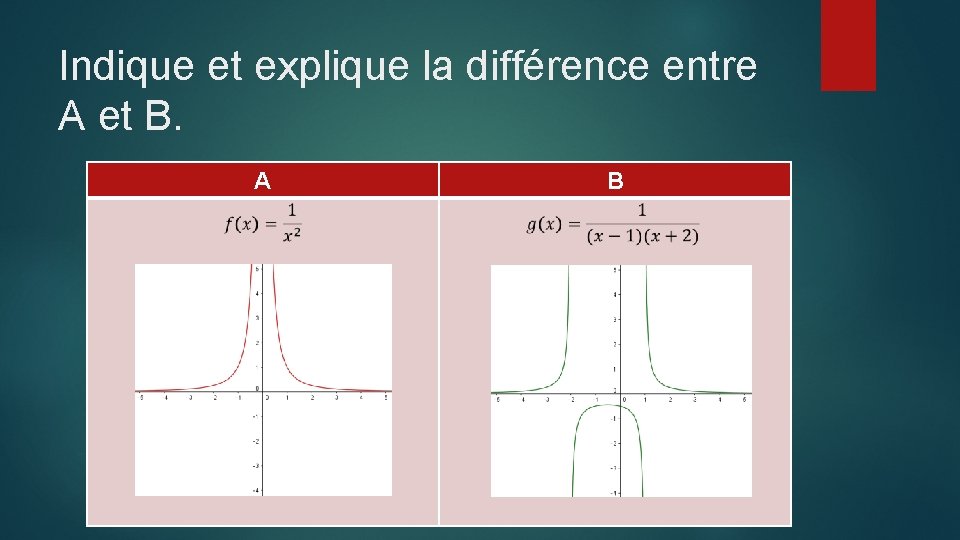
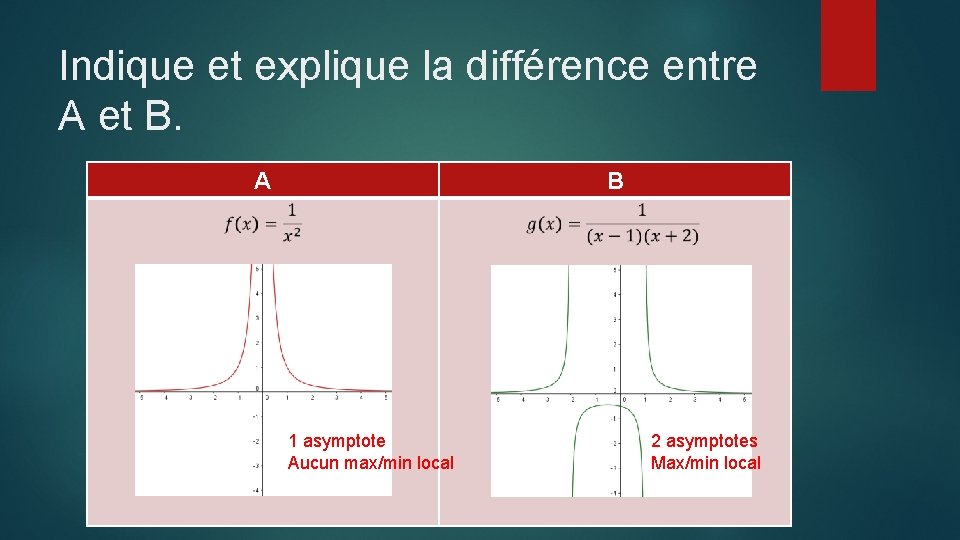
Indique et explique la différence entre A et B. A B

Indique et explique la différence entre A et B. A B 1 asymptote Aucun max/min local 2 asymptotes Max/min local

Comment prédire l’abscisse (x) du max/min local? Exemple #1 • Asymptotes: x = 2, -1 • Maximum local: x = -0. 5 Exemple #2 • Asymptotes: x = 4, 0 • Maximum local: x = -2

Notes * Le graphique de l’inverse d’une fonction de second degré qui admet 2 zéros a: 3 parties Partie centrale a un max/min local. Ce max/min local est à égale distance des asymptotes verticales.

Exemple #1

À votre tour Manuel p. 165 #5 a)

Devoir P. 165 #1 a), 2 b)-c), 3 c), 5 b)-c), 11


Quel est le rôle de b?

Rôles des coefficients * Coefficient A B C D Rôle Étirer la courbe sans modifier les asymptotes, le domaine ou l’image.

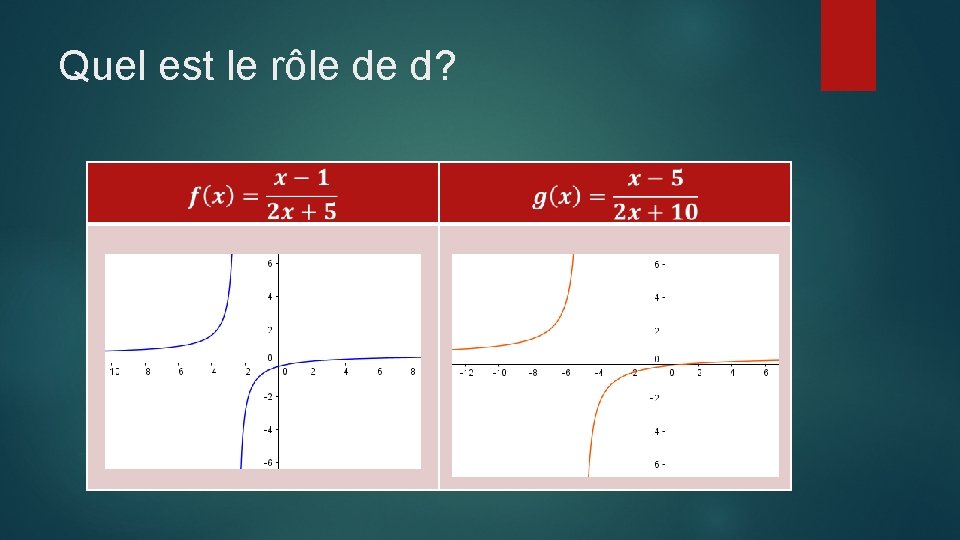
Quel est le rôle de d?

Rôles des coefficients * Coefficient A B C D Rôle Étirer la courbe sans modifier les asymptotes, le domaine ou l’image. Déplace l’asymptote verticale.

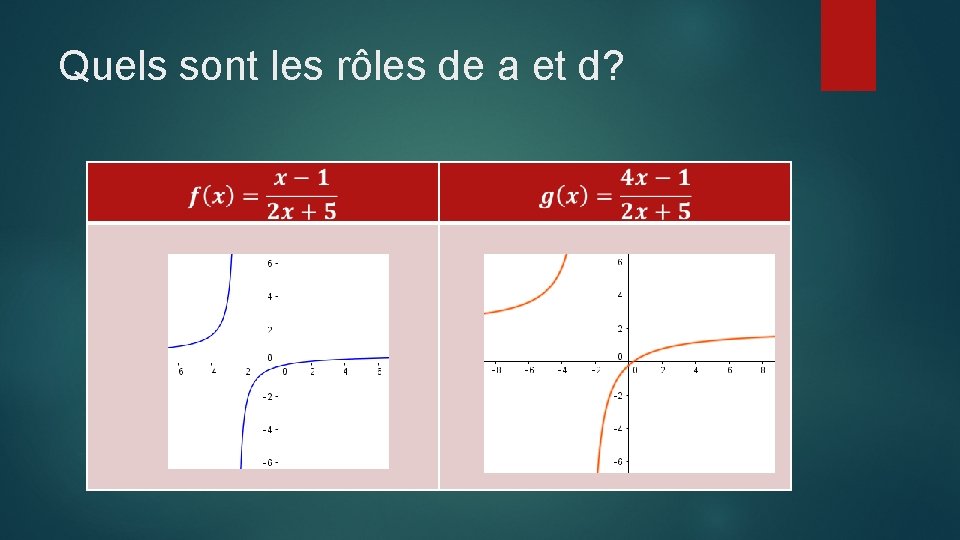
Quels sont les rôles de a et d?

Comment l’expliquer algébriquement? Voir tableau.

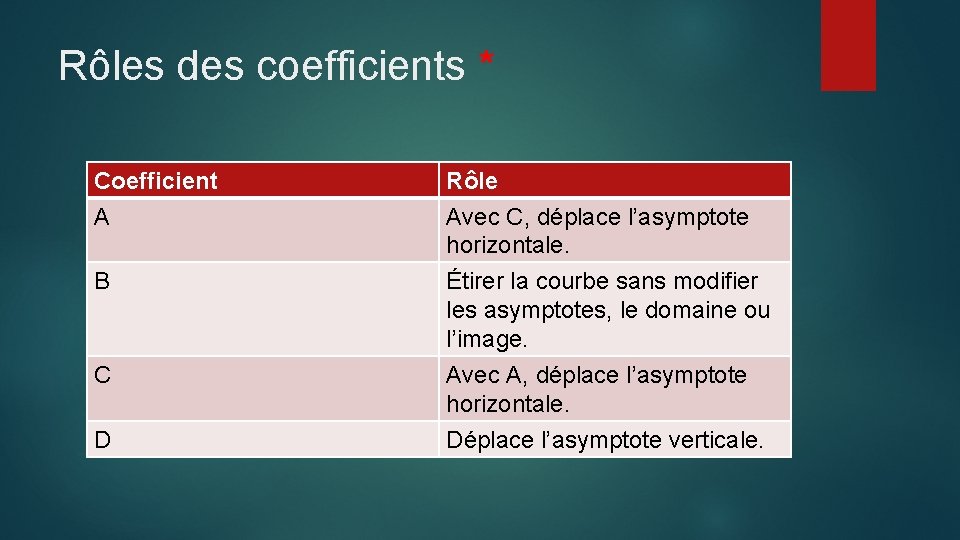
Rôles des coefficients * Coefficient A B C D Rôle Avec C, déplace l’asymptote horizontale. Étirer la courbe sans modifier les asymptotes, le domaine ou l’image. Avec A, déplace l’asymptote horizontale. Déplace l’asymptote verticale.

À votre tour

Votre tâche P. 174 #5 -6 -7 -8 -9

3. 4: La résolution d’équations et d’inéquations rationnelles Équations Inéquations

Équations: Exemple #1 a (p. 177)
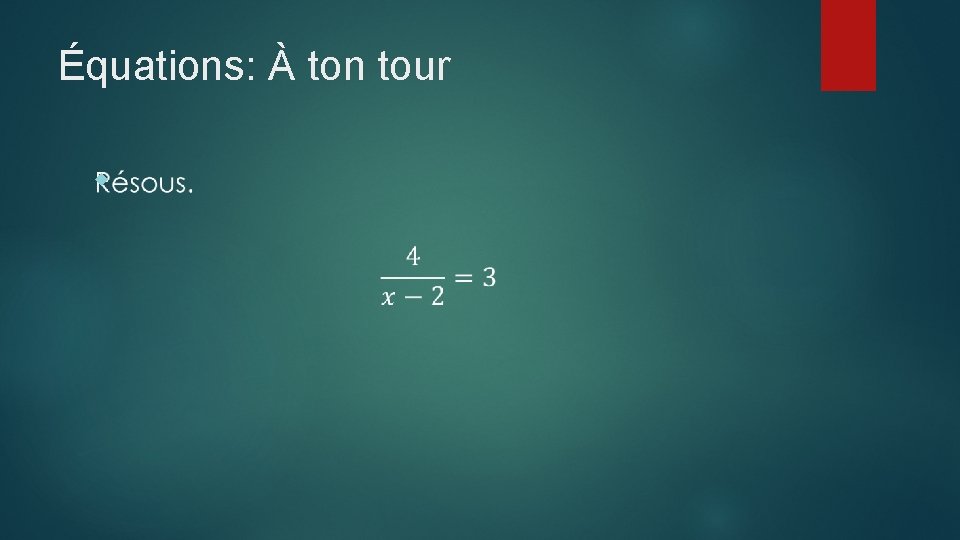
Équations: À ton tour

Équations: Exemple #1 b)
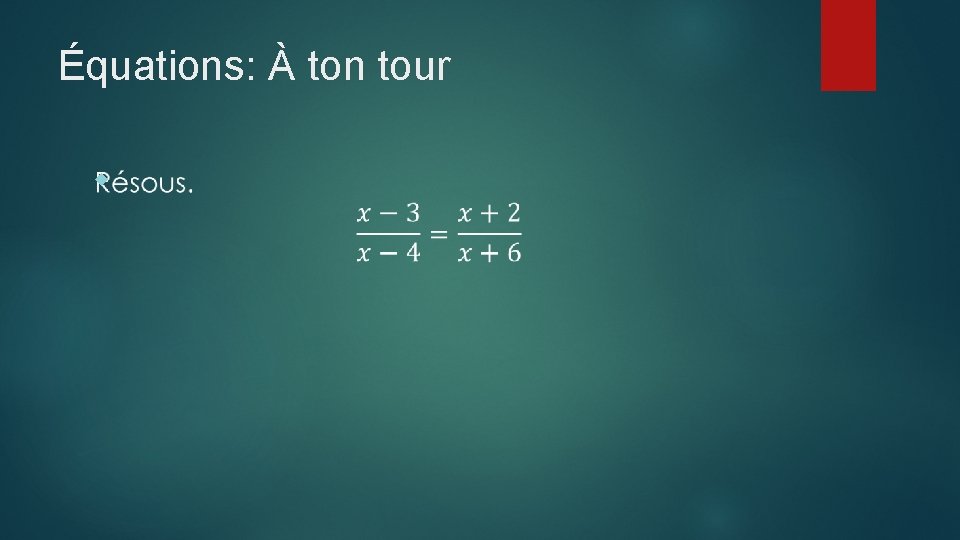
Équations: À ton tour

Pour résoudre une équation * 1. Factoriser numérateur et dénominateur. 2. Multiplier par dénominateurs. 3. Simplifie. 4. Mettre tous les termes d’un côté. 5. Trouver zéros en factorisant ou formule quadratique.

Inéquations: Exemple #4
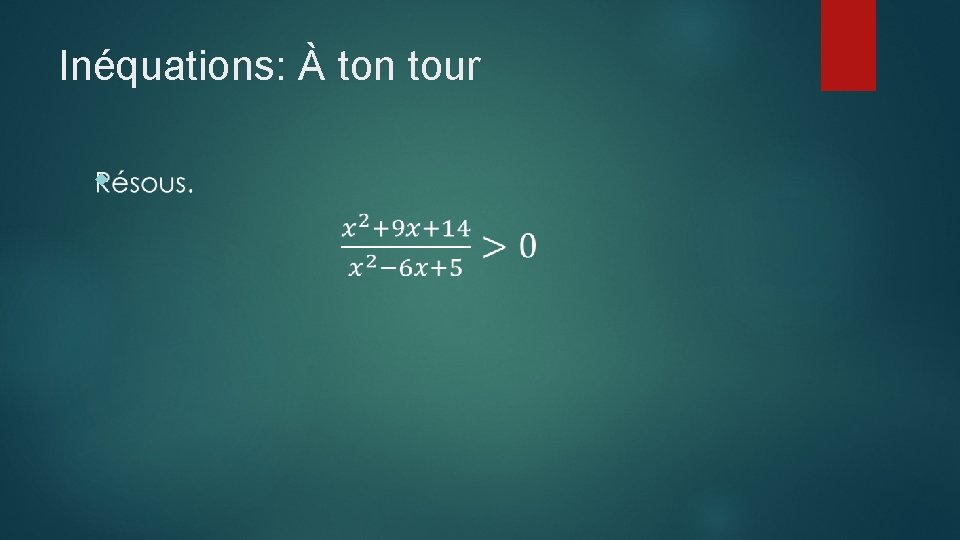
Inéquations: À ton tour

Exercice #7 (p. 184)

Exercices P. 184 #5 b-c-d, 8, 12

3. 5: Les liens avec la vie courante

Exemple #1 (p. 186) L’intensité sonore (en watts par mètre carré) est inversement proportionnelle au carré de la distance (en mètres) de la source du son. L’intensité sonore d’un haut-parleur placé à une distance de 2 m est de 0, 001 W/m 2. a) Détermine une fonction pour représenter cette relation. b) Représente graphiquement cette fonction. c) Quel sera l’effet sur l’intensité sonore si l’on coupe de moitié la distance de la source du son?

À ton tour! (p. 189 #1)

Exemple #2 (p. 187)

À ton tour! (p. 189 #2) Selon la loi de Boyle, à une température constante, le volume d’un gaz varie en raison inverse de la pression exercée sur ce gaz. Un réservoir contient 10 L de gaz hydrogène à une pression de 500 k. Pa. Détermine une fonction qui établit le lien entre le volume et la pression exercée sur ce gaz. Trace un graphique de cette relation en calculant le volume du gaz à différentes pressions atmosphériques. Quel sera l’effet sur le volume du gaz si tu doubles la pression?

Exemple #3 (p. 188)

À ton tour P. 190 #4