Chapitre 3 Le mouvement rectiligne cinmatique une dimension

Chapitre 3 Le mouvement rectiligne (cinématique à une dimension) Cinématique (du grec kinêma=mouvement) : Partie de la physique qui étudie le mouvement des corps, abstraction faite des forces qui le produisent.

3. 1 Position et déplacement Position x : Coordonnée définissant un point de l’espace par rapport à une origine choisie (repère). …les unités de… Rem: Les unités sont DANS les variables; on n’accompagne pas les variables de leurs unités

Déplacement (dépl. résultant) Δx : Changement de position d’un objet, va d’une position initiale à une position finale. Équivalent : x peut être négatif

Distance parcourue Δs : Somme des longueurs des déplacements partiels (toujours positive). (Différent du module du déplacement si un mouvement se fait en plusieurs phases dans des orientations différentes. ) Sommation (pour toutes les phases du mouvement) Valeur absolue = module du déplacement Calcul de la grandeur de la 2 e phase du mouvement … Exemple à venir avec x, x et s.

3. 2 La vitesse moyenne Remarque: Peut être négative. Si on veut désigner la grandeur de la vitesse, on dira « module » de la vitesse. PAS UNE POSITION x SUR UN INSTANT t, mais une DISTANCE x SUR UN INTERVALLE t.

Exemple: Un sprinter court le 100 m en 9, 58 secondes. Quelle est sa vitesse moyenne en km/h?

Conversion courante… (raccourci) Donc: Et:

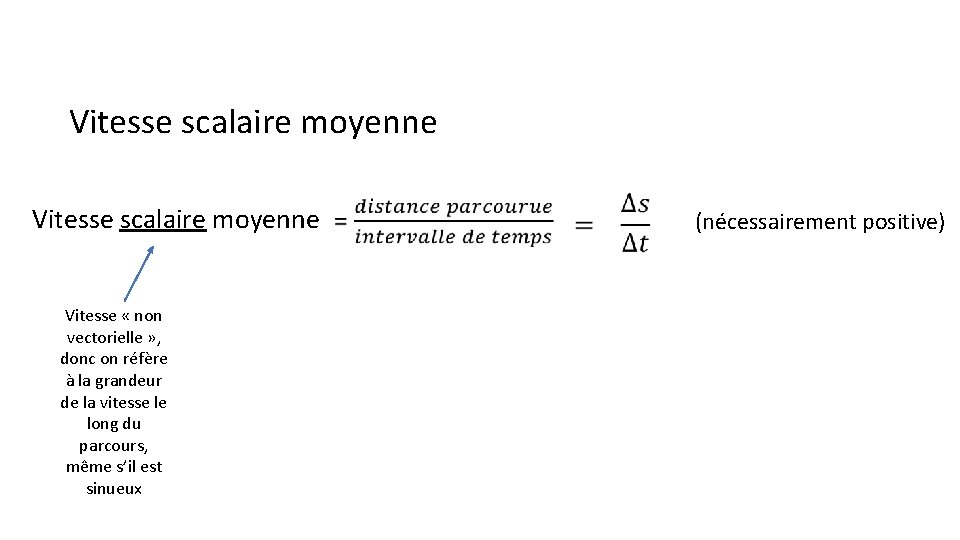
Vitesse scalaire moyenne Vitesse « non vectorielle » , donc on réfère à la grandeur de la vitesse le long du parcours, même s’il est sinueux (nécessairement positive)

Exemple: De Québec (km 305 sur la 40), vous allez à Montréal (km 47) et revenez à Trois-Rivières (km 160) en 3, 5 h. Quelle est la vitesse scalaire moyenne et la vitesse moyenne?

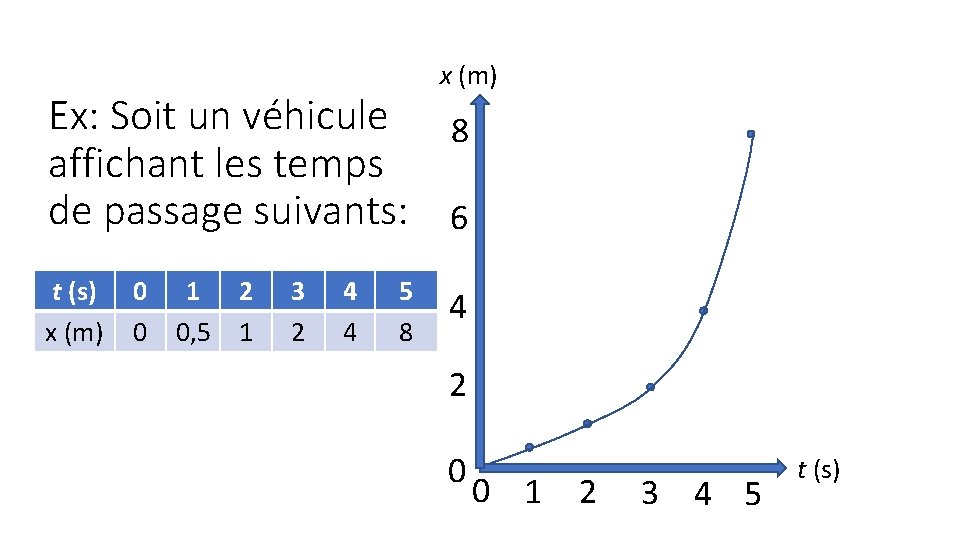
x (m) Ex: Soit un véhicule 8 affichant les temps de passage suivants: 6 t (s) x (m) 0 0 1 0, 5 2 1 3 2 4 4 5 8 4 2 0 0 1 2 3 4 5 t (s)

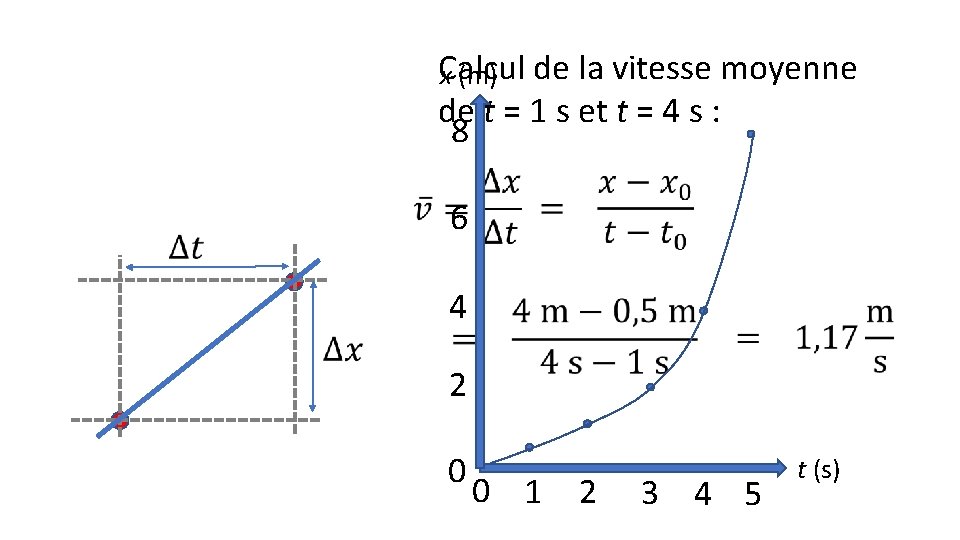
Calcul de la vitesse moyenne x (m) de t = 1 s et t = 4 s : 8 6 4 2 0 0 1 2 3 4 5 t (s)

3. 4 L’accélération

3. 5 Le Mouvement Rectiligne Uniformémént Accéléré Si MRUA a est constante en tout temps

Équations de la cinématique à une dimension: Vitesse moyenne SI MRUA

Équations de la cinématique à une dimension: Vitesse instantanée (vitesse en vigueur à un instant précis) Si MRUA:

Remarque: C’est une équation d’une droite. La vitesse en fonction du temps (v(t)) évolue donc de façon linéaire (MRUA).

Équations de la cinématique à une dimension: Position

Remarque: C’est une équation du second degré. La position en fonction du temps (x(t)) évolue donc de façon quadratique et décrit une parabole (MRUA).

Équations de la cinématique à une dimension: Aussi… Et:

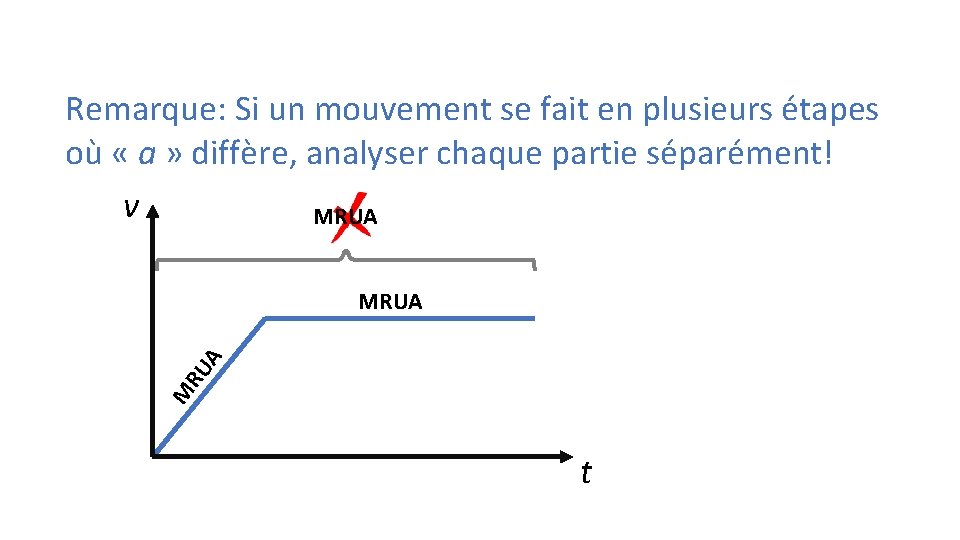
Remarque: Si un mouvement se fait en plusieurs étapes où « a » diffère, analyser chaque partie séparément! v MRUA M RU A MRUA t

Méthode de résolution: Schéma (objets, trajectoire, axes) Identifier le mouvement analysé (début/fin) Liste des paramètres (6) Équations (2 principales et parfois l’une des 2 secondaires) • Calculs • Appréciation du résultat • •

3. 6 Chute libre verticale Sur Terre, pour un axe y positif vers le haut: y

Exemple: Un chat roupille sur une branche à 15 m du sol lorsqu’il roule en bas de la branche. Combien de temps a -t-il pour se retourner sur ses pattes? y 15 m Chute de la branche au sol (15 m à 0) Mouvement? Paramètres Schéma (6) 0

Calculs Équations #1 #2 y Appréciation 15 m Identifier les inconnues L’équation #1 contient une seule inconnue, t. #1: 0

Exemple: Une balle est lancée vers le haut à partir d’un toit de 40 m et arrive au sol en 4, 7 s. a) Quelle est sa hauteur maximale au-dessus du sol? b) Quelle est sa vitesse à 15 m en dessous du niveau du toit? y a) Élévation de y 0 à y 1 Mouvement? Schéma. Paramètres (6)

Calculs Équations y #1 #2 2 équation / 3 inconnues = problème! Plus de deux inconnues dans les 6 paramètres: SOLUTION IMPOSSIBLE! Traiter d’abord un mouvement pour lequel on a assez d’information

Exemple: Une balle est lancée vers le haut à partir d’un toit de 40 m et arrive au sol en 4, 7 s. a) Quelle est sa hauteur maximale au-dessus du sol? Étape préalable: y Mouvement de y 0 à y 3 Il n’est pas nécessaire de séparer le mouvement en 2

Calculs Équations #3 y #3 #4 L’équation #3 ne comporte qu’une inconnue et permet de calculer v 0 :

Calculs Retour sur le #1 mouvement y 0 à #2 Deux inconnues y 1 dont : le temps, dans y On peut utiliser l’équation Appréciation les deux équations fondamentales…

Exemple: Une balle est lancée vers le haut à partir d’un toit de 40 m et arrive au sol en 4, 7 s. a) Quelle est sa hauteur maximale au-dessus du sol? b) Quelle est sa vitesse à 15 m en dessous du niveau du toit? y b) Mouvement de y 0 à y 2 Mouvement? Schéma. Paramètres (6)

Calculs Équations #5 Deux inconnues dont le temps, dans les deux équations fondamentales… y On peut utiliser l’équation #6

Principe de symétrie Lors d’une chute libre (ou tout MRUA), la courbe x(t) est une parabole; pour une même hauteur, les durées et vitesse (module) de chute sont donc égales aux durées et vitesse d’ascension.

Situations à 2 mobiles Quand deux objets sont en mouvement sur un même axe, rédiger paramètres et équations pour chaque objet, pour des intervalles où toutes les accélérations sont constantes. Tracer un graphique v(t) au besoin.

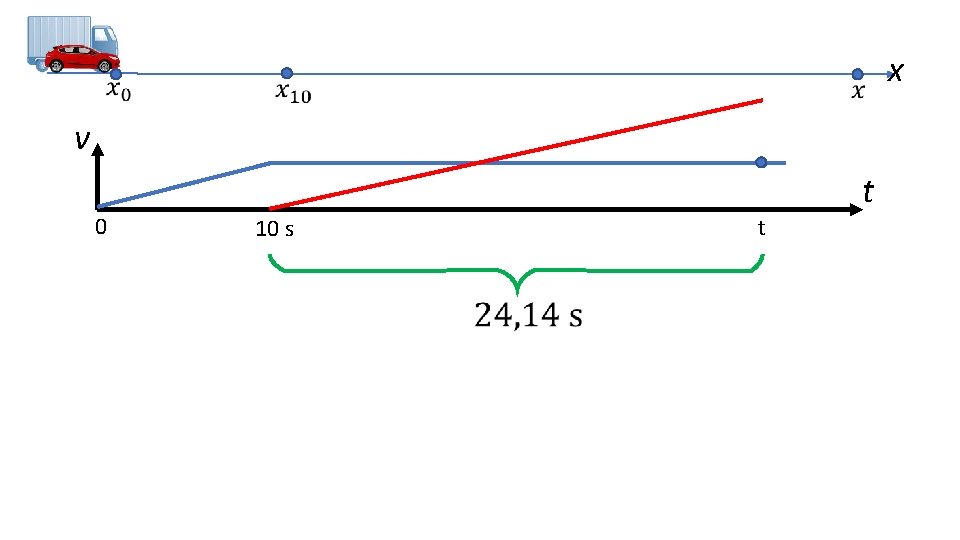
Exemple: Un camion au repos accélère à 1 m/s² et garde une vitesse constante ensuite. Dix secondes plus tard, une auto part du même point et accélère à 2 m/s². Où et quand l’auto rattrape-t-elle le camion? v Schéma 0 10 s x t t

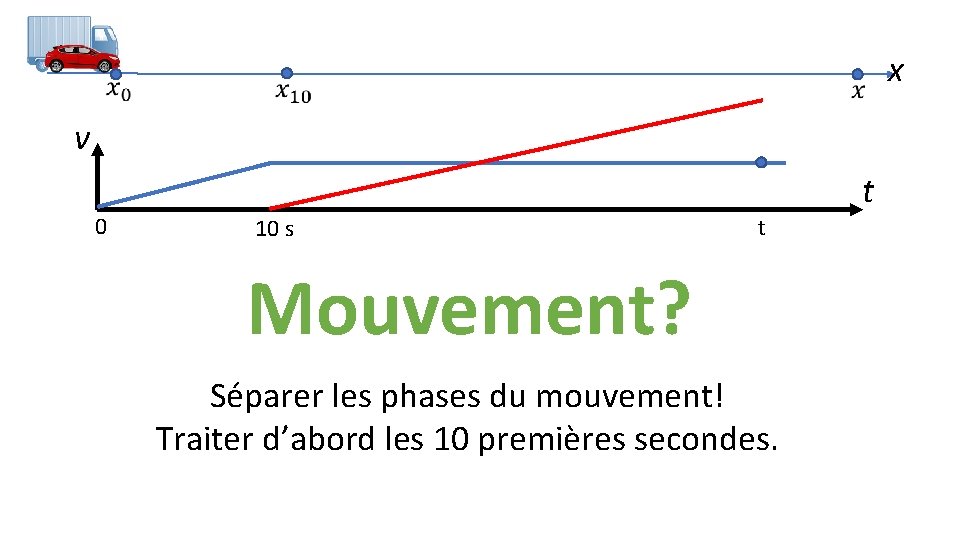
x v 0 t 10 s t Mouvement? Séparer les phases du mouvement! Traiter d’abord les 10 premières secondes.

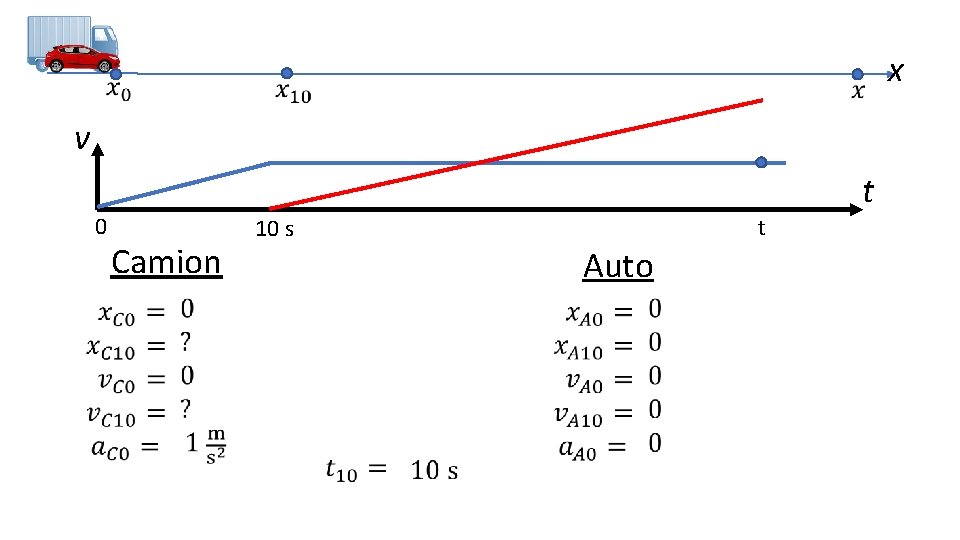
x v 0 t Camion t 10 s Auto

Camion Auto Équations

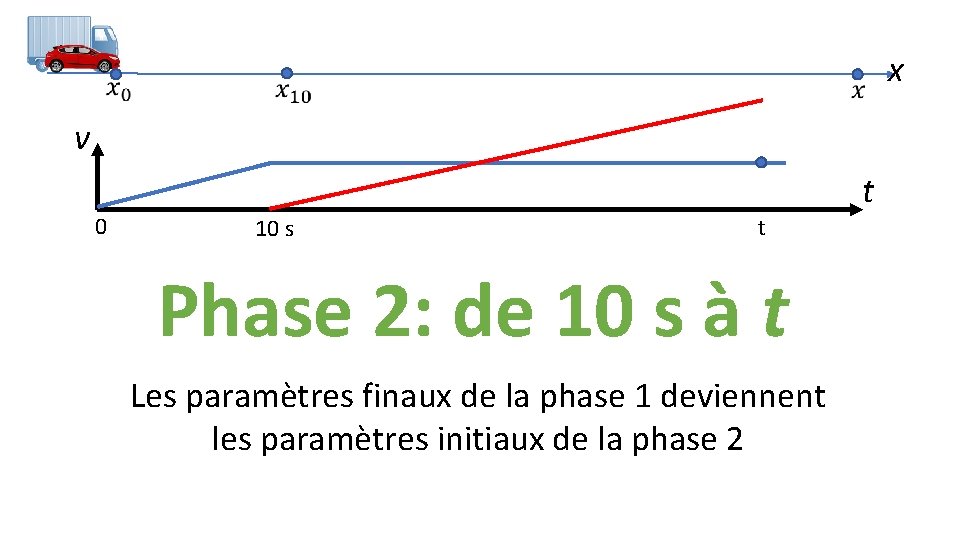
x v 0 t 10 s t Phase 2: de 10 s à t Les paramètres finaux de la phase 1 deviennent les paramètres initiaux de la phase 2

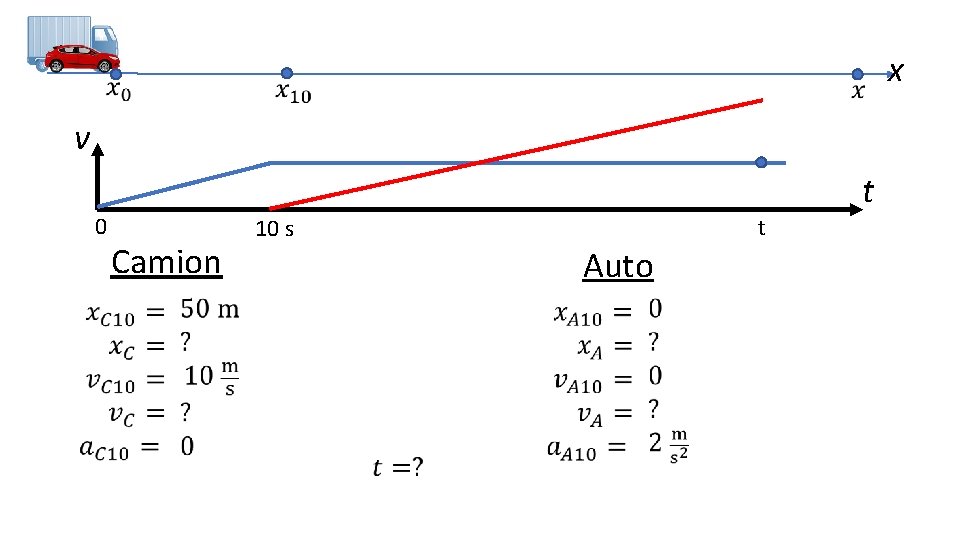
x v 0 t Camion t 10 s Auto

Camion #1 #2 Auto Équations #5 4 Équations / inconnues: 5 (x , t, v , x , v ) C C A A ? ? ? #3 #4

C’est la durée de la 2 e phase: L’auto rattrape le camion 24, 1 s après son départ (l’auto). Donc 34, 1 s après le départ du camion.

x v 0 t t 10 s

Problèmes à 2 scénarios ou 2 étapes Rédiger variables et équations pour chaque scénario/étape.

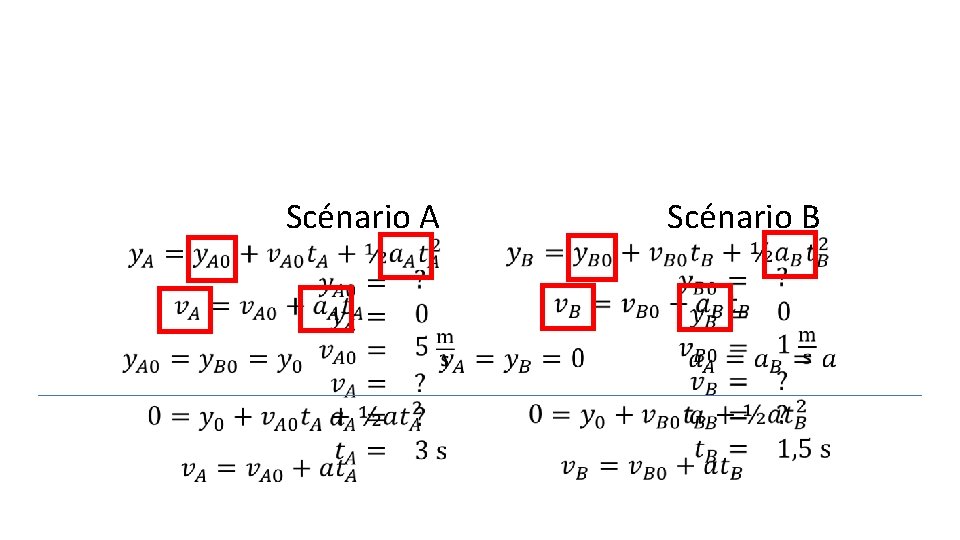
Exemple: Sur la planète mécanos, si on lance d’une certaine hauteur un caillou vers le haut à 5 m/s, il retombe au sol en 3 s. Si on le lance à 1 m/s, il retombe en 1, 5 s. Déterminez l’accélération gravitationnelle. y A B Scénario B Scénario A

Scénario A Scénario B

#3 #4 #1 #2 #1 #3

3. 7 Plans inclinés Un objet pouvant glisser/rouler sans frottement sur un plan incliné subit une accélération constante liée à l’inclinaison :