CHAPITRE 3 Continuit 3 1 Continuit Une premire

CHAPITRE 3: Continuité 3. 1 Continuité Une première définition simple et intuitive de la continuité est la suivante : Si une fonction peut se représenter par une courbe qui n’a pas de coupure, on dit qu’elle est continue. Dans ce cas on peut la tracer sans lever le crayon. * Il faut cependant que la courbe soit une fonction ( le cercle même si on peut le tracer sans lever le crayon n’est pas une fonction continue : ce n’est pas une fonction).

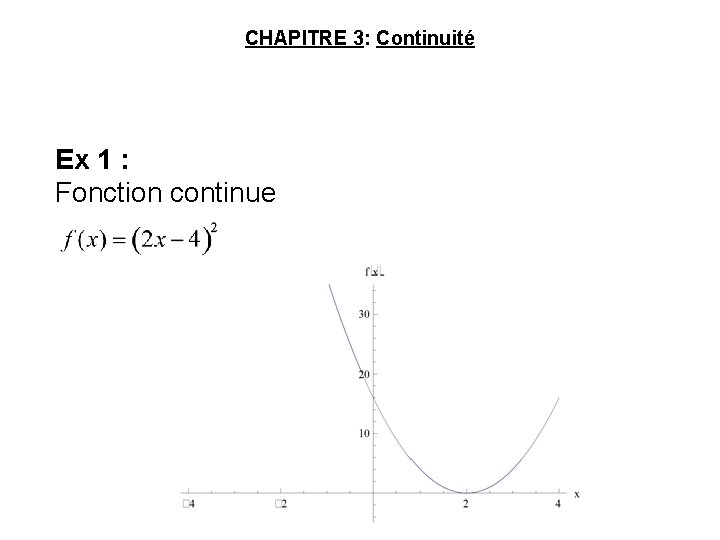
CHAPITRE 3: Continuité Ex 1 : Fonction continue

CHAPITRE 3: Continuité Fonctions possédant une ou des discontinuité

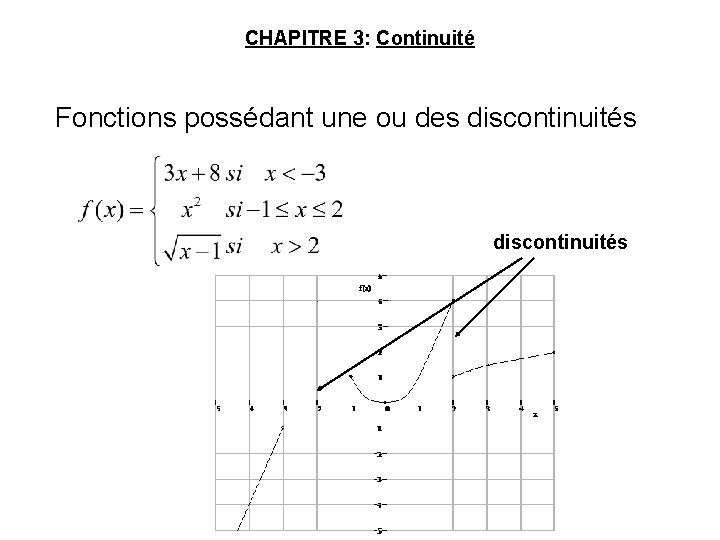
CHAPITRE 3: Continuité Fonctions possédant une ou des discontinuités

CHAPITRE 3: Continuité 3. 2 Rappels #1 Nous avons vu que la valeur vers laquelle tend une fonction f(x) lorsque x s’approche par la droite ou par la gauche d’une certaine valeur a s’appelle la limite unilatérale (à gauche ou à droite selon le cas) de la fonction. Ce qu’on note Ex 1 : limite à droite

CHAPITRE 3: Continuité #2 Nous avons également vu que si la limite au point c de la fonction f(x) vaut ( ), alors il y a une asymptote verticale (droite vers laquelle les points de la fonction s’approchent de plus en plus sans la touchée) en ce point. La fonction n’est cependant pas définie en ce point.

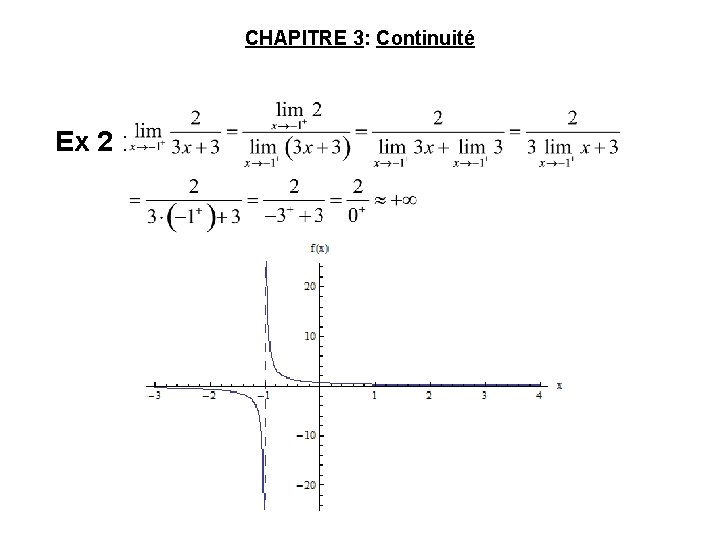
CHAPITRE 3: Continuité Ex 2 :

CHAPITRE 3: Continuité #3 Nous avons vu que la existe si et seulement si. Si ce n’est pas le cas, nous n’évaluerons pas la limite à l’aide des théorèmes car elle n’existe pas.

CHAPITRE 3: Continuité - Ex 3 : n’existe pas car Démonstration : .

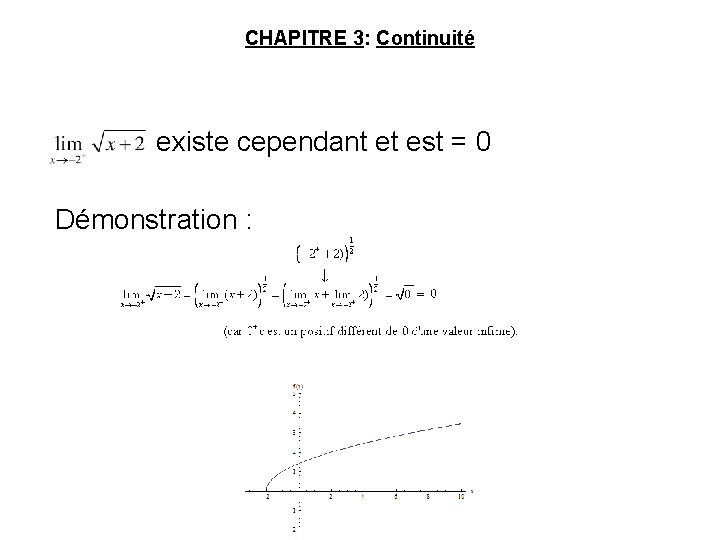
CHAPITRE 3: Continuité existe cependant et est = 0 Démonstration :

CHAPITRE 3: Continuité - Ex 4 : Soit n’existe pas car Démonstration : f(x) ne tend pas vers la même valeur lorsque x s’approche de 0 par la gauche et par la droite

CHAPITRE 3: Continuité 3. 3 Continuité en un point - Nous allons maintenant définir la continuité en un point : Quelles sont les conditions pour qu’une fonction soit continue en un point? est continue au point 1. est définie, donc 2. existe, donc 3. si. . . * Si la fonction n’est pas continue en un point, c’est un point de discontinuité.

CHAPITRE 3: Continuité -Ex 1 : La fonction suivante est-elle continue en x = 2? Pourquoi? Non, car 3 n’est pas respecté discontinuité

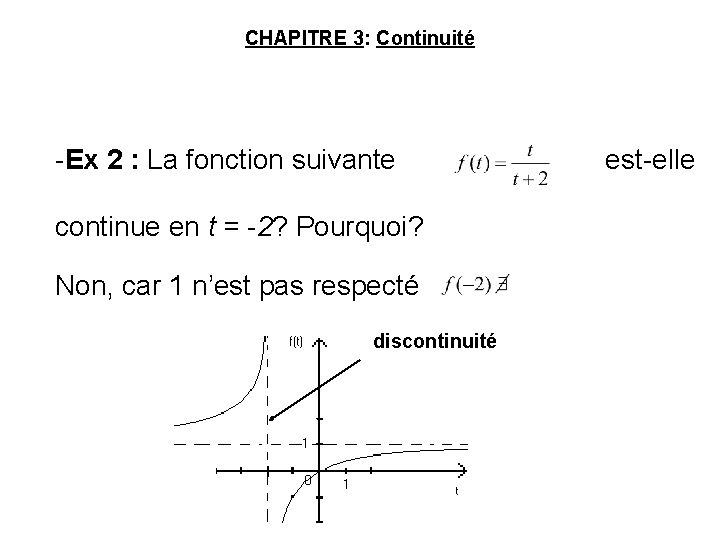
CHAPITRE 3: Continuité -Ex 2 : La fonction suivante continue en t = -2? Pourquoi? Non, car 1 n’est pas respecté discontinuité est-elle

CHAPITRE 3: Continuité -Ex 3 : La fonction suivante est-elle continue en x = 4? Pourquoi? Oui, car 1, 2 et 3 sont respectés continue

CHAPITRE 3: Continuité -Ex 4 : La fonction suivante est-elle continue en x = 3? Pourquoi? Non, car 2 n’est pas respecté discontinuité

CHAPITRE 3: Continuité 3. 4 Continuité sur un intervalle On dit que la fonction est continue sur. si

CHAPITRE 3: Continuité →On doit cher les points où, sur l’intervalle, il pourrait y avoir des discontinuités. Principalement : 1. (les divisions par 0). 2. (les racine carrées et autres racines paires). 3. Les transition des fonctions partie (les bornes). 4. Fonctions logarithmiques ou autres fonctions ayant des restrictions sur le domaine. ( ).

CHAPITRE 3: Continuité 3. 5 Propriétés des fonctions continues Certaines propriétés nous permettent de démontrer facilement la continuité de certaines fonctions (Si on dit d’une fonction qu’elle est continue, on considère alors qu’elle est continue sur l’ensemble de son domaine à moins d’avis contraire).

CHAPITRE 3: Continuité Propriétés des fonctions continues : 1. La fonction constante 2. La fonction identité est continue partout. Si f(x) et g(x) sont continues en x = a: 3. est continue en . 4. est continue en . 5. est continue en , pourvu que .

CHAPITRE 3: Continuité - Ex 1 : Vérifier si est continue au point x = 3. *On verra plus loin qu’on aurait pu seulement dire que comme c’est un polynôme, on peut considérer que la fonction est continue partout!

CHAPITRE 3: Continuité - Ex 2 : Vérifier si est continue au point x = 2.

CHAPITRE 3: Continuité * Des propriétés vues plus haut (Propriétés des fonctions continues ), il découle 2 résultats touchant les fonctions polynomiales et les fonctions rationnelles. Continuité des fonctions polynomiales et des fonctions rationnelles : 1. Une fonction polynomiale ( est un polynôme). est continue partout 2. Une fonction rationnelle tous les x tels que polynômes). est continue pour ( sont des

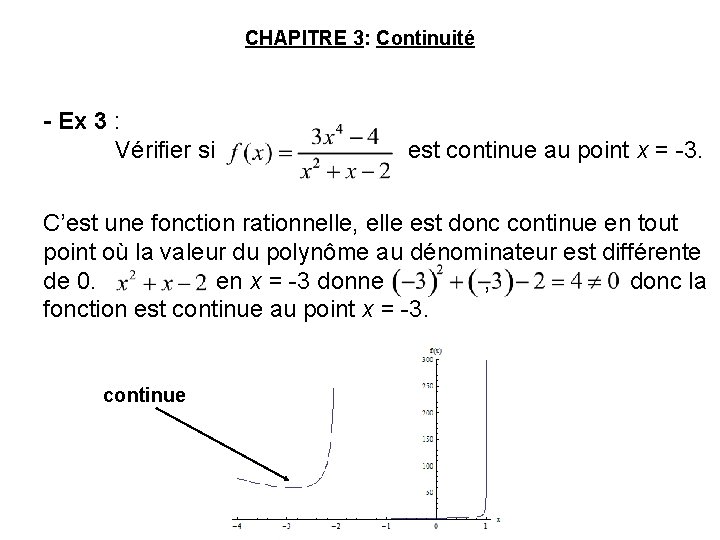
CHAPITRE 3: Continuité - Ex 3 : Vérifier si est continue au point x = -3. C’est une fonction rationnelle, elle est donc continue en tout point où la valeur du polynôme au dénominateur est différente de 0. en x = -3 donne , donc la fonction est continue au point x = -3. continue

CHAPITRE 3: Continuité Théorèmes : Supposons un chat qui se déplace en ligne droite entre 2 points. Le chat part du point A et se rend au point B situé à 2 m devant lui. Le chat peut avancer et reculer, mais ne peut pas disparaître à un endroit et réapparaître plus loin. Il passera donc inévitablement sur tous les points sur la ligne droite entre A et B.

CHAPITRE 3: Continuité Vidéo: Chat

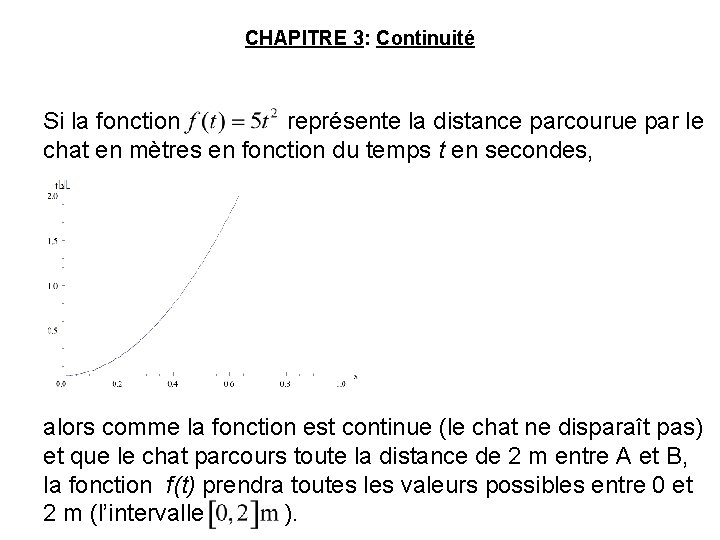
CHAPITRE 3: Continuité Si la fonction représente la distance parcourue par le chat en mètres en fonction du temps t en secondes, alors comme la fonction est continue (le chat ne disparaît pas) et que le chat parcours toute la distance de 2 m entre A et B, la fonction f(t) prendra toutes les valeurs possibles entre 0 et 2 m (l’intervalle ).

CHAPITRE 3: Continuité Cet exemple nous permet d’introduire le théorème des valeurs intermédiaires : Théorème des valeurs intermédiaires Soit f une fonction continue sur un intervalle fermé et soit N un nombre quelconque entre f(a) et f(b). Alors il existe au moins un nombre tel que. (Toutes les valeurs de l’image de f(x), entre f(a) et f(b), sont prises par la fonction f. ) *Il peut y avoir plus d’un nombre qui fait que .

CHAPITRE 3: Continuité - Ex 4 : (polynôme) sur une fonction continue et Il y a 3 valeurs de x qui font que f(x)=4 dans l’intervalle.

CHAPITRE 3: Continuité Du dernier théorème, il découle un théorème pour le cas particulier N = 0 Théorème 5 (existence des zéros d’une fonction continue) Si f est une fonction continue sur un intervalle fermé et si f(a) et f(b) sont de signes opposés, alors la fonction f(x) s’annule au moins une fois dans l’intervalle ouvert. *Il peut y avoir plus d’un nombre tel que .

CHAPITRE 3: Continuité - Ex 5 : (polynôme) sur une fonction continue et Il y a 1 zéro dans l’intervalle.

CHAPITRE 3: Continuité - Exercice 1 : Pouvez vous déterminer (à l’aide du théorème sur l’existence des zéros d’une fonction continue) si les 2 fonctions suivantes possèdent au moins une racine dans l’intervalle :

CHAPITRE 3: Continuité a) Trouver si la fonction est continue. b) Trouver si f(0) et f(2) sont de signes opposés. On peut voir qu’en fait f(x) ne s’annule pas sur cet intervalle

CHAPITRE 3: Continuité a) Trouver si la fonction est continue. b) Trouver si g(0) et g(2) sont de signes opposés. On peut voir que g(x) s’annule sur cet intervalle

CHAPITRE 3: Continuité -Est-ce que si on a une fonction continue sur avec et de même signe, on peut conclure qu’il n’y a pas de racine? Non, reprenons par exemple la fonction sur. Elle s’annule en 2 points malgré que La fonction s’annule