CHAPITRE 2 LA THEORIE DU PRODUCTEUR Ch 2

CHAPITRE 2 LA THEORIE DU PRODUCTEUR Ch. 2 - La théorie du producteur 1

Rapprochement de la théorie du consommateur : acteur rationnel avec un objectif de maximisation sous contrainte Réflexion sur le rôle et la place du producteur (Say) Entrepreneurs d'industrie. Ils concourent à la production en appliquant les connaissances acquises, le service des capitaux et celui des agents naturels, à la confection des produits auxquels les hommes attachent une valeur Il s'agit de mettre enjeu quelquefois un très grand nombre d'individus; il faut acheter ou faire acheter des matières premières, réunir des ouvriers, cher des consommateurs, avoir un esprit d'ordre et d'économie Ch. 2 - La théorie du producteur 2

Producteur acquiert sur un marché des facteurs de production et les utilise (combinaison) pour produire afin de vendre Donc triple question à traiter : - conditions de l’efficacité technique de la production (fonction de production) - conditions de l’efficacité économique (comment produire au moindre coût ? ) - quelle quantité produite permet de maximiser le profit ? Ch. 2 - La théorie du producteur 3

1 - La fonction de production 1. 1 Les caractéristiques de la fonction de production Définition de la fonction de production : relation mathématique établie entre la quantité produite et le ou les facteurs de production utilisés, ou encore entre l’output et les inputs. Q = f(K, L) Hypothèses fondamentales Facteurs de production sont substituables Facteurs de production sont divisibles Fonction de production est efficace Distinction long terme – court terme Ch. 2 - La théorie du producteur 4

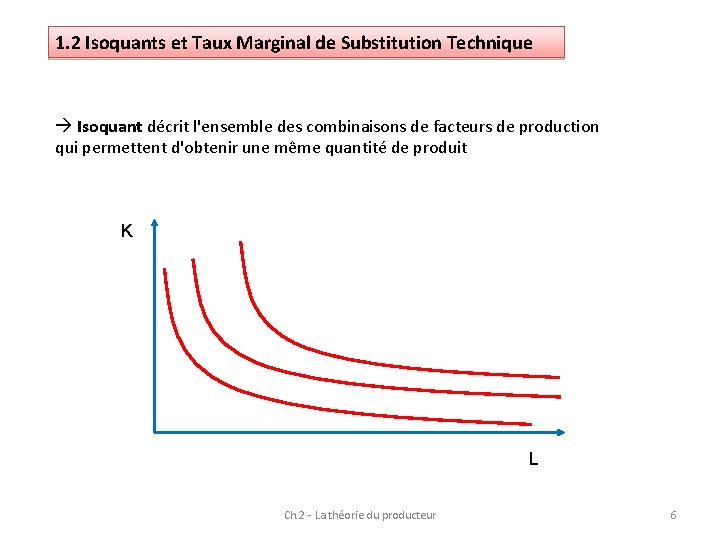
1. 2 Isoquants et Taux Marginal de Substitution Technique Isoquant décrit l'ensemble des combinaisons de facteurs de production qui permettent d'obtenir une même quantité de produit K L Ch. 2 - La théorie du producteur 6

Isoquants présentent des caractéristiques comparables à celles des courbes d'indifférences Isoquants sont décroissants Isoquants ne peuvent se couper Plus un isoquant est éloigné de l'origine, plus la production correspondante est élevée Isoquants sont convexes par rapport à l'origine Ch. 2 - La théorie du producteur 8

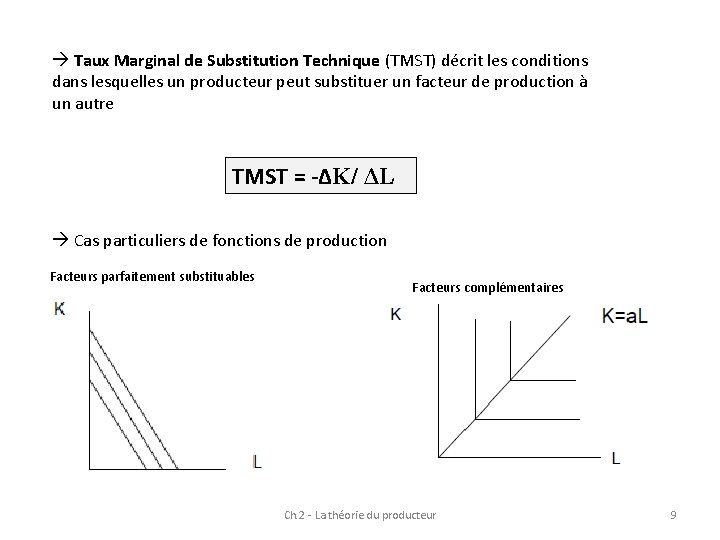
Taux Marginal de Substitution Technique (TMST) décrit les conditions dans lesquelles un producteur peut substituer un facteur de production à un autre TMST = -ΔK/ ΔL Cas particuliers de fonctions de production Facteurs parfaitement substituables Facteurs complémentaires Ch. 2 - La théorie du producteur 9

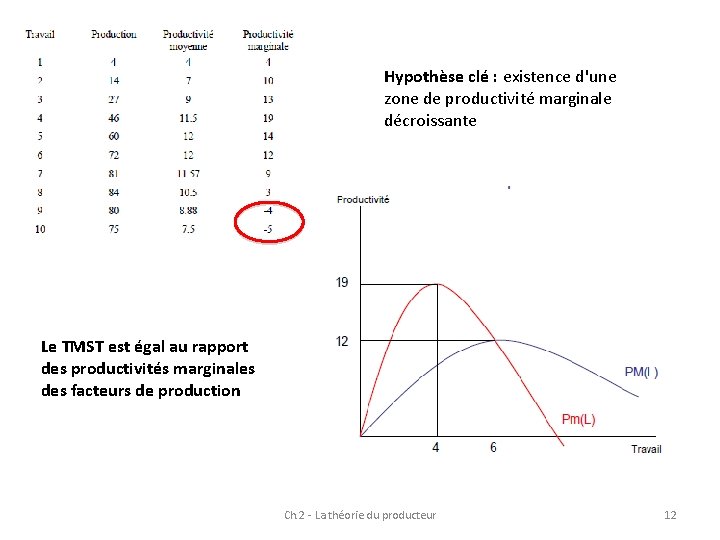
1. 3 Productivité et rendements 1 - Productivité mesure l'impact d'un facteur sur la production totale Productivité moyenne : rapport entre la quantité produite et la quantité d'un facteur utilisé (rendement factoriel) Productivité marginale : rapport entre la variation de la quantité produite et la variation de la quantité d'un facteur utilisé (l'autre restant constant) Ch. 2 - La théorie du producteur 11

Hypothèse clé : existence d'une zone de productivité marginale décroissante Le TMST est égal au rapport des productivités marginales des facteurs de production Ch. 2 - La théorie du producteur 12

2 - Rendements d'échelle : variation de la production lorsque les facteurs de production varient de manière proportionnelle rendements d'échelle constants : production augmente dans la même proportion que les facteurs : Q(m. L, m. K) = m. Q(L, K) rendements d'échelle décroissants : production augmente dans une proportion moindre que les facteurs : Q(m. L, m. K) < m. Q(L, K) rendements d'échelle croissants : production augmente dans une proportion plus forte que les facteurs : Q(m. L, m. K) > m. Q(L, K) Ch. 2 - La théorie du producteur 14

2 - Les fonctions de coût Définition simple : relation entre quantités produites et coûts 2. 1 Coûts fixes et coûts variables Coûts variables sont proportionnels à la quantité produite Coûts fixes sont supportés par l'entreprise quelle que soit la quantité produite nécessité de distinguer parmi les coûts fixes, les "coûts fixes irrecouvrables" ( "sunk costs") Ch. 2 - La théorie du producteur 16

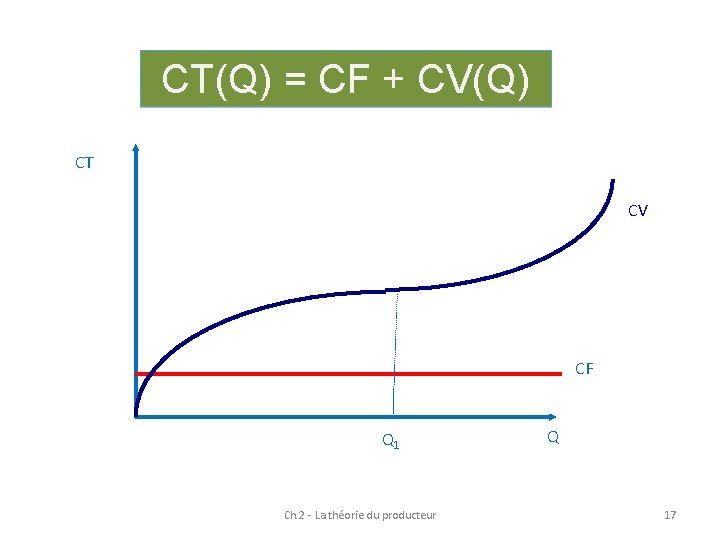
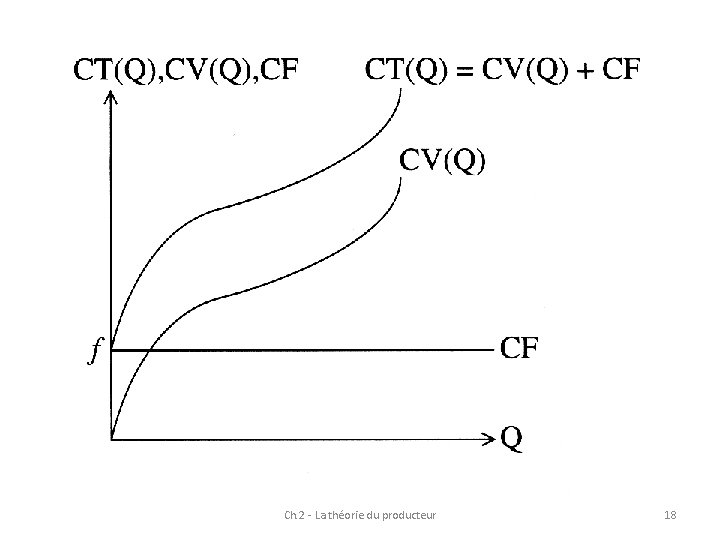
CT(Q) = CF + CV(Q) CT CV CF Q 1 Ch. 2 - La théorie du producteur Q 17

Ch. 2 - La théorie du producteur 18

2. 2 Coûts moyens et coûts marginaux Le coût moyen de production (CM) est défini comme le coût total par unité produite Possibilité de calculer le coût fixe moyen (monotone décroissant) et le coût variable moyen Ch. 2 - La théorie du producteur 19

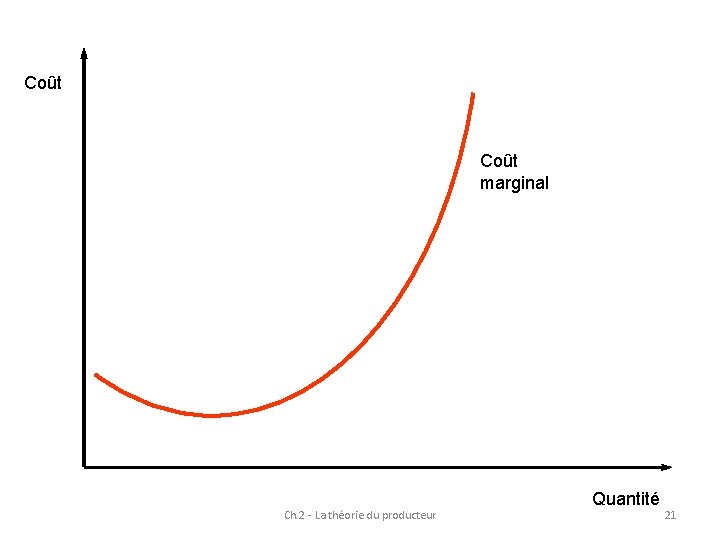
Le coût marginal de production (Cm) est défini comme le coût de la dernière unité produite Coût marginal correspond à la dérivée de la fonction de coût total Ch. 2 - La théorie du producteur 20

Coût marginal Ch. 2 - La théorie du producteur Quantité 21

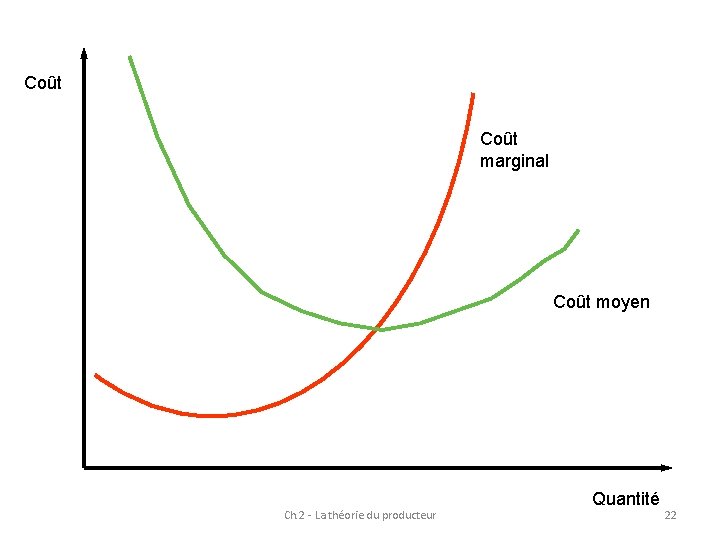
Coût marginal Coût moyen Ch. 2 - La théorie du producteur Quantité 22

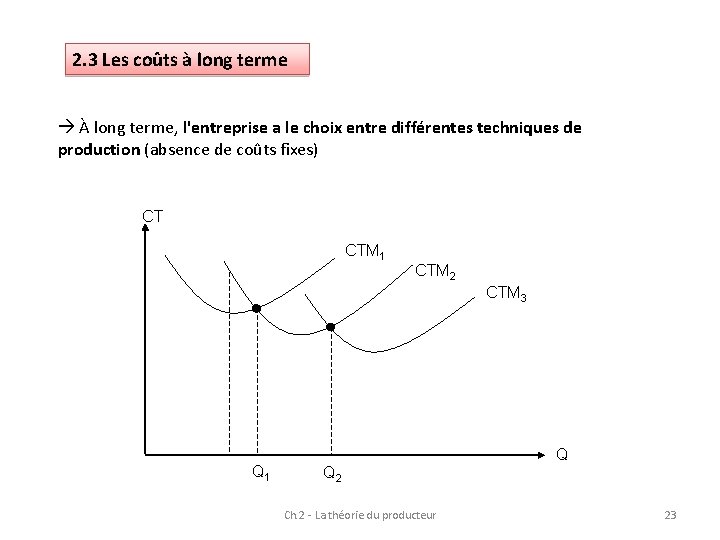
2. 3 Les coûts à long terme À long terme, l'entreprise a le choix entre différentes techniques de production (absence de coûts fixes) CT CTM 1 CTM 2 CTM 3 Q 1 Q Q 2 Ch. 2 - La théorie du producteur 23

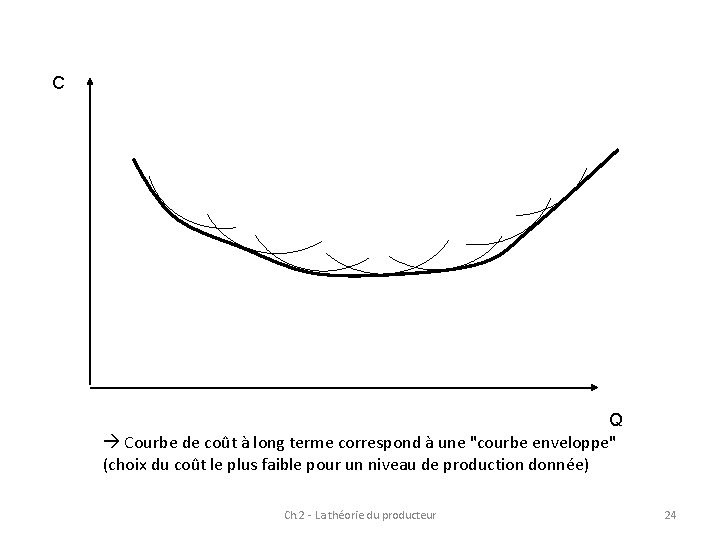
C Q Courbe de coût à long terme correspond à une "courbe enveloppe" (choix du coût le plus faible pour un niveau de production donnée) Ch. 2 - La théorie du producteur 24

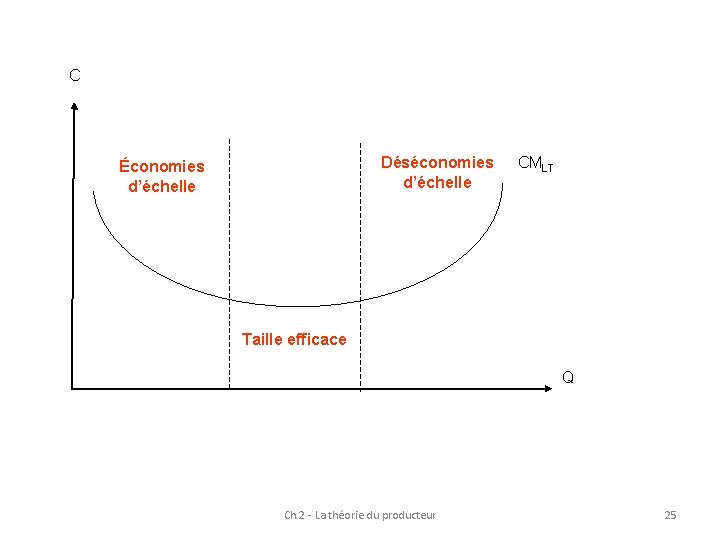
C Déséconomies d’échelle Économies d’échelle CMLT Taille efficace Q Ch. 2 - La théorie du producteur 25

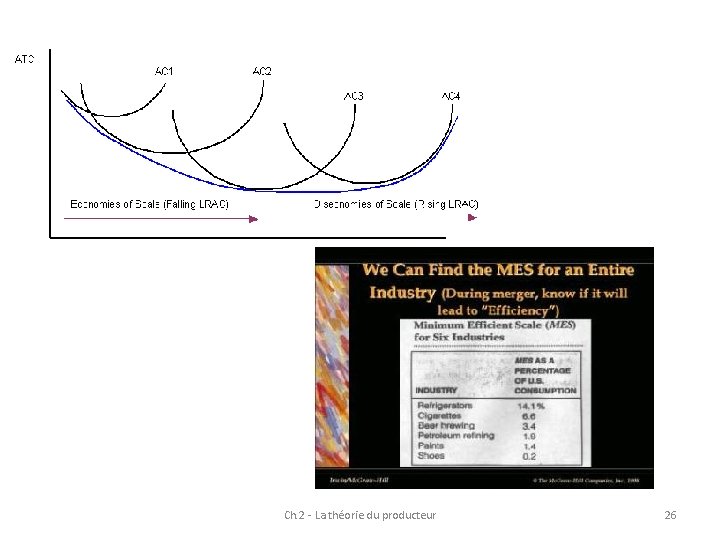
Ch. 2 - La théorie du producteur 26

3 - La détermination de la combinaison productive quelle combinaison de facteurs de production permet de minimiser les coûts pour une production donnée ? 3. 1 La détermination de la dépense du producteur D= w. L+r. K Avec w salaire – r taux d'intérêt Détermination d'une droite d'isocoût (ensemble des combinaisons de facteurs de production correspondant au même coût de production) K = - w/r L + D/r Ch. 2 - La théorie du producteur 27

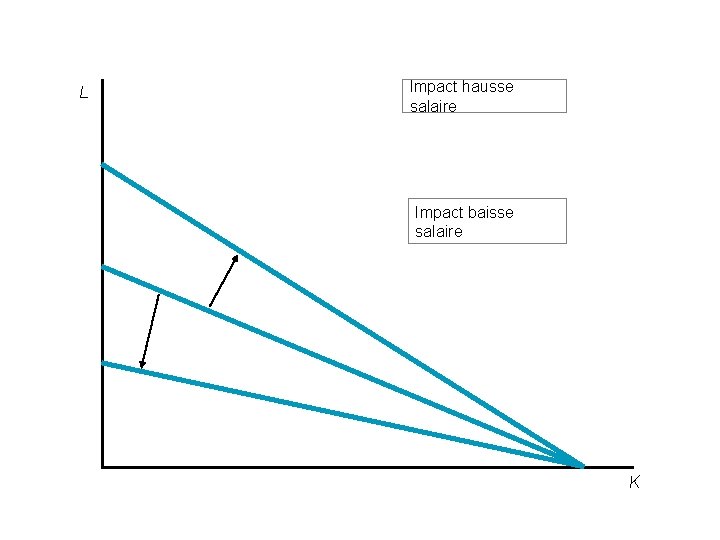
L Impact hausse salaire Impact baisse salaire K

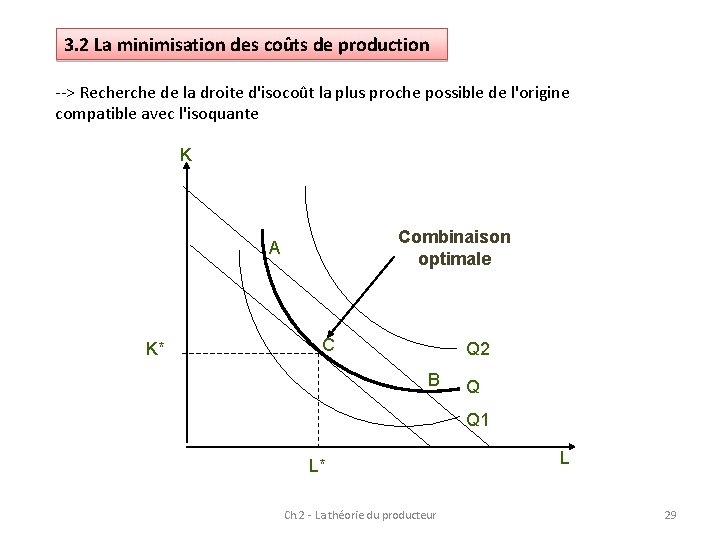
3. 2 La minimisation des coûts de production --> Recherche de la droite d'isocoût la plus proche possible de l'origine compatible avec l'isoquante K Combinaison optimale A K* C Q 2 B Q Q 1 L* Ch. 2 - La théorie du producteur L 29

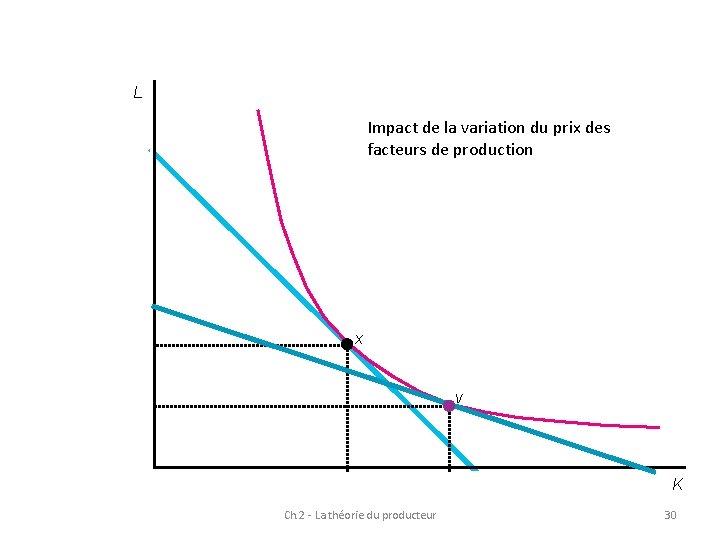
L Impact de la variation du prix des facteurs de production x v K Ch. 2 - La théorie du producteur 30

Combinaison de production optimale pour l'entreprise correspond au point de tangence entre l'isoquante choisie et la droite d'isocoût la plus proche de l'origine Pente de l'isoquante correspond au TMST + TMST est égal au rapport des productivités marginales des facteurs TMST = - ΔK/ ΔL = Pm. L/ Pmk Pente de la droite d'isocoût correspond au rapport du prix des facteurs : - w/r On a donc : Pm. L/ Pm. K = w/ r Pm. L/ w = Pm. K/r Ch. 2 - La théorie du producteur 31

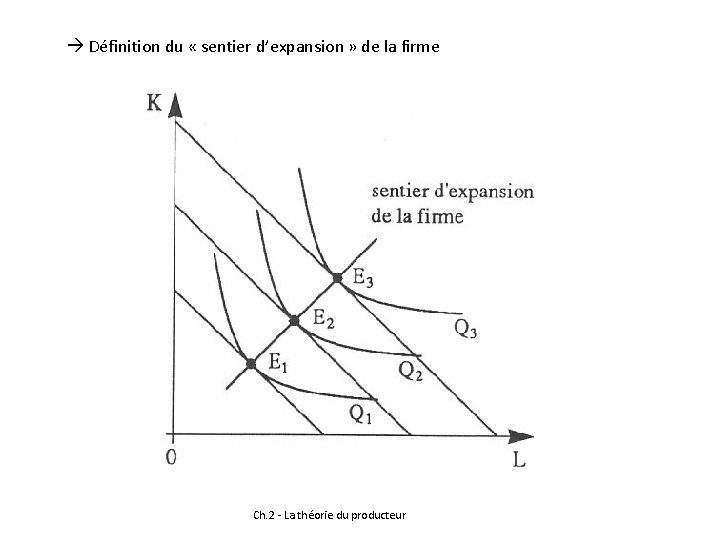
Définition du « sentier d’expansion » de la firme Ch. 2 - La théorie du producteur

4 - La maximisation du profit pour le producteur Hypothèse fondamentale : prix de vente est une donnée qui s'impose au producteur Objectif du producteur : maximiser le profit (défini comme la différence entre les recettes et les coûts) Question : quelle quantité produire pour maximiser le profit ? Ch. 2 - La théorie du producteur 34

En zone de coût marginal décroissant Si la production Q est rentable, alors la production Q + 1 l'est également Recette marginale (p) est la même mais coût de production est plus faible En zone de coût marginal croissant Si la production Q est rentable, alors la production de Q + 1 sera moins rentable Recette marginale (p) est la même mais coût de production est plus élevé P – Cm(Q) > P – Cm (Q+1) > P – Cm(Q+2) … Ch. 2 - La théorie du producteur 35

Production sera poussée jusqu'au niveau tel que P- Cm (Q) = 0 Soit P = Cm (Q) Niveau de production qui maximise le profit est tel que le coût marginal soit égal au prix Ch. 2 - La théorie du producteur 36

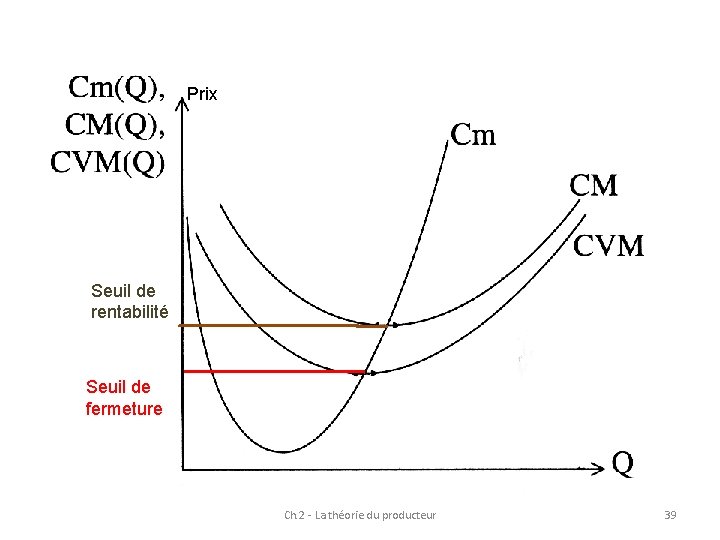
N. B. 1 Raisonnement précédent suppose qu'il existe un niveau de production qui permette un profit positif P Q – CT (Q) > O Ou Q ( P – CM(Q)) > O Existence du profit suppose que le prix de vente du produit est supérieur au coût moyen de production Détermination du seuil de rentabilité : minimum de la courbe de coût moyen Ch. 2 - La théorie du producteur 37

N. B. 2 Dans certains cas, il est possible de produire à perte Production nulle (fermeture) implique un perte égale aux coûts fixes Si la production entraîne une perte inférieure aux coûts fixes, il est possible de continuer à produire PQ – CF – CV (Q) > - CF Ou PQ – CV (Q) > O Détermination du seuil de fermeture : minimum de la courbe de coût variable moyen Soit P > CV (Q) / Q Ch. 2 - La théorie du producteur 38

Prix Seuil de rentabilité Seuil de fermeture Ch. 2 - La théorie du producteur 39

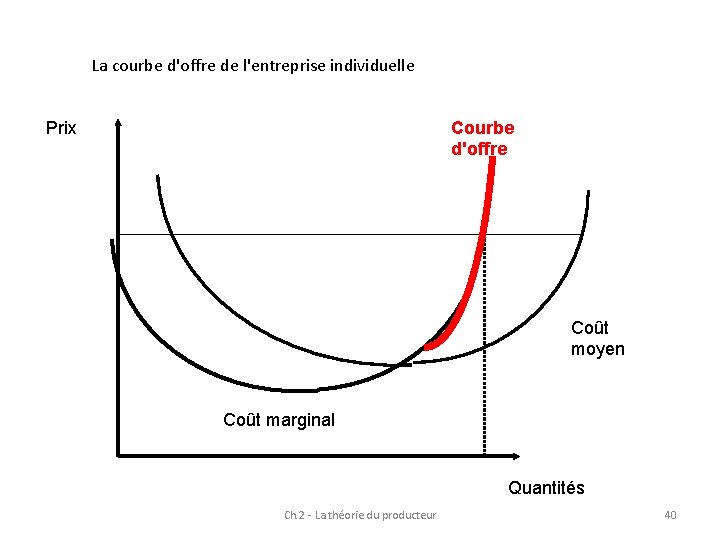
La courbe d'offre de l'entreprise individuelle Prix Courbe d'offre Coût moyen Coût marginal Quantités Ch. 2 - La théorie du producteur 40