Chapitre 11 Vecteurs et repres du plan I

Chapitre 11: Vecteurs et repères du plan:

I. 1) Généralités Repères: Définition: On dit qu’un repère du plan (O, I, J) est orthonormé lorsque : è Les axes des abscisses et des ordonnées sont perpendiculaires, c’est à dire (OI) (OJ). è Les unités de longueur sont les mêmes sur les deux axes c’est à dire OI = OJ. I et J sont toujours les points de coordonnées respectives (1 ; 0) et (0 ; 1).

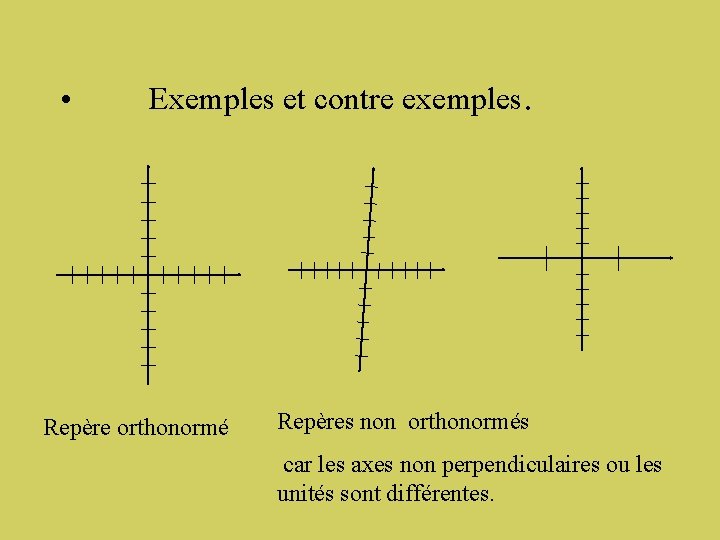
• Exemples et contre exemples. Repère orthonormé Repères non orthonormés car les axes non perpendiculaires ou les unités sont différentes.

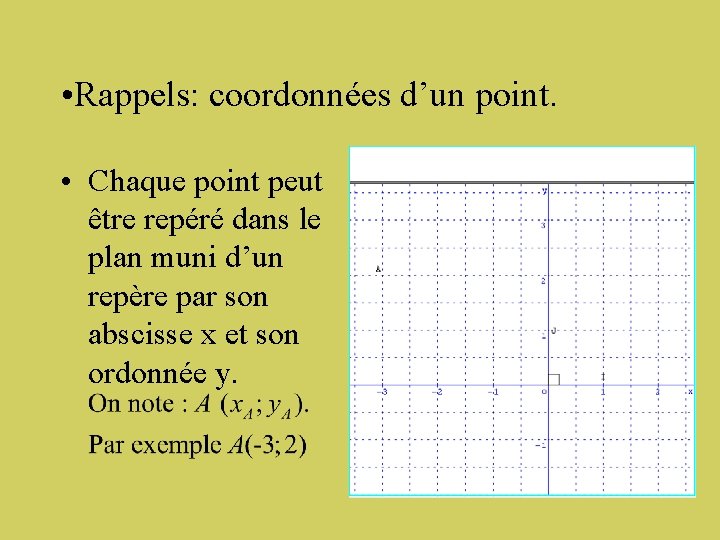
• Rappels: coordonnées d’un point. • Chaque point peut être repéré dans le plan muni d’un repère par son abscisse x et son ordonnée y.

II. Coordonnées d’un vecteur dans un repère.

II. Coordonnées d’un vecteur dans un repère. 1) Définition : Les coordonnées d’un vecteur dans un repère décrivent un déplacement horizontal puis vertical. (point de départ point d’arrivée) Ainsi, un déplacement de « 3 unités vers la droite et 2 unités vers le bas » sera représenté par un vecteur de coordonnées (3 ; -2).

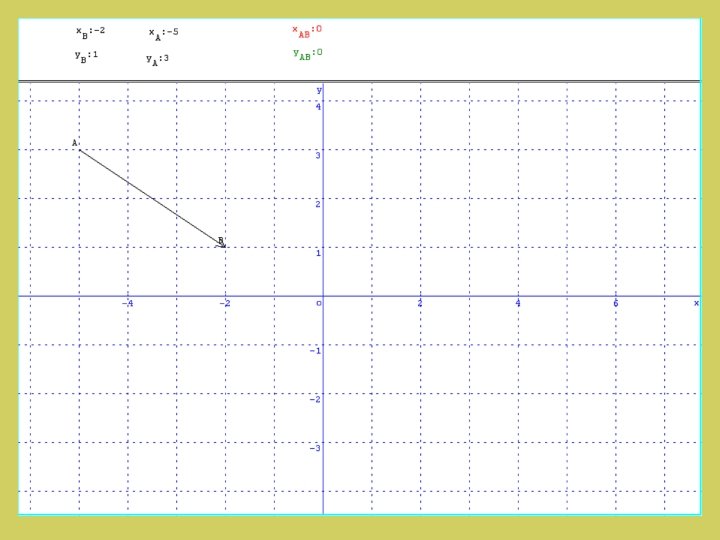
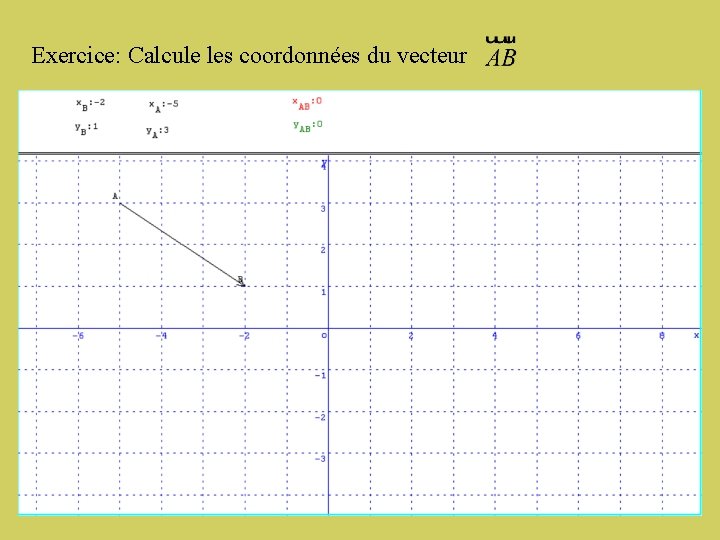
Exercice: Calcule les coordonnées du vecteur

2) Calcul des coordonnées d’un vecteur.

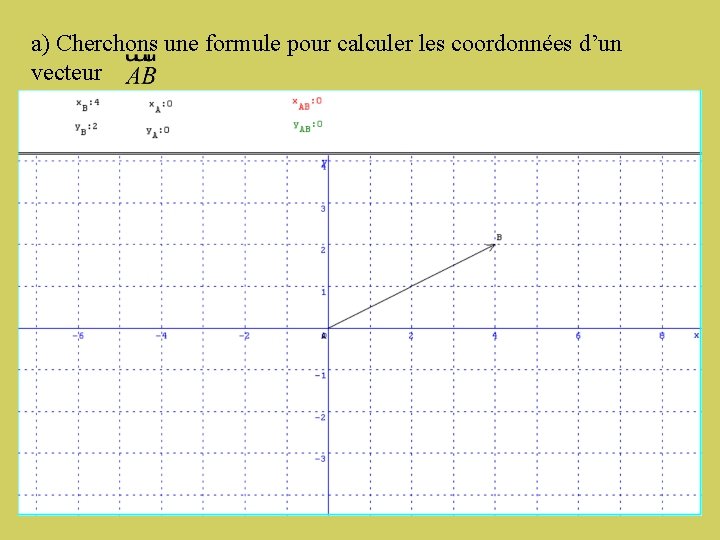
a) Cherchons une formule pour calculer les coordonnées d’un vecteur

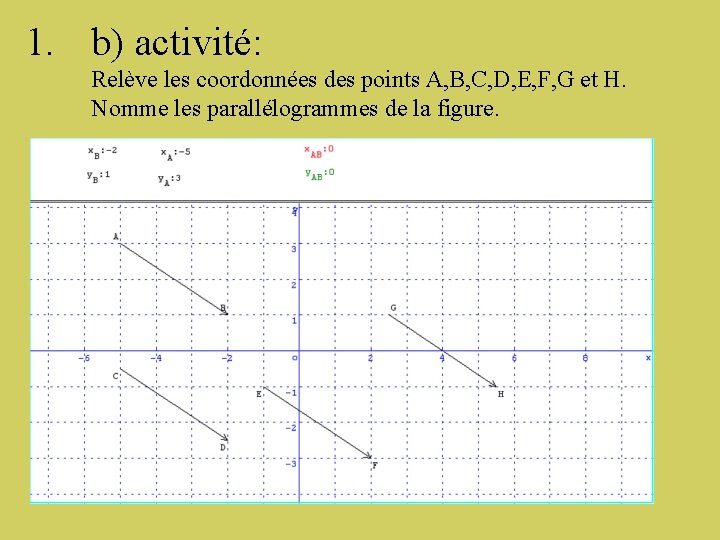
1. b) activité: Relève les coordonnées des points A, B, C, D, E, F, G et H. Nomme les parallélogrammes de la figure.

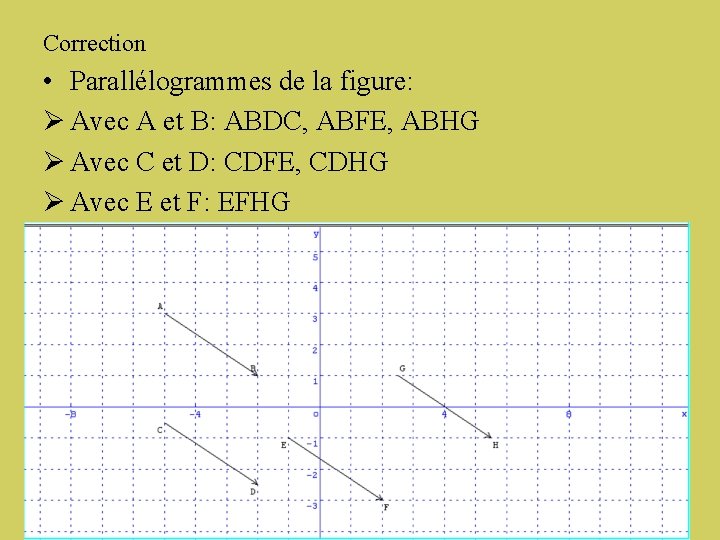
Correction • Parallélogrammes de la figure: Ø Avec A et B: ABDC, ABFE, ABHG Ø Avec C et D: CDFE, CDHG Ø Avec E et F: EFHG

Points A B C D E F abscisse -5 -2 -1 2 2, 5 5, 5 ordonnée 3 1 -0, 5 -2, 5 -1 -3 G 1 H -1

b) Bilan: Admettons et retenons:

III. Applications

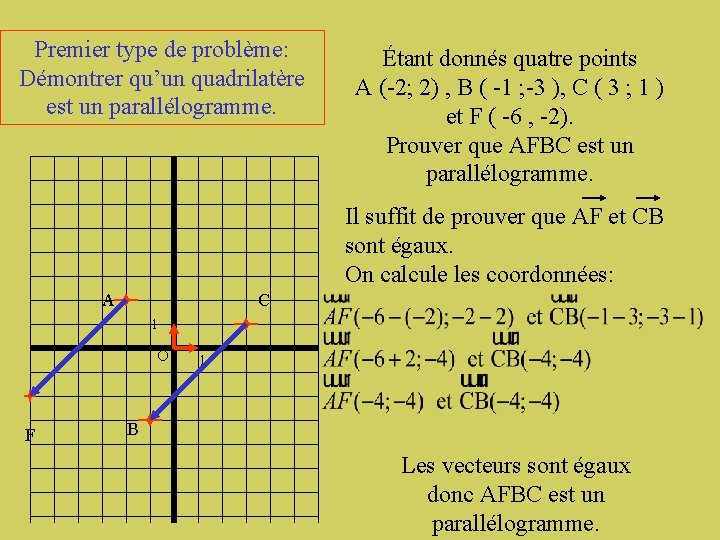
Premier type de problème: Démontrer qu’un quadrilatère est un parallélogramme. Étant donnés quatre points A (-2; 2) , B ( -1 ; -3 ), C ( 3 ; 1 ) et F ( -6 , -2). Prouver que AFBC est un parallélogramme. Il suffit de prouver que AF et CB sont égaux. On calcule les coordonnées: A C 1 O F 1 B Les vecteurs sont égaux donc AFBC est un parallélogramme.

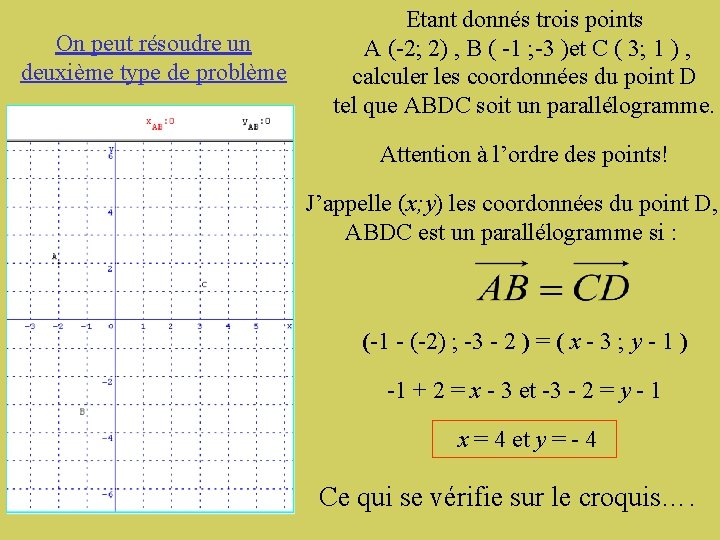
On peut résoudre un deuxième type de problème Etant donnés trois points A (-2; 2) , B ( -1 ; -3 )et C ( 3; 1 ) , calculer les coordonnées du point D tel que ABDC soit un parallélogramme. Attention à l’ordre des points! J’appelle (x; y) les coordonnées du point D, ABDC est un parallélogramme si : (-1 - (-2) ; -3 - 2 ) = ( x - 3 ; y - 1 ) -1 + 2 = x - 3 et -3 - 2 = y - 1 x = 4 et y = - 4 Ce qui se vérifie sur le croquis….

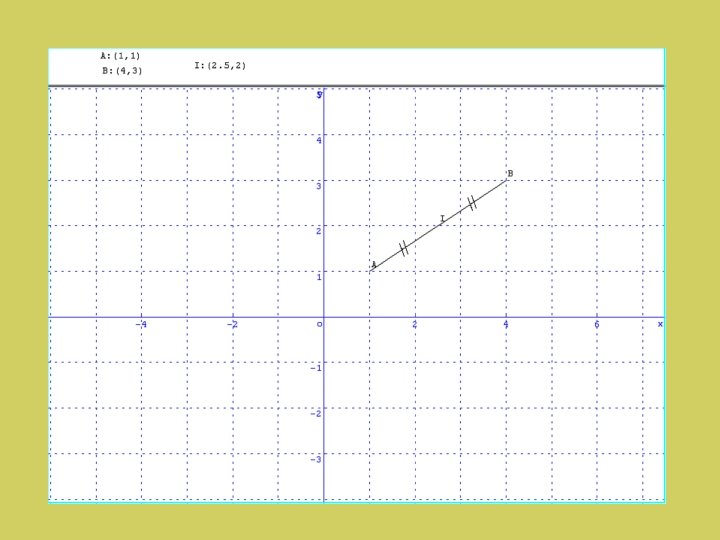
IV. Coordonnées du milieu d’un segment

Démonstration

A retenir Les coordonnées du milieu d'un segment [AB] sont données par la formule

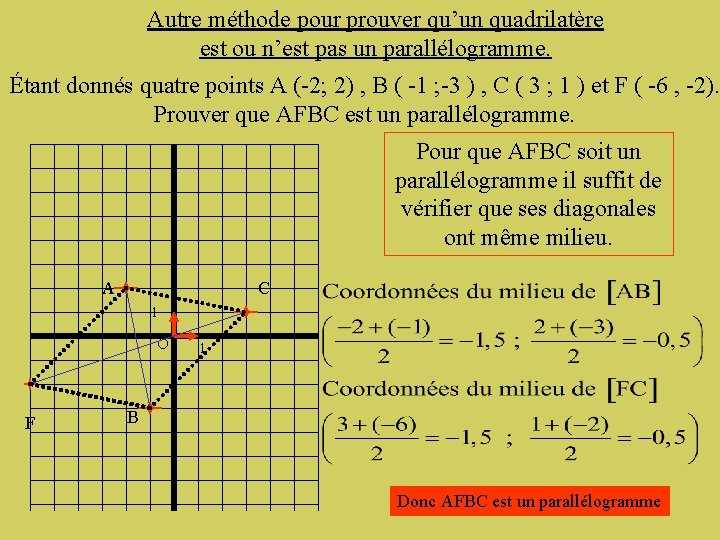
Autre méthode pour prouver qu’un quadrilatère est ou n’est pas un parallélogramme. Étant donnés quatre points A (-2; 2) , B ( -1 ; -3 ) , C ( 3 ; 1 ) et F ( -6 , -2). Prouver que AFBC est un parallélogramme. Pour que AFBC soit un parallélogramme il suffit de vérifier que ses diagonales ont même milieu. A C 1 O F 1 B Donc AFBC est un parallélogramme

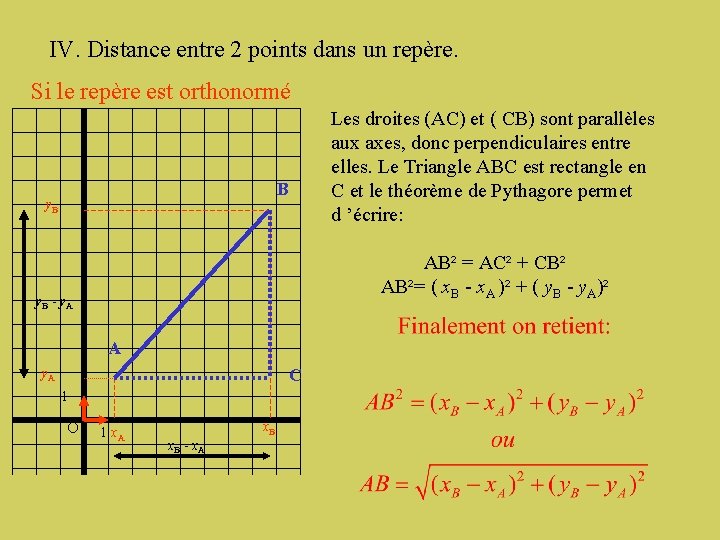
IV. Distance entre 2 points dans un repère. Si le repère est orthonormé Les droites (AC) et ( CB) sont parallèles aux axes, donc perpendiculaires entre elles. Le Triangle ABC est rectangle en C et le théorème de Pythagore permet d ’écrire: B y. B AB² = AC² + CB² AB²= ( x. B - x. A )² + ( y. B - y. A)² y. B - y. A A C y. A 1 O 1 x. A x. B - x. A