Chapitre 1 le diagramme de Bode Ce diagramme

Chapitre 1 le diagramme de Bode Ce diagramme représente les performance d’un système électrique, mécanique, thermique 1

L’analyse fréquentielle d’un quadripôle se fait en régime sinusoïdal pur, essentiellement avec le calcul complexe. 1. La fonction de transfert T (jw) d’un quadripôle est le rapport Retenir aussi que Vs = T(jw). Ve. Elle est aussi appelée transmittance complexe, transmittance isochrone ou amplification. Elle n’a pas d’unité. Son module est le rapport des valeurs efficaces | T (jw) | = T = Si T = = 5 signifie que Vs = 5 Ve. Si T > 1 le quadripôle amplifie alors que si T < 1 le quadripôle atténue Son argument est le déphasage de la tension de sortie vs par rapport à la tension d’entrée ve. En effet, arg = arg Vs - arg Ve = js - je = j 2

2. Le diagramme de Bode est la représentation du gain Gd. B = 20 log | T(jw) | et de l’argument j = arg T(jw) en fonction de la fréquence f ou w = 2 pf en échelle logarithmique. log est la fonction logarithme décimal a) Le gain d’un quadripôle est la valeur Gd. B = 20 log |T (jw)| = 20 log T. « log » est le logarithme décimal, c’est la fonction inverse de « 10 x » : 100 = 1 donc log 1 = 0 ; 101 = 10 donc log 10 = 1 ; 102 = 100 donc log 102 = 2 ; log 103 = 3 ; etc. … Si T = 1 (montage suiveur) Gd. B = 20 log 1 = 0 d. B, si T = 10, Gd. B = 20 log 10 = 20 d. B, si T = 100, Gd. B = 20 log 100 = 40 d. B, si T = 100 000, Gd. B = 20 log 105 = 100 d. B, si T = 0, 1, Gd. B = 20 log 10 -1 = - 20 d. B, si T = 0, 01, Gd. B = 20 log 10 -2 = -40 d. B, etc. … 3

S’il y a amplification, Gd. B > 0 d. B, alors que s’il y a atténuation, Gd. B < 0 d. B. La relation inverse : Gd. B = 20 log T = T = 10 ^ ( ^ = à la puissance) exemple : 14 d. B correspond à une amplification de 10^(14/20) = 5 4

5

b) l’échelle logarithmique : f sur l’échelle logarithmique est placé à log f sur l’échelle linéaire la décade est l’intervalle de fréquence entre f et 10 f log 10. f = log 10 + log f = 1 + log f donc entre f et 10 f il y a 1 unité de longueur (ici 5 cm). l’octave est l’intervalle de fréquence entre f et 2 f log 2. f = log 2 + log f = 0, 3 + log f donc entre f et 10 f il y a un module. En musique, il y a huit degrés dans une gamme. L’octave est constituée des huit notes suivantes : do(1), ré, mi, fa, sol, la, si et do(8). La fréquence de do(8) est le double de celle de do(1). , Sur l’axe gradué représenté ci-dessus, il y a 3 modules. 6

c) intérêt des diagrammes de Bode a On utilise les propriétés mathématiques de la fonction logarithme qui transforme une multiplication en addition : log (Ax. B) = log A + log B. Pour les arguments des nombres complexes, c’est pareil : arg (A. B) = arg A + arg B D’où la règle pour réaliser facilement des diagrammes de Bode : la représentation du gain s’obtient en faisant la somme des représentations des gains Gd. B = Gd. B 1 + Gd. B 2 + Gd. B 3 + … + Gd. Bn et la représentation de la phase s’obtient en faisant la somme des représentations des phases j = j 1 + j 2 + j 3 + … + jn. 7

8

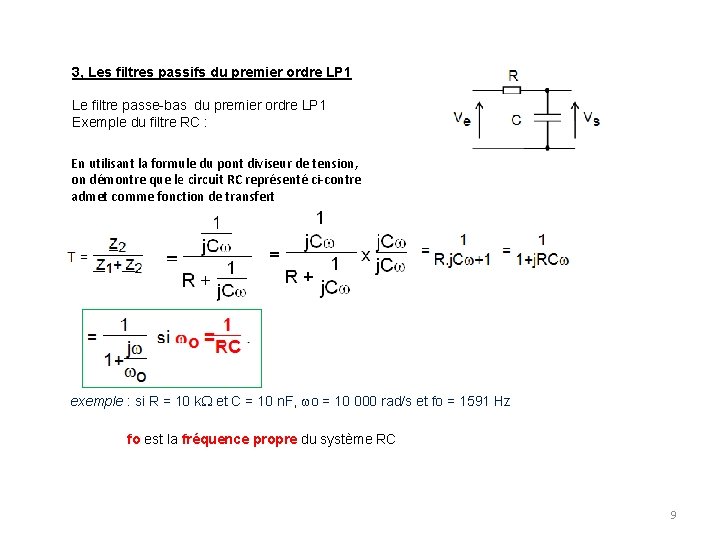
3, Les filtres passifs du premier ordre LP 1 Le filtre passe-bas du premier ordre LP 1 Exemple du filtre RC : En utilisant la formule du pont diviseur de tension, on démontre que le circuit RC représenté ci-contre admet comme fonction de transfert exemple : si R = 10 k. W et C = 10 n. F, wo = 10 000 rad/s et fo = 1591 Hz fo est la fréquence propre du système RC 9

Lorsque w << wo , T ( jw ) = 1 donc Gd. B = 20 log 1 = 0 d. B. La phase vaut 0°. La représentation de Bode du système passe bas Lorsque w >> wo , Gd. B = f(f) est une droite de pente - 20 d. B / décade. La phase vaut - 90°. Lorsque w = wo La représentation asymptotique de T ( jw ) diffère de la courbe réelle autour de w = wo. Gd. B = - 20 log |1 + j | = - 20 log = - 20 log= - 3 d. B fo est aussi appelé fc la fréquence de coupure à -3 d. B. La phase pour w = wo vaut arg T(j) = - 45° 10

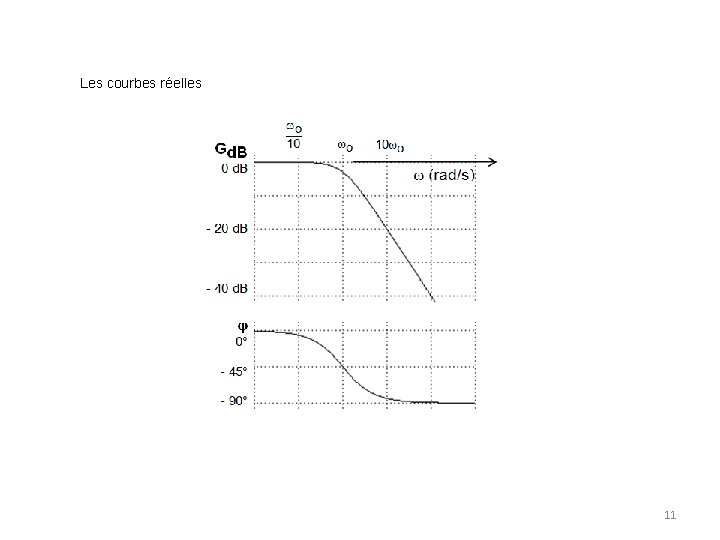
Les courbes réelles 11

12

4. Les systèmes du deuxième ordre Exemple d’un système passe-bas du deuxième ordre a) la fonction de transfert T (jw) = C’est la forme canonique d’un filtre passe-bas du deuxième ordre, LP 2 en anglais (“low pass”), où m est le coefficient d’amortissement et wo est la pulsation propre. Pour le circuit RLC ci-dessus 13

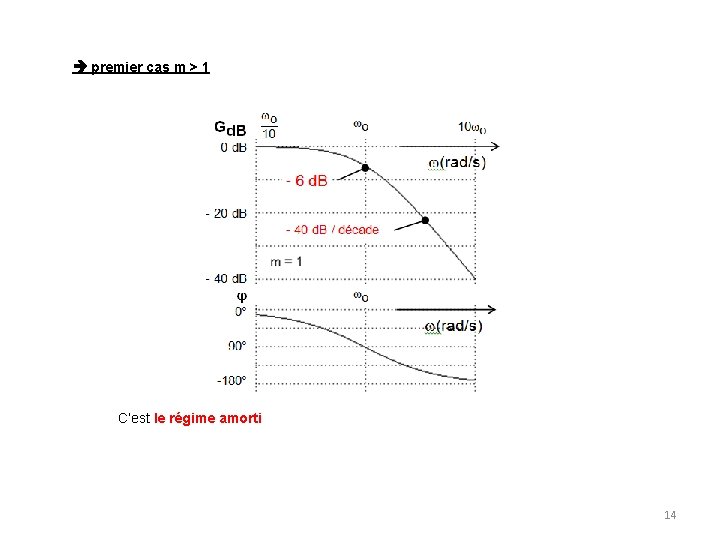
premier cas m > 1 C’est le régime amorti 14

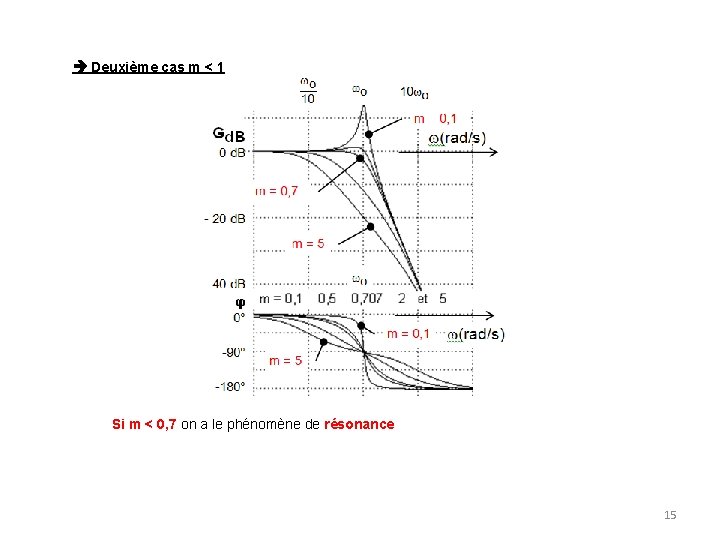
Deuxième cas m < 1 Si m < 0, 7 on a le phénomène de résonance 15

5, Les autres filtres Le filtre passe-haut HP Le filtre passe-bande BP Le filtre réjecteur de bande NF (notch filter) Le filtre passe-tout (AP pour all pass) est un circuit déphaseur 16

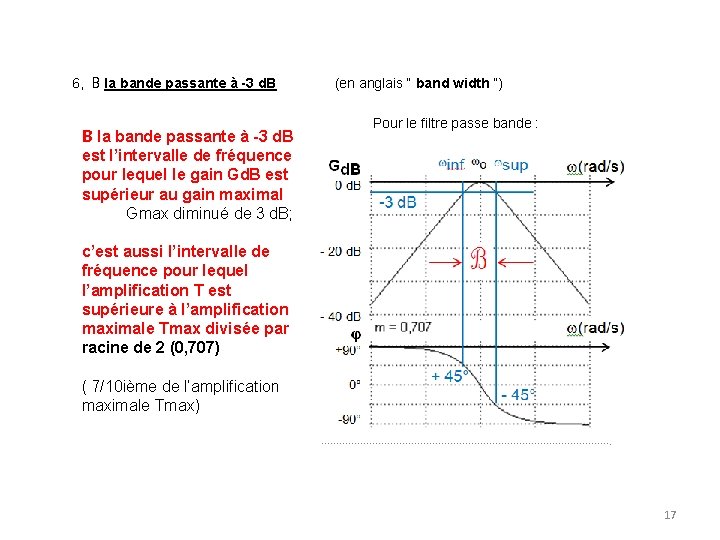
6, B la bande passante à -3 d. B (en anglais “ band width ”) B la bande passante à -3 d. B est l’intervalle de fréquence pour lequel le gain Gd. B est supérieur au gain maximal Gmax diminué de 3 d. B; Pour le filtre passe bande : c’est aussi l’intervalle de fréquence pour lequel l’amplification T est supérieure à l’amplification maximale Tmax divisée par racine de 2 (0, 707) ( 7/10 ième de l’amplification maximale Tmax) 17

Fin du chapitre 18