Chaper 12 Indexing Database System Concepts 5 th

Chaper 12: Indexing Database System Concepts, 5 th Ed. ©Silberschatz, Korth and Sudarshan See www. db-book. com for conditions on re-use

Basic Concepts n Indexing mechanisms used to speed up access to desired data. l E. g. , author catalog in library n Search Key - attribute to set of attributes used to look up records in a file. n An index file consists of records (called index entries) of the form search-key pointer n Index files are typically much smaller than the original file n Two basic kinds of indices: l Ordered indices: search keys are stored in sorted order l Hash indices: search keys are distributed uniformly across “buckets” using a “hash function”. Database System Concepts - 5 th Edition. 12. 2 ©Silberschatz, Korth and Sudarshan

Index Evaluation Metrics n Access types supported efficiently. E. g. , l records with a specified value in the attribute l or records with an attribute value falling in a specified range of values. n Access time n Insertion time n Deletion time n Space overhead Database System Concepts - 5 th Edition. 12. 3 ©Silberschatz, Korth and Sudarshan

Ordered Indices n In an ordered index, index entries are stored sorted on the search key value. E. g. , author catalog in library. n Primary index: in a sequentially ordered file, the index whose search key specifies the sequential order of the file. l Also called clustering index l The search key of a primary index is usually but not necessarily the primary key. n Secondary index: an index whose search key specifies an order different from the sequential order of the file. Also called non-clustering index. n Index-sequential file: ordered sequential file with a primary index. Database System Concepts - 5 th Edition. 12. 4 ©Silberschatz, Korth and Sudarshan

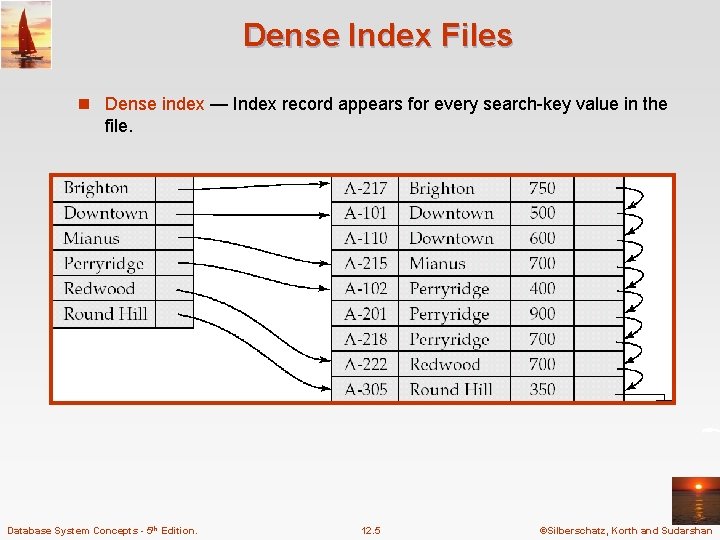
Dense Index Files n Dense index — Index record appears for every search-key value in the file. Database System Concepts - 5 th Edition. 12. 5 ©Silberschatz, Korth and Sudarshan

Sparse Index Files n Sparse Index: contains index records for only some search-key values. l Applicable when records are sequentially ordered on search-key n To locate a record with search-key value K we: l Find index record with largest search-key value < K l Search file sequentially starting at the record to which the index record points Database System Concepts - 5 th Edition. 12. 6 ©Silberschatz, Korth and Sudarshan

Sparse Index Files (Cont. ) n Compared to dense indices: l Less space and less maintenance overhead for insertions and deletions. l Generally slower than dense index for locating records. n Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block. Database System Concepts - 5 th Edition. 12. 7 ©Silberschatz, Korth and Sudarshan

Multilevel Index n If primary index does not fit in memory, access becomes expensive. n Solution: treat primary index kept on disk as a sequential file and construct a sparse index on it. l outer index – a sparse index of primary index l inner index – the primary index file n If even outer index is too large to fit in main memory, yet another level of index can be created, and so on. n Indices at all levels must be updated on insertion or deletion from the file. Database System Concepts - 5 th Edition. 12. 8 ©Silberschatz, Korth and Sudarshan

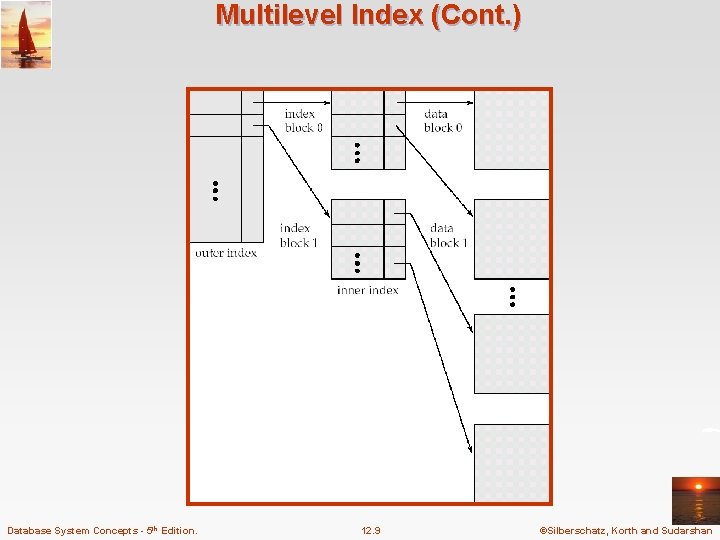
Multilevel Index (Cont. ) Database System Concepts - 5 th Edition. 12. 9 ©Silberschatz, Korth and Sudarshan

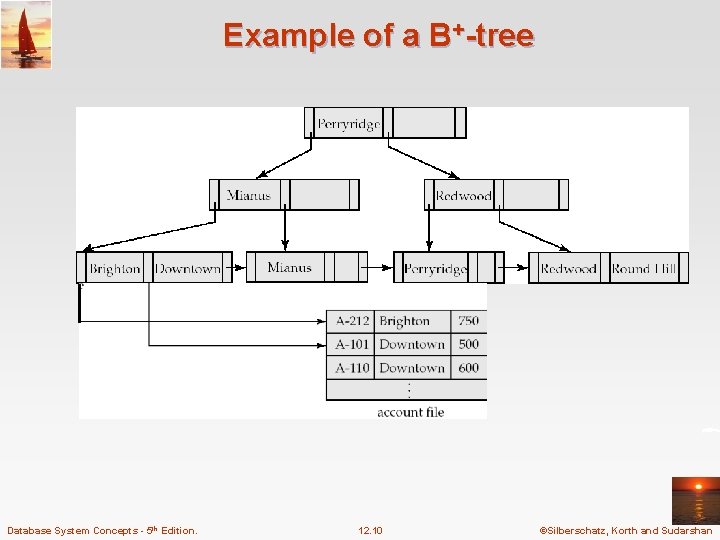
Example of a B+-tree for account file (n = 3) Database System Concepts - 5 th Edition. 12. 10 ©Silberschatz, Korth and Sudarshan

B+-Tree Index Files A B+-tree is a rooted tree satisfying the following properties: n All paths from root to leaf are of the same length n Each node that is not a root or a leaf has between n/2 and n children. n A leaf node has between (n– 1)/2 and n– 1 values n Special cases: l If the root is not a leaf, it has at least 2 children. l If the root is a leaf (that is, there are no other nodes in the tree), it can have between 0 and (n– 1) values. Database System Concepts - 5 th Edition. 12. 11 ©Silberschatz, Korth and Sudarshan

B+-Tree Node Structure n Typical node l Ki are the search-key values l Pi are pointers to children (for non-leaf nodes) or pointers to records or buckets of records (for leaf nodes). n The search-keys in a node are ordered K 1 < K 2 < K 3 <. . . < Kn– 1 Database System Concepts - 5 th Edition. 12. 12 ©Silberschatz, Korth and Sudarshan

Leaf Nodes in B+-Trees Properties of a leaf node: n For i = 1, 2, . . . , n– 1, pointer Pi either points to a file record with search- key value Ki, or to a bucket of pointers to file records, each record having search-key value Ki. Only need bucket structure if search-key does not form a primary key. n If Li, Lj are leaf nodes and i < j, Li’s search-key values are less than Lj’s search-key values n Pn points to next leaf node in search-key order Database System Concepts - 5 th Edition. 12. 13 ©Silberschatz, Korth and Sudarshan

Non-Leaf Nodes in B+-Trees n Non leaf nodes form a multi-level sparse index on the leaf nodes. For a non-leaf node with m pointers: l All the search-keys in the subtree to which P 1 points are less than K 1 l For 2 i n – 1, all the search-keys in the subtree to which Pi points have values greater than or equal to Ki– 1 and less than Km– 1 Database System Concepts - 5 th Edition. 12. 14 ©Silberschatz, Korth and Sudarshan

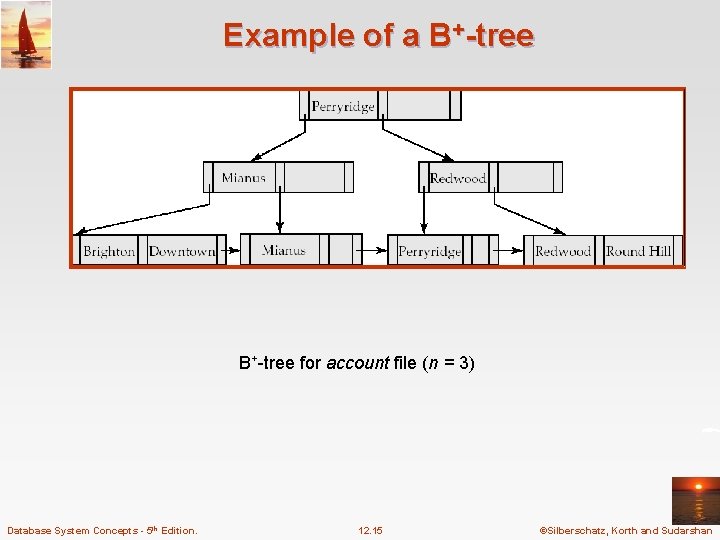
Example of a B+-tree for account file (n = 3) Database System Concepts - 5 th Edition. 12. 15 ©Silberschatz, Korth and Sudarshan

Example of B+-tree for account file (n = 5) n Leaf nodes must have between 2 and 4 values ( (n– 1)/2 and n – 1, with n = 5). n Non-leaf nodes other than root must have between 3 and 5 children ( (n/2 and n with n =5). n Root must have at least 2 children. Database System Concepts - 5 th Edition. 12. 16 ©Silberschatz, Korth and Sudarshan

Observations about B+-trees n Since the inter-node connections are done by pointers, “logically” close blocks need not be “physically” close. n The non-leaf levels of the B+-tree form a hierarchy of sparse indices. n The B+-tree contains a relatively small number of levels 4 Level 4 Next 4. . below root has at least 2* n/2 values level has at least 2* n/2 values etc. l If there are K search-key values in the file, the tree height is no more than log n/2 (K) l thus searches can be conducted efficiently. n Insertions and deletions to the main file can be handled efficiently, as the index can be restructured in logarithmic time (as we shall see). Database System Concepts - 5 th Edition. 12. 17 ©Silberschatz, Korth and Sudarshan

Queries on B+-Trees n Find all records with a search-key value of k. 1. N=root 2. Repeat 1. Examine N for the smallest search-key value > k. 2. If such a value exists, assume it is Ki. Then set N = Pi 3. Otherwise k Kn– 1. Set N = Pn Until N is a leaf node 3. If for some i, key Ki = k follow pointer Pi to the desired record or bucket. 4. Else no record with search-key value k exists. Database System Concepts - 5 th Edition. 12. 18 ©Silberschatz, Korth and Sudarshan

Queries on B+-Trees (Cont. ) n If there are K search-key values in the file, the height of the tree is no more than log n/2 (K). n A node is generally the same size as a disk block, typically 4 kilobytes l and n is typically around 100 (40 bytes per index entry). n With 1 million search key values and n = 100 l at most log 50(1, 000) = 4 nodes are accessed in a lookup. n Contrast this with a balanced binary free with 1 million search key values — around 20 nodes are accessed in a lookup l above difference is significant since every node access may need a disk I/O, costing around 20 milliseconds Database System Concepts - 5 th Edition. 12. 19 ©Silberschatz, Korth and Sudarshan

Updates on B+-Trees: Insertion 1. Find the leaf node in which the search-key value would appear 2. If the search-key value is already present in the leaf node 1. Add record to the file 2. If necessary add a pointer to the bucket. 3. If the search-key value is not present, then 1. add the record to the main file (and create a bucket if necessary) 2. If there is room in the leaf node, insert (key-value, pointer) pair in the leaf node 3. Otherwise, split the node (along with the new (key-value, pointer) entry) as discussed in the next slide. Database System Concepts - 5 th Edition. 12. 20 ©Silberschatz, Korth and Sudarshan

Updates on B+-Trees: Insertion (Cont. ) n Splitting a leaf node: l take the n (search-key value, pointer) pairs (including the one being inserted) in sorted order. Place the first n/2 in the original node, and the rest in a new node. l let the new node be p, and let k be the least key value in p. Insert (k, p) in the parent of the node being split. l If the parent is full, split it and propagate the split further up. n Splitting of nodes proceeds upwards till a node that is not full is found. l In the worst case the root node may be split increasing the height of the tree by 1. Result of splitting node containing Brighton and Downtown on inserting Clearview Next step: insert entry with (Downtown, pointer-to-new-node) into parent Database System Concepts - 5 th Edition. 12. 21 ©Silberschatz, Korth and Sudarshan

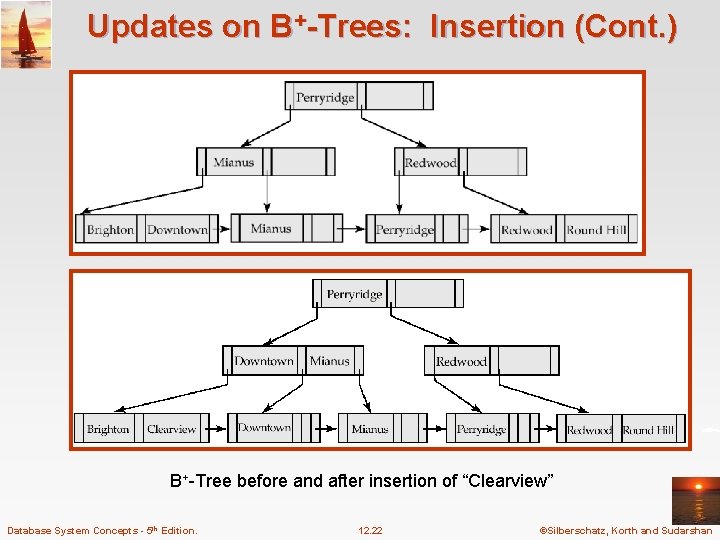
Updates on B+-Trees: Insertion (Cont. ) B+-Tree before and after insertion of “Clearview” Database System Concepts - 5 th Edition. 12. 22 ©Silberschatz, Korth and Sudarshan

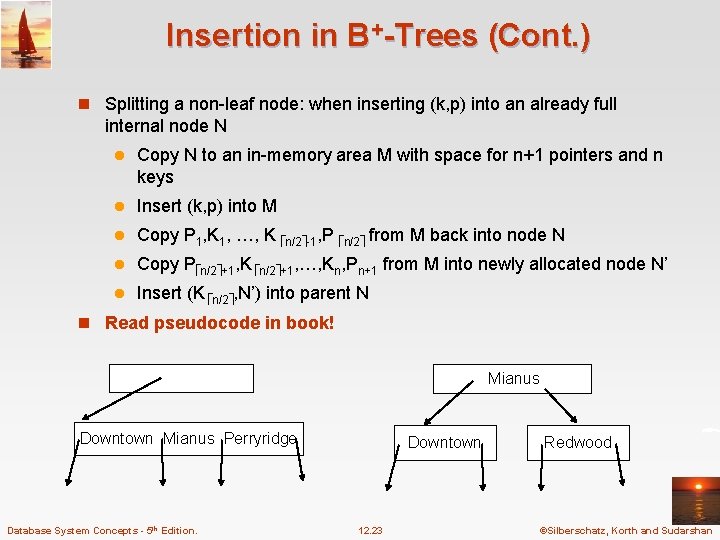
Insertion in B+-Trees (Cont. ) n Splitting a non-leaf node: when inserting (k, p) into an already full internal node N l Copy N to an in-memory area M with space for n+1 pointers and n keys l Insert (k, p) into M l Copy P 1, K 1, …, K n/2 -1, P n/2 from M back into node N l Copy P n/2 +1, K n/2 +1, …, Kn, Pn+1 from M into newly allocated node N’ l Insert (K n/2 , N’) into parent N n Read pseudocode in book! Mianus Downtown Mianus Perryridge Database System Concepts - 5 th Edition. Downtown 12. 23 Redwood ©Silberschatz, Korth and Sudarshan

Updates on B+-Trees: Deletion n Find the record to be deleted, and remove it from the main file and from the bucket (if present) n Remove (search-key value, pointer) from the leaf node if there is no bucket or if the bucket has become empty n If the node has too few entries due to the removal, and the entries in the node and a sibling fit into a single node, then merge siblings: l Insert all the search-key values in the two nodes into a single node (the on the left), and delete the other node. l Delete the pair (Ki– 1, Pi), where Pi is the pointer to the deleted node, from its parent, recursively using the above procedure. Database System Concepts - 5 th Edition. 12. 24 ©Silberschatz, Korth and Sudarshan

Updates on B+-Trees: Deletion n Otherwise, if the node has too few entries due to the removal, but the entries in the node and a sibling do not fit into a single node, then redistribute pointers: l Redistribute the pointers between the node and a sibling such that both have more than the minimum number of entries. l Update the corresponding search-key value in the parent of the node. n The node deletions may cascade upwards till a node which has n/2 or more pointers is found. n If the root node has only one pointer after deletion, it is deleted and the sole child becomes the root. Database System Concepts - 5 th Edition. 12. 25 ©Silberschatz, Korth and Sudarshan

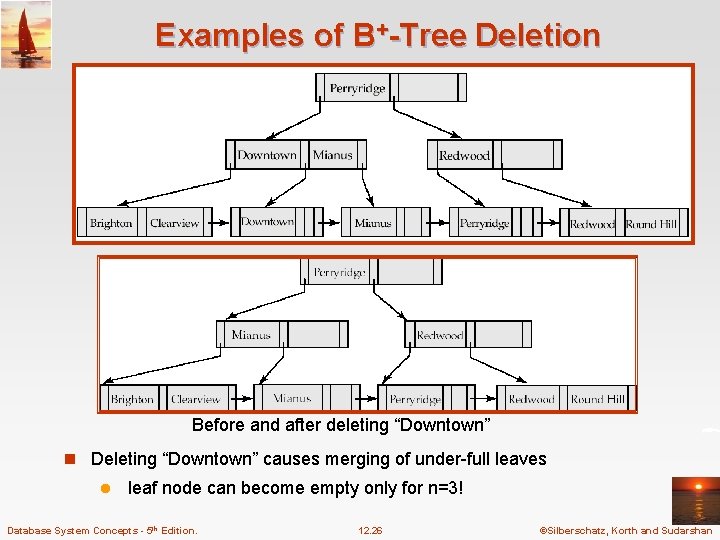
Examples of B+-Tree Deletion Before and after deleting “Downtown” n Deleting “Downtown” causes merging of under-full leaves l leaf node can become empty only for n=3! Database System Concepts - 5 th Edition. 12. 26 ©Silberschatz, Korth and Sudarshan

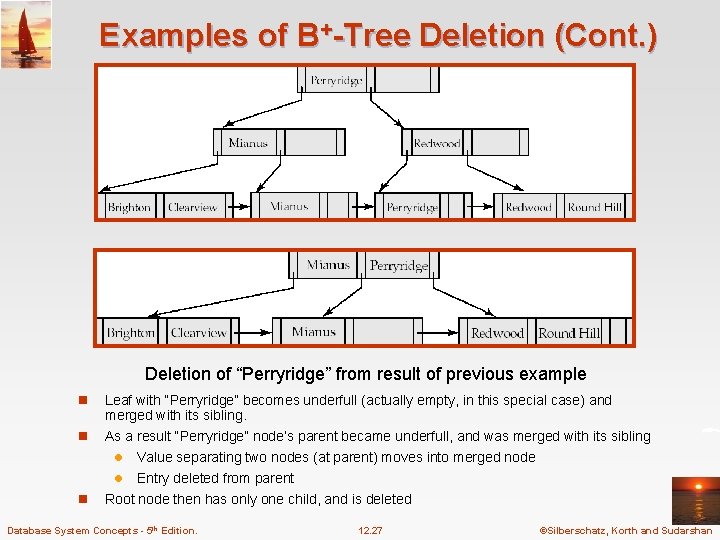
Examples of B+-Tree Deletion (Cont. ) Deletion of “Perryridge” from result of previous example n n n Leaf with “Perryridge” becomes underfull (actually empty, in this special case) and merged with its sibling. As a result “Perryridge” node’s parent became underfull, and was merged with its sibling l Value separating two nodes (at parent) moves into merged node l Entry deleted from parent Root node then has only one child, and is deleted Database System Concepts - 5 th Edition. 12. 27 ©Silberschatz, Korth and Sudarshan

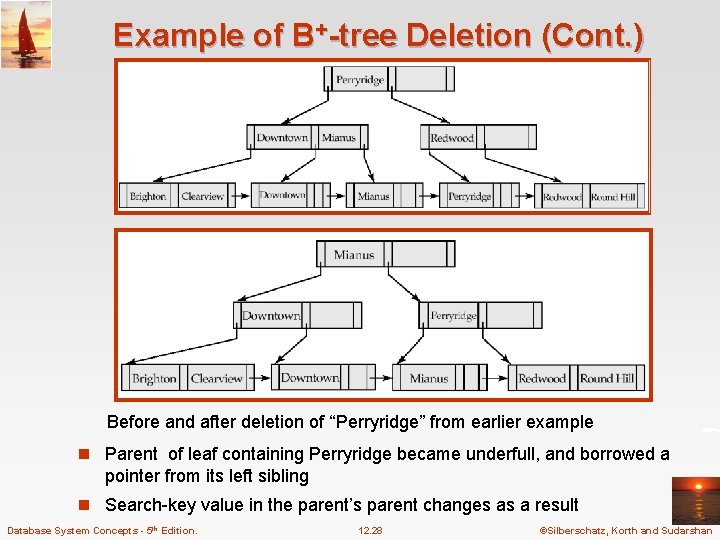
Example of B+-tree Deletion (Cont. ) Before and after deletion of “Perryridge” from earlier example n Parent of leaf containing Perryridge became underfull, and borrowed a pointer from its left sibling n Search-key value in the parent’s parent changes as a result Database System Concepts - 5 th Edition. 12. 28 ©Silberschatz, Korth and Sudarshan

Multiple-Key Access n Use multiple indices for certain types of queries. n Example: select account_number from account where branch_name = “Perryridge” and balance = 1000 n Possible strategies for processing query using indices on single attributes: 1. Use index on branch_name to find accounts with balances of $1000; test branch_name = “Perryridge”. 2. Use index on balance to find accounts with balances of $1000; test branch_name = “Perryridge”. 3. Use branch_name index to find pointers to all records pertaining to the Perryridge branch. Similarly use index on balance. Take intersection of both sets of pointers obtained. Database System Concepts - 5 th Edition. 12. 29 ©Silberschatz, Korth and Sudarshan

Indices on Multiple Keys n Composite search keys are search keys containing more than one attribute l E. g. (branch_name, balance) n Lexicographic ordering: (a 1, a 2) < (b 1, b 2) if either l a 1 < b 1, or l a 1=b 1 and a 2 < b 2 Database System Concepts - 5 th Edition. 12. 30 ©Silberschatz, Korth and Sudarshan

Indices on Multiple Attributes Suppose we have an index on combined search-key (branch_name, balance). n With the where clause where branch_name = “Perryridge” and balance = 1000 the index on (branch_name, balance) can be used to fetch only records that satisfy both conditions. l Using separate indices in less efficient — we may fetch many records (or pointers) that satisfy only one of the conditions. n Can also efficiently handle where branch_name = “Perryridge” and balance < 1000 n But cannot efficiently handle where branch_name < “Perryridge” and balance = 1000 l May fetch many records that satisfy the first but not the secondition Database System Concepts - 5 th Edition. 12. 31 ©Silberschatz, Korth and Sudarshan

Bitmap Indices n Bitmap indices are a special type of index designed for efficient querying on multiple keys n Records in a relation are assumed to be numbered sequentially from, say, 0 l Given a number n it must be easy to retrieve record n 4 Particularly easy if records are of fixed size n Applicable on attributes that take on a relatively small number of distinct values l E. g. gender, country, state, … l E. g. income-level (income broken up into a small number of levels such as 0 -9999, 10000 -19999, 20000 -50000, 50000 - infinity) n A bitmap is simply an array of bits Database System Concepts - 5 th Edition. 12. 32 ©Silberschatz, Korth and Sudarshan

Bitmap Indices (Cont. ) n In its simplest form a bitmap index on an attribute has a bitmap for each value of the attribute l Bitmap has as many bits as records l In a bitmap for value v, the bit for a record is 1 if the record has the value v for the attribute, and is 0 otherwise Database System Concepts - 5 th Edition. 12. 33 ©Silberschatz, Korth and Sudarshan

Bitmap Indices (Cont. ) n Bitmap indices are useful for queries on multiple attributes l n n not particularly useful for single attribute queries Queries are answered using bitmap operations l Intersection (and) l Union (or) l Complementation (not) Each operation takes two bitmaps of the same size and applies the operation on corresponding bits to get the result bitmap l E. g. 100110 AND 110011 = 100010 100110 OR 110011 = 110111 NOT 100110 = 011001 l Males with income level L 1: 10010 AND 10100 = 10000 4 Can then retrieve required tuples. 4 Counting number of matching tuples is even faster Database System Concepts - 5 th Edition. 12. 34 ©Silberschatz, Korth and Sudarshan

Bitmap Indices (Cont. ) n Bitmap indices generally very small compared with relation size l E. g. if record is 100 bytes, space for a single bitmap is 1/800 of space used by relation. 4 If number of distinct attribute values is 8, bitmap is only 1% of relation size n Deletion needs to be handled properly l Existence bitmap to note if there is a valid record at a record location l Needed for complementation 4 not(A=v): (NOT bitmap-A-v) AND Existence. Bitmap n Should keep bitmaps for all values, even null value l To correctly handle SQL null semantics for NOT(A=v): 4 intersect above result with (NOT bitmap-A-Null) Database System Concepts - 5 th Edition. 12. 35 ©Silberschatz, Korth and Sudarshan

Efficient Implementation of Bitmap Operations n Bitmaps are packed into words; a single word and (a basic CPU instruction) computes and of 32 or 64 bits at once l E. g. 1 -million-bit maps can be and-ed with just 31, 250 instruction n Counting number of 1 s can be done fast by a trick: l Use each byte to index into a precomputed array of 256 elements each storing the count of 1 s in the binary representation 4 Can use pairs of bytes to speed up further at a higher memory cost l Add up the retrieved counts n Bitmaps can be used instead of Tuple-ID lists at leaf levels of B+-trees, for values that have a large number of matching records l l Worthwhile if > 1/64 of the records have that value, assuming a tuple-id is 64 bits Above technique merges benefits of bitmap and B+-tree indices Database System Concepts - 5 th Edition. 12. 36 ©Silberschatz, Korth and Sudarshan

Index Definition in SQL n Create an index create index <index-name> on <relation-name> (<attribute-list>) E. g. : create index b-index on branch(branch_name) n Use create unique index to indirectly specify and enforce the condition that the search key is a candidate key. l Not really required if SQL unique integrity constraint is supported n To drop an index drop index <index-name> n Most database systems allow specification of type of index, and clustering. Database System Concepts - 5 th Edition. 12. 37 ©Silberschatz, Korth and Sudarshan