Chap 5 Identical Particles 1 TwoParticle Systems 2










































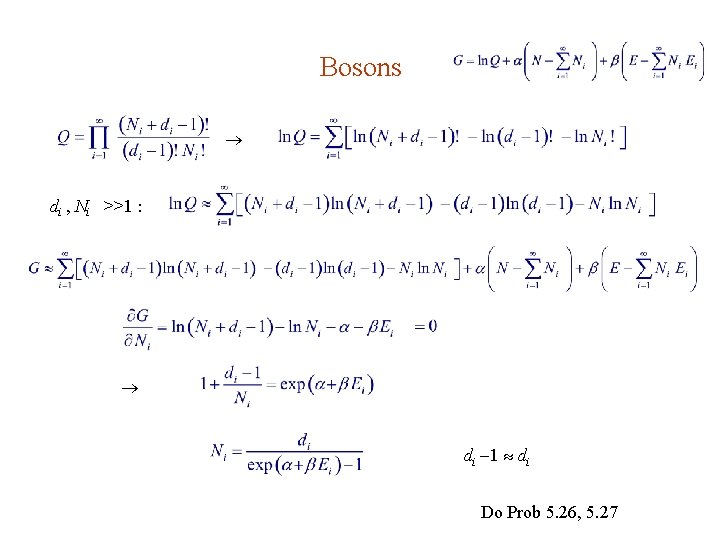





- Slides: 57

Chap 5. Identical Particles 1. Two-Particle Systems 2. Atoms 3. Solids 4. Quantum Statistical Mechanics

Two particles having the same physical attributes are equivalent. They behave the same way if subjected to the same treatment. CM: Equivalent particles are distinguishable since one can keep track of each particle all the time. QM: Equivalent particles are indistinguishable since one cannot keep track of each particle all the time due to the uncertainty principle. Indistinguishable particle are called identical.

5. 1. Two-Particle Systems 2 -particle state : Schrodinger eq. : Probability of finding particle 1 & 2 within d 3 r 1 & d 3 r 2 around r 1 & r 2 , resp. Normalization : Read Prob 5. 1, Do Prob 5. 3.

5. 1. 1. Bosons & Fermions Distinguishable particles 1 & 2 in states a & b, resp. : 1 & 2 indistinguishable (identical) : bosons fermions Spin statistics theorem : Integer spin bosons Total : Symmetric Half-integer spin fermions Anti-symm No two fermions can occupy the same state. Pauli exclusion principle

Exchange Operator Exchange operator : f Let g be the eigenfunction of P with eigenvalue : For 2 identical particles, or H & P can, & MUST, share the same eigenstates. i. e. for bosons fermions Symmetrization requirement

Example 5. 1. Infinite Square Well Consider 2 noninteracting particles, both of the same mass m, inside an infinite square well of width a. 1 -particles states are for Distinguishable particles : E. g. , Ground state: 1 st excited state : Doubly degenerate.

Bosons : Ground state: 1 st excited state : Nondegenerate Fermions : Ground state:

5. 1. 2. Exchange Forces Consider 2 particles, one in state a, the other in state b. Particles distinguishable : ( p’cle 1 in a, 2 in b. ) Bosons : ( All states are normalized ) Fermions : We’ll calculate for each case the standard deviation of particle separation

Distinguishable Particles ( , a , b normalized ) Similarly,

Identical Particles a , b orthonormal Similarly,

or Bosons are closer & fermions are further apart than the distinguishable case. Note : effective attractive repulsive exchange force for bosons fermions if particles are far apart so a , b don’t overlap.

Simplified Derivation ~ ~ if

Similarly, or Bosons are closer & fermions are further apart than the distinguishable case. Note : effective attractive repulsive exchange force for bosons fermions if particles are far apart so a , b don’t overlap.

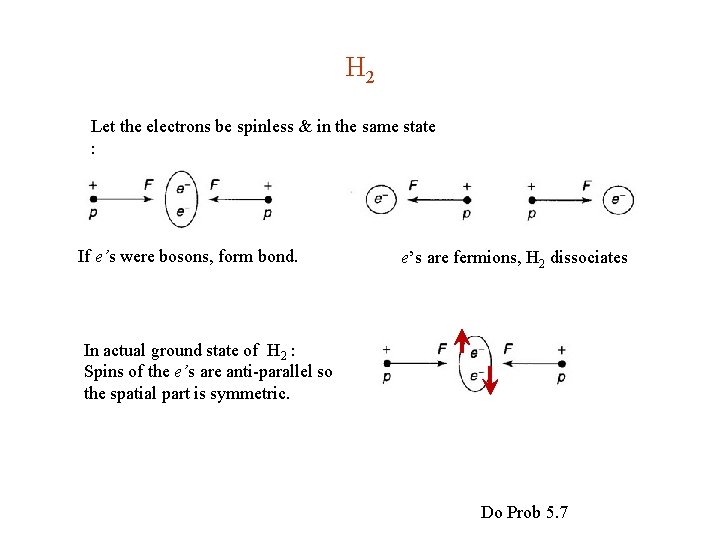
H 2 Let the electrons be spinless & in the same state : If e’s were bosons, form bond. e’s are fermions, H 2 dissociates In actual ground state of H 2 : Spins of the e’s are anti-parallel so the spatial part is symmetric. Do Prob 5. 7

5. 2. Atoms Atom with atomic number Z ( Z protons & Z electrons ) : Nucleonic Do. F dropped. See footnote, p. 211. 1 -e plan of attack : 1. Replace e-e interaction term with single particle potential. 2. Solve the 1 -e eigen-problem. 3. Contruct totally anti-symmetric Z-e wave function, including spins. 4. Total energy is just the sum of the 1 -e energies.

Non-Interaction e Model Drop all e-e terms : where ( Hydrogenic hamiltonian ) Thus where nlm and En are obtained from the hydrogen case by setting e 2 Ze 2. In particular : and (Unsymmetrized) solutions to with a 0 = Bohr radius are

5. 2. 1. Helium Non-interacting e model : Ground state : Anti-symmetrized total wave function : 0 gives only symmetric spatial part spin part must be antisymm (singlet). Experiment : Total spin is a singlet. E 0 79 e. V.

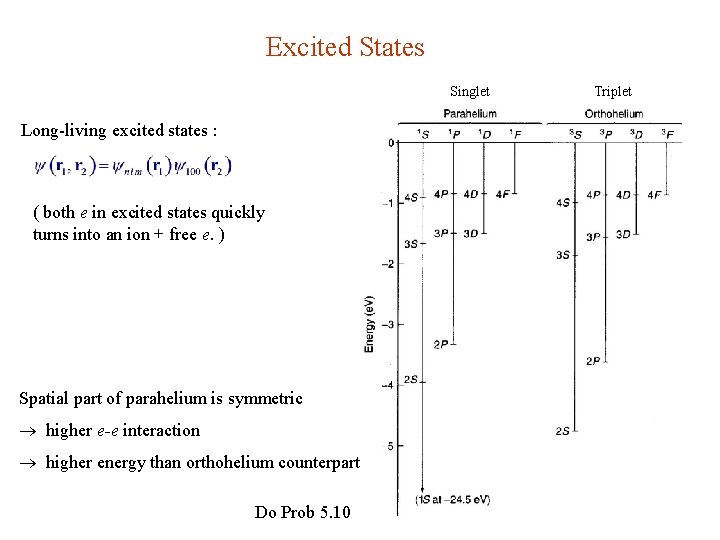
Excited States Singlet Long-living excited states : ( both e in excited states quickly turns into an ion + free e. ) Spatial part of parahelium is symmetric higher e-e interaction higher energy than orthohelium counterpart Do Prob 5. 10 Triplet

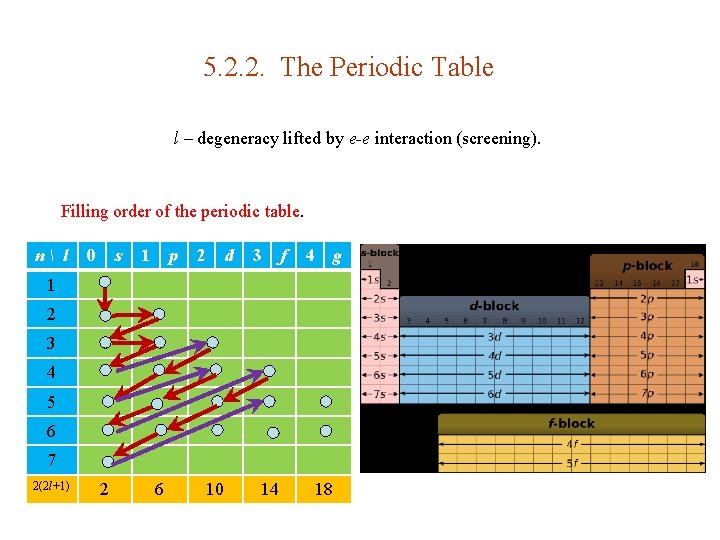
5. 2. 2. The Periodic Table l – degeneracy lifted by e-e interaction (screening). Filling order of the periodic table. n l 0 s 1 p 2 d 3 f 4 g 1 2 3 4 5 6 7 2(2 l+1) 2 6 10 14 18

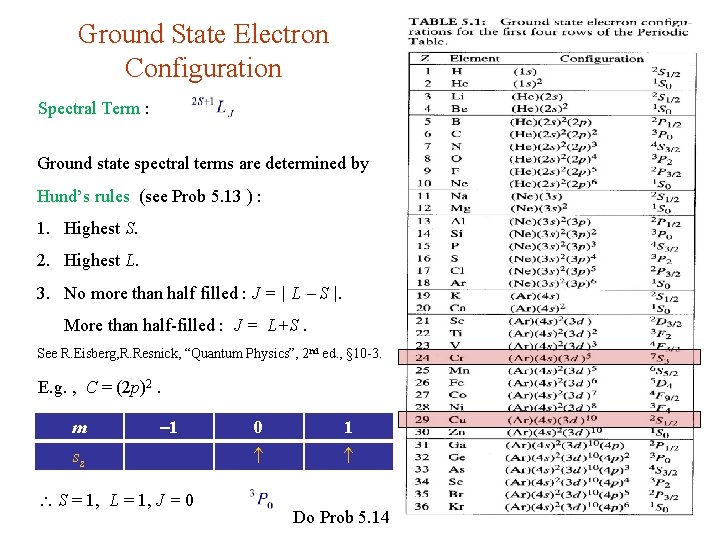
Ground State Electron Configuration Spectral Term : Ground state spectral terms are determined by Hund’s rules (see Prob 5. 13 ) : 1. Highest S. 2. Highest L. 3. No more than half filled : J = | L S |. More than half-filled : J = L+S. See R. Eisberg, R. Resnick, “Quantum Physics”, 2 nd ed. , § 10 -3. E. g. , C = (2 p)2. m 1 sz S = 1, L = 1, J = 0 0 1 Do Prob 5. 14

5. 3. Solids 1. The Free Electron Gas 2. Band Structure

5. 3. 1. The Free Electron Gas Solid modelled as a rectangular infinite well with dimensions { li , i = 1, 2, 3 }. i =1, 2, 3 unless stated otherwise for Set Let

Boundary Conditions Normalization :

k-Space Density Volume occupied by one allowed (stationary) state in the 1 st quadrant of the k-space is with ni 1. = Volume of solid k is over allowed k in 1 st quadrant of k-space. d 3 k is over all k-space. By symmetry, all 8 quadrants are equivalent. = k-space density = density of allowed states

Fermi Energy Consider a solid of N atoms, each contributing q free electrons. In the ground state, these q. N electrons will occupy the lowest q. N states. Since these states occupy a sphere centered at the origin of the k-space. Let the radius of this sphere be k. F. ( Factor 2 comes from spin degeneracy. ) = free electron density Fermi energy

Total Energy Total energy of the ground state : Compressing the solid increases its engergy. Work need be done to compress it. Electrons exerts outward pressure on the solid boundary. degeneracy pressure ( Caused by Pauli exclusion )

Miscellaneous Ideal gas : Energy per e. e gas : Do Prob 5. 16 and for Al

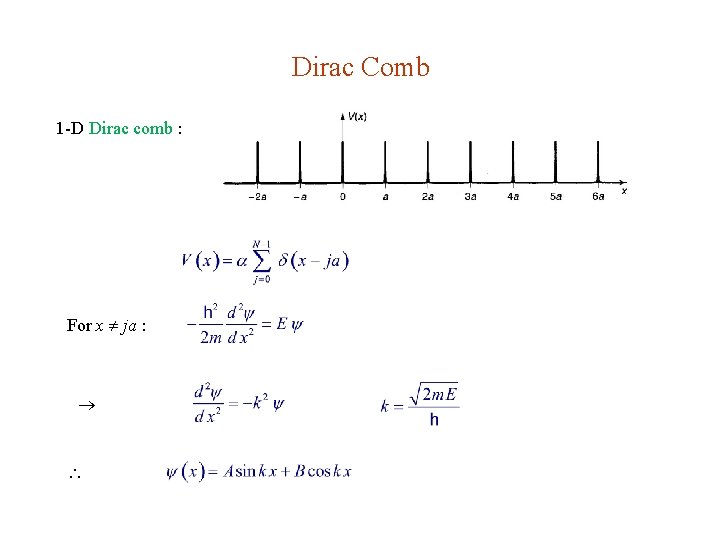
5. 3. 2. Band Structure 1 -D crystal with periodic potential For a finite solid with N atoms, strict mathematical periodicity can be achieved by imposing the periodic boundary condition Simplest model : 1 -D Dirac comb a = lattice constant

Bloch’s Theorem Bloch’s theorem : Proof : K = const Let D be the displacement operator : i. e. or D & H can share the same eigenstates. Let Since 0, setting completes the proof.

Periodic Boundary Condition For a 1 -D solid with N atoms, imposing the periodic BC gives K is real As expected

Dirac Comb 1 -D Dirac comb : For x ja :

Periodic BC x ja Impose periodic BC : Bloch’s theorem 0<x<a Let a < x < 0 continuous at x = 0

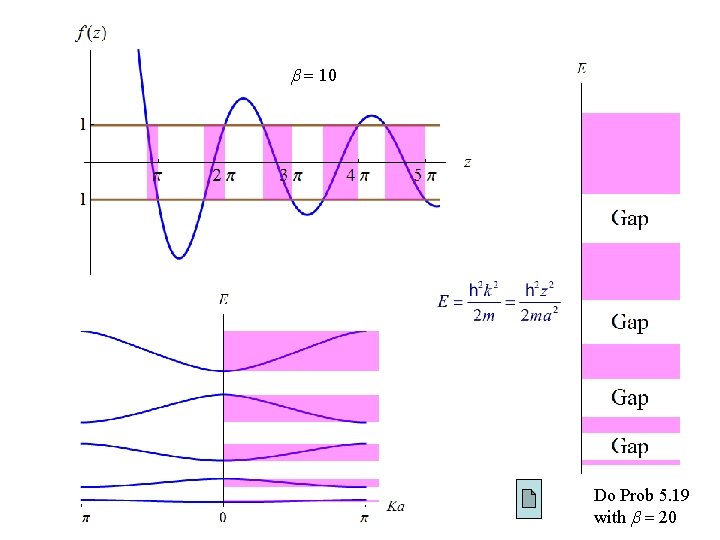
Condition for consistency is

Let Since there’s no solution for | f (z) | > 1 ( band gaps ).

10 Do Prob 5. 19 with 20

5. 4. Quantum Statistical Mechanics Fundamental assumption of statistical mechanics : In thermal equilibrium, each distinct system configuration of the same E is equally likely to occur. 1. An Example 2. The General Case 3. The Most Probable Configuration 4. Physical Significance of and 5. The Blackbody Spectrum� ( Can also be stated in terms of ensemble. )

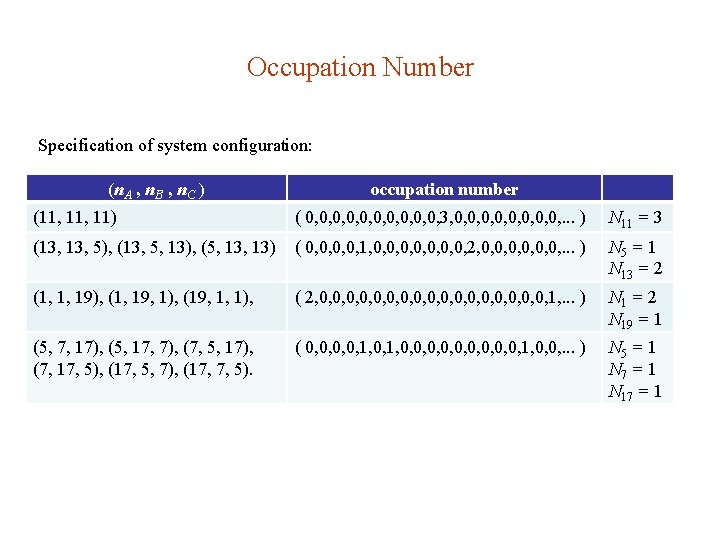
5. 4. 1. An Example Consider 3 non-interacting particles ( all of mass m ) in an 1 -D infinite square well. Let There’re 13 combinations of (n. A , n. B , n. C ) that can satisfy the condition : (11, 11), (13, 5), (13, 5, 13), (5, 13), (1, 1, 19), (1, 19, 1), (19, 1, 1), (5, 7, 17), (5, 17, 7), (7, 5, 17), (7, 17, 5), (17, 5, 7), (17, 7, 5).

Occupation Number Specification of system configuration: (n. A , n. B , n. C ) occupation number (11, 11) ( 0, 0, 0, 3, 0, 0, . . . ) N 11 = 3 (13, 5), (13, 5, 13), (5, 13) ( 0, 0, 1, 0, 0, 2, 0, 0, 0, . . . ) N 5 = 1 N 13 = 2 (1, 1, 19), (1, 19, 1), (19, 1, 1), ( 2, 0, 0, 0, 0, 0, 1, . . . ) N 1 = 2 N 19 = 1 (5, 7, 17), (5, 17, 7), (7, 5, 17), (7, 17, 5), (17, 5, 7), (17, 7, 5). ( 0, 0, 1, 0, 0, 0, 1, 0, 0, . . . ) N 5 = 1 N 7 = 1 N 17 = 1

Pn : Particles Distinguishable Particles are distinguishable each configurations is distinct. Each is equally likely when system is in equilibrium. (n. A , n. B , n. C ) Pn = Probability of finding a particle with energy En. (11, 11) (13, 5), (13, 5, 13), (5, 13) (1, 1, 19), (1, 19, 1), (19, 1, 1), (5, 7, 17), (5, 17, 7), (7, 5, 17), (7, 17, 5), (17, 5, 7), (17, 7, 5). Total = 13 distinct configurations P 1 (3/13) (2/3) = 2/13 P 5 (9/13) (1/3) = 3/13 P 7 (6/13) (1/3) = 2/13 P 11 (1/13) (3/3) = 1/13 P 13 (3/13) (2/3) = 2/13 P 17 (6/13) (1/3) = 2/13 P 19 (3/13) (1/3) = 1/13 Sum =1

Pn : Fermions occupation number ( 0, 0, 0, 3, 0, 0, . . . ) N 11 = 3 ( 0, 0, 1, 0, 0, 2, 0, 0, 0, . . . ) N 5 = 1 N 13 = 2 ( 2, 0, 0, 0, 0, 0, 1, . . . ) N 1 = 2 N 19 = 1 ( 0, 0, 1, 0, 0, 0, 1, 0, 0, . . . ) N 5 = 1 N 7 = 1 N 17 = 1 No state can be doubly occupied. Allowed distinct configurations are : 0, 0, 1, 0, 0, 0, 1, 0, 0, . . . ) Total = 1 distinct configurations Pn = Probability of finding a particle with energy En. P 1 0 P 5 (1/1) (1/3) = 1/3 P 7 (1/1) (1/3) = 1/3 P 11 0 P 13 0 N 5 = 1, N 7 = 1, N 17 = 1 P 17 (1/1) (1/3) = 1/3 P 19 0 Sum =1

Pn : Bosons occupation number ( 0, 0, 0, 3, 0, 0, . . . ) N 11 = 3 ( 0, 0, 1, 0, 0, 2, 0, 0, 0, . . . ) N 5 = 1 N 13 = 2 ( 2, 0, 0, 0, 0, 0, 1, . . . ) N 1 = 2 N 19 = 1 ( 0, 0, 1, 0, 0, 0, 1, 0, 0, . . . ) N 5 = 1 N 7 = 1 N 17 = 1 Allowed distinct configurations are : ( 0, 0, 0, 3, 0, 0, . . . ) ( 0, 0, 1, 0, 0, 2, 0, 0, 0, . . . ) ( 2, 0, 0, 0, 0, 0, 1, . . . ) ( 0, 0, 1, 0, 0, 0, 1, 0, 0, . . . ) Total = 4 distinct configurations N 11 = 3 N 5 = 1, N 13 = 2 N 1 = 2, N 19 = 1 N 5 = 1, N 7 = 1, N 17 = 1 Pn = Probability of finding a particle with energy En. P 1 (1/4) (2/3) = 1/6 P 5 (1/4) (1/3) + (1/4) (1/3) = 1/6 P 7 (1/4) (1/3) = 1/12 P 11 (1/4) (3/3) = 1/4 P 13 (1/4) (2/3) = 1/6 P 17 (1/4) (1/3) = 1/12 P 19 (1/4) (1/3) = 1/12 Sum =1

5. 4. 2. The General Case Consider a system whose 1 -particle energies are Ei with degeneracy di , i = 1, 2, 3, . . . Now, N particles are put into the system such that Ni particles have energy Ei. Question : For a given configuration (N 1 , N 2 , N 3 , . . . ), what is the number, Q(N 1 , N 2 , N 3 , . . . ), of distinct states allowed?

Distinguishable Particles Each energy level Ei corresponds to a bin with di compartments. The problem is equivalent to finding the number of distinct ways to put N particles, with Ni of them going into the di compartments of the ith bin. Ans. : 1. There’re ways, without regard of picking order, to choose N 1 particles from the whole N particles. 2. When putting a particle into the 1 st bin, there’re d 1 choices of compartments. the number of ways to put N 1 particles into the 1 st bin is 3. For the 2 nd bin, one starts with N N 1 particles so one gets

Fermions 1. Fermions are indistinguishable, so it doesn’t matter which ones are going to which bin. 2. Each bin compartment can accept atmost one fermion. So the number of way to place Ni fermions into the ith bin is if

Bosons 1. Bosons are indistinguishable, so it doesn’t matter which ones are going to which bin. 2. Each bin compartment can accept any number of bosons. Consider placing Ni bosons into the di compartments of the ith bin. Let the bosons be represented by Ni dots on a line. By inserting di 1 partitions, the dots are “placed” into di compartments. If the dots & partitions are all distinct, the number of all possible arrangement is However, the dots & partitions are indistinguishable among themselves. Hence

5. 4. 3. The Most Probable Configuration An isolated system in thermal equilibrium has a fixed total energy E, and fixed number of particle N , i. e. , Since each possible way to share E among N particles has the same probability to exist, the most probable configuration (N 1 , N 2 , N 3 , . . . ) is the one with the maximum Q(N 1 , N 2 , N 3 , . . . ). Since Q(N 1 , N 2 , N 3 , . . . ) involves a lot of factorials, it’s easier to work with ln. Q.

Lagrange Multipliers Problem is to maximize ln Q, subject to constraints and Using Lagrange’s multiplier method, we maximize, without constraint, i. e. , we set Note : are just the original constraints.

Distinguishable Particles Stirling’s approximation : for z >>1

Fermions di , Ni >>1 :
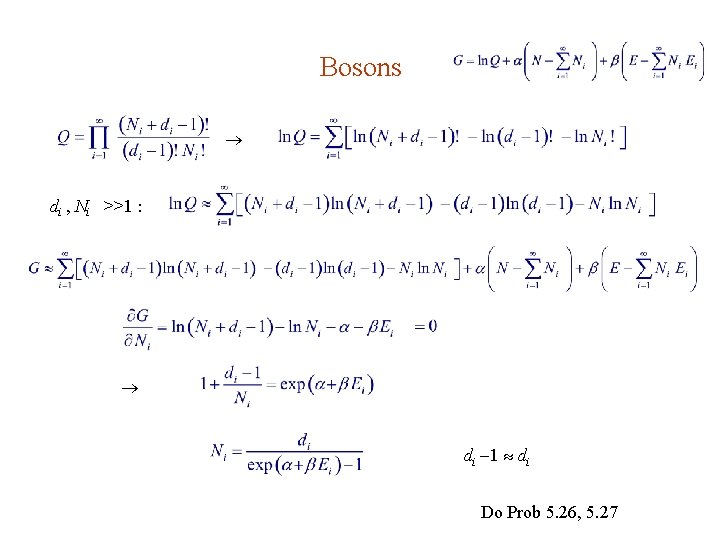
Bosons di , Ni >>1 : di 1 di Do Prob 5. 26, 5. 27

5. 4. 4. Physical Significance of and Ideal gas in 3 -D infinite square well. Taking the “bin” as the spherical shell between k and k+dk, the degeneracy dk is just the number of states in the shell :

Distinguishable Particles cf. kinetic theory result : universal

Distributions D Maxwell – Boltzmann Set F B Fermi – Dirac Bose Einstein Chemical potential n( ) Most probable number of particles in a state with energy . occupation number

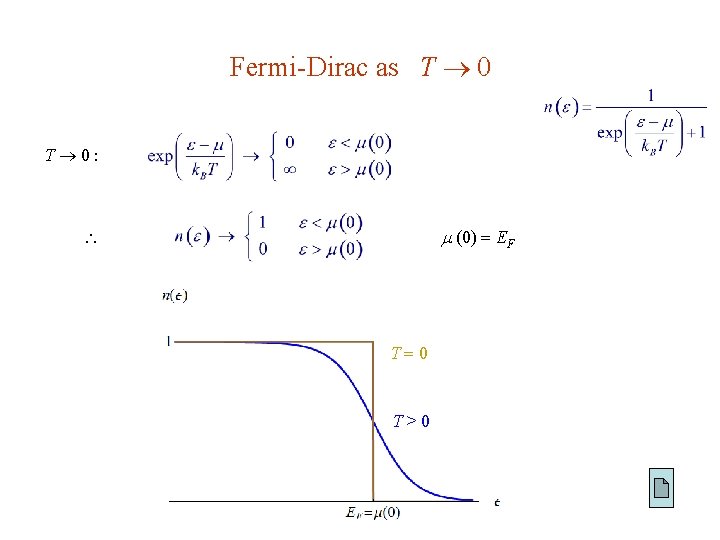
Fermi-Dirac as T 0 T 0: (0) EF T 0 T>0

Ideal Gas Distinguishable particles Indistinguishable particles : F B fixes F B Read Prob. 5. 29 Do Prob 5. 28 gives

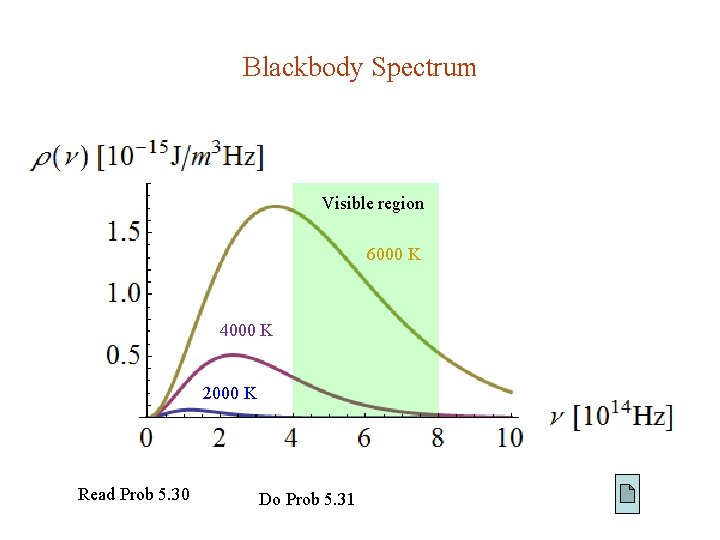
5. 4. 5. The Blackbody Spectrum Photon quantum of EM field spin 1, massless boson with v c. Only m 1 occurs. Number not conserved 0. Energy density in range d Black body spectrum

Blackbody Spectrum Visible region 6000 K 4000 K 2000 K Read Prob 5. 30 Do Prob 5. 31
 Chap chap slide
Chap chap slide Identical by descent vs identical by state
Identical by descent vs identical by state Identical particles
Identical particles Systems of particles
Systems of particles Fashion clothes meaning
Fashion clothes meaning Passion chap 6
Passion chap 6 Bank run chap 11
Bank run chap 11 Durbin chap
Durbin chap Garlic riddle
Garlic riddle Kstn chap 18
Kstn chap 18 Close family chapter 3
Close family chapter 3 The origin of species bl chapter 24
The origin of species bl chapter 24 Items purchased to satisfy needs and wants
Items purchased to satisfy needs and wants The origin of species ch 22
The origin of species ch 22 Mad dog symbolism in to kill a mockingbird
Mad dog symbolism in to kill a mockingbird Matthew 5:30
Matthew 5:30 Child development chapter 1
Child development chapter 1 Rivalry 1 chap 6
Rivalry 1 chap 6 System engineer chap 1
System engineer chap 1 Chap tree
Chap tree Kstn chap 7
Kstn chap 7 I was in that state when a chap easily turns nasty analysis
I was in that state when a chap easily turns nasty analysis The origin of species chapter 24
The origin of species chapter 24 Passion chap 9
Passion chap 9 Bài tập về nhà
Bài tập về nhà In the summer chap 22
In the summer chap 22 Selection project chap
Selection project chap Name:the origin of species ch:18
Name:the origin of species ch:18 Define the relationship chapter 12
Define the relationship chapter 12 Fitness ch 1
Fitness ch 1 Chap tree
Chap tree Chap 3 map
Chap 3 map Chap 23
Chap 23 Payback ch 12
Payback ch 12 Summerize
Summerize Youjip
Youjip In the time of the butterflies chapter 9
In the time of the butterflies chapter 9 Building customer relationship in service marketing
Building customer relationship in service marketing Payback chap 9
Payback chap 9 Swapping chapter 6
Swapping chapter 6 Sternberg love types
Sternberg love types Breath at the same air chapter 1
Breath at the same air chapter 1 What is the fundamental challenge of dashboard design
What is the fundamental challenge of dashboard design Chap 24
Chap 24 Into the light chapter 22
Into the light chapter 22 To not die chap 18
To not die chap 18 Payback chapter q
Payback chapter q Payback criterion formula
Payback criterion formula Define the relationship chapter 11
Define the relationship chapter 11 Fitness chap 1
Fitness chap 1 Pleasure principle chap 1
Pleasure principle chap 1 Why does nana forbid mariam to go to school
Why does nana forbid mariam to go to school Chap counter
Chap counter Kip chap
Kip chap Chap de direction
Chap de direction C chap
C chap Chap 22
Chap 22 The chap book
The chap book