CHAOTIC DYNAMICS IN COLLECTIVE MODELS OF NUCLEI Pavel

CHAOTIC DYNAMICS IN COLLECTIVE MODELS OF NUCLEI Pavel Stránský 1, 2 1 Institute of Particle and Nuclear Phycics Faculty of Mathematics and Physics Charles University in Prague, Czech Republic 2 Instituto de Ciencias Nucleares Universidad Nacional Autonoma de México Collaborators: Michal Macek 1, Pavel Cejnar 1 Alejandro Frank 2, Ruben Fossion 2, Emmanuel Landa 2 XXXIII Symposium on Nuclear Physics, Cocoyoc, Mexico, 2010 5 th January 2010

CHAOTIC DYNAMICS IN COLLECTIVE MODELS OF NUCLEI Introduction - Basics of Geometric Collective Model (GCM) (restricted to nonrotating motions) 1. Classical chaos in GCM - Measures of regularity - Geometrical method 2. Quantum chaos in GCM - Short-range correlations and Brody parameter Peres lattices Long-range correlations and 1/f noise Comparison of classical and quantum dynamics 3. Interacting Boson Model (IBM) - Application of the above mentioned methods

Geometrical Collective Model (restricted to nonrotating motions)

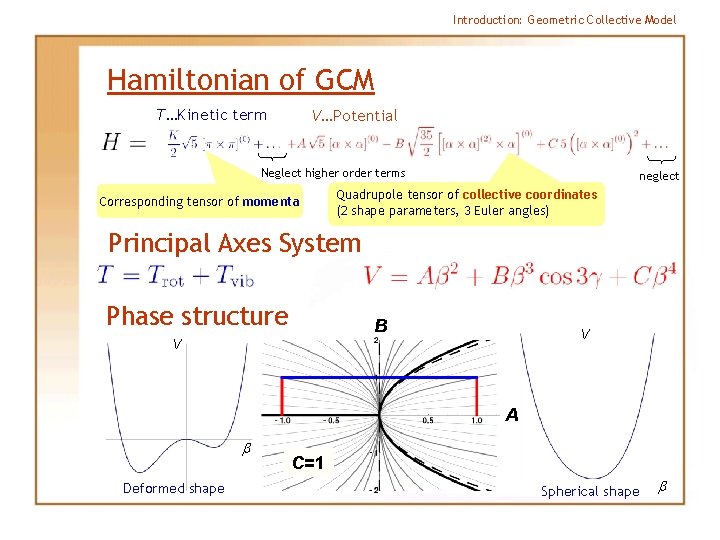
Introduction: Geometric Collective Model Hamiltonian of GCM T…Kinetic term V…Potential Neglect higher order terms Corresponding tensor of momenta Quadrupole tensor of collective coordinates (2 shape parameters, 3 Euler angles) Principal Axes System Shape variables: B … strength of nonintegrability (B = 0 – integrable quartic oscillator) neglect

Introduction: Geometric Collective Model Hamiltonian of GCM T…Kinetic term V…Potential Neglect higher order terms Corresponding tensor of momenta neglect Quadrupole tensor of collective coordinates (2 shape parameters, 3 Euler angles) Principal Axes System Phase structure B V V A b Deformed shape C=1 Spherical shape b

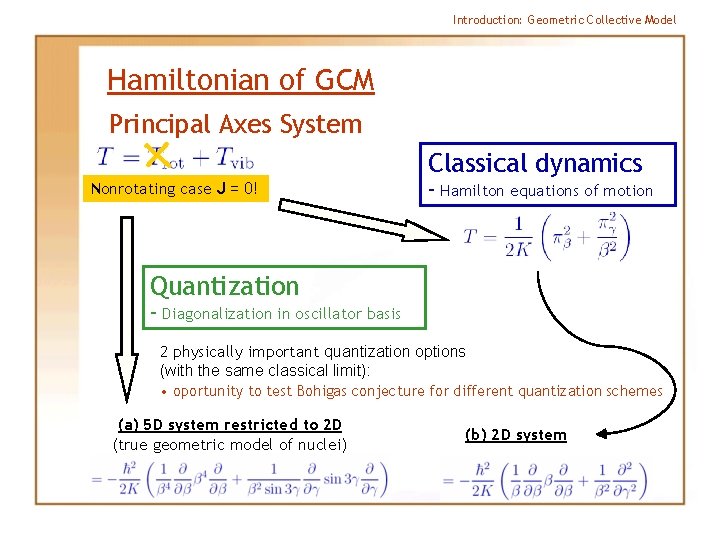
Introduction: Geometric Collective Model Hamiltonian of GCM Principal Axes System Classical dynamics Nonrotating case J = 0! – Hamilton equations of motion Quantization – Diagonalization in oscillator basis 2 physically important quantization options (with the same classical limit): • oportunity to test Bohigas conjecture for different quantization schemes (a) 5 D system restricted to 2 D (true geometric model of nuclei) (b) 2 D system

1. Classical chaos in GCM

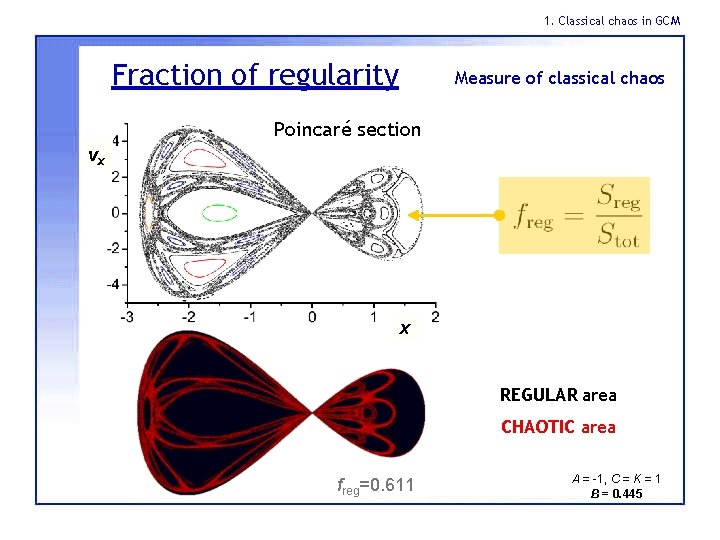
1. Classical chaos in GCM Fraction of regularity Measure of classical chaos Poincaré section vx x REGULAR area CHAOTIC area freg=0. 611 A = -1, C = K = 1 B = 0. 445

1. Classical chaos in GCM Different definitons & comparison Surface of chosen Poincaré section number of regular total trajectories (with random initial conditions) Statistical measure E=0 control parameter

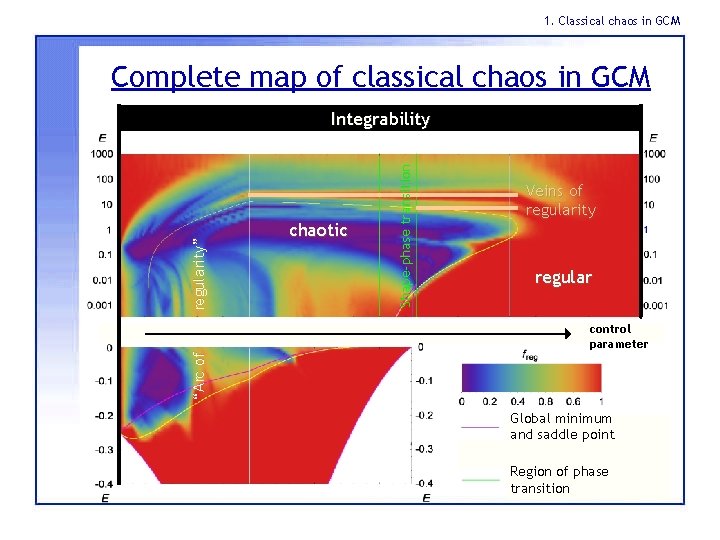
1. Classical chaos in GCM Complete map of classical chaos in GCM chaotic Shape-phase transition regularity” Integrability Veins of regularity regular “Arc of control parameter Global minimum and saddle point Region of phase transition

1. Classical chaos in GCM Geometrical method Hamiltonian in flat Eucleidian space with potential: Conformal metric Hamiltonian of free particle in curved space: Application of methods of Riemannian geometry Negative eigenvalues of the matrix inside kinematically accesible area induce nonstability. L. Horwitz et al. , Phys. Rev. Lett. 98 (2007), 234301

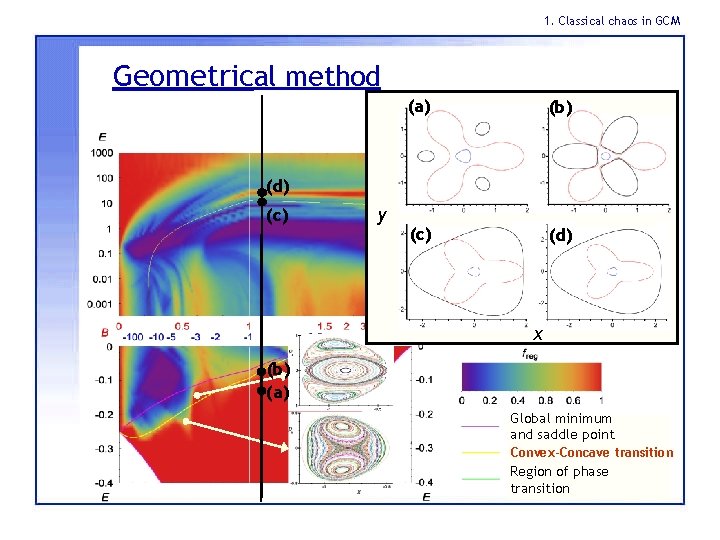
1. Classical chaos in GCM Geometrical method (a) (b) (c) (d) (c) y x (b) (a) Global minimum and saddle point Convex-Concave transition Region of phase transition

2. Quantum chaos in GCM

2. Quantum chaos in GCM Spectral statistics Nearestneighbor spacing distribution P(s) Poisson GOE s REGULAR system CHAOTIC system Brody distribution parameter w - Artificial interpolation between Poisson and GOE distribution - Measure of chaoticity of quantum systems - Tool to test classical-quantum correspondence Bohigas conjecture (O. Bohigas, M. J. Giannoni, C. Schmit, Phys. Rev. Lett. 52 (1984), 1)

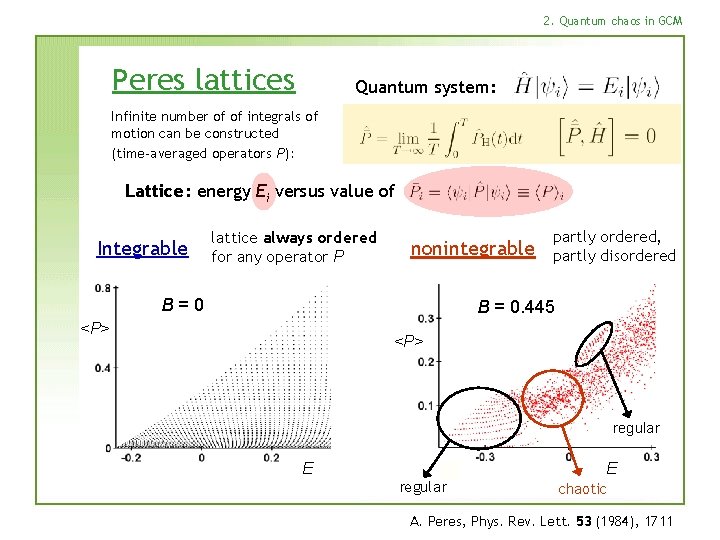
2. Quantum chaos in GCM Peres lattices Quantum system: Infinite number of of integrals of motion can be constructed (time-averaged operators P): Lattice: energy Ei versus value of Integrable lattice always ordered for any operator P nonintegrable B=0 partly ordered, partly disordered B = 0. 445 <P> regular E E regular chaotic A. Peres, Phys. Rev. Lett. 53 (1984), 1711

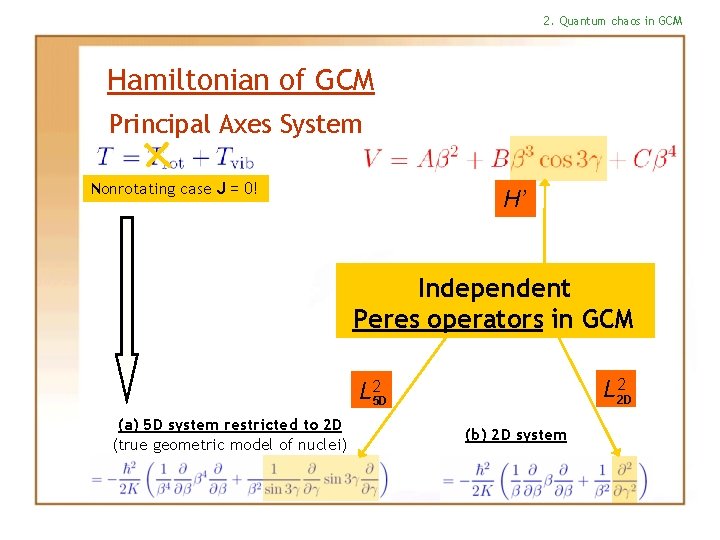
2. Quantum chaos in GCM Hamiltonian of GCM Principal Axes System Nonrotating case J = 0! H’ Independent Peres operators in GCM L 22 D L 25 D (a) 5 D system restricted to 2 D (true geometric model of nuclei) (b) 2 D system

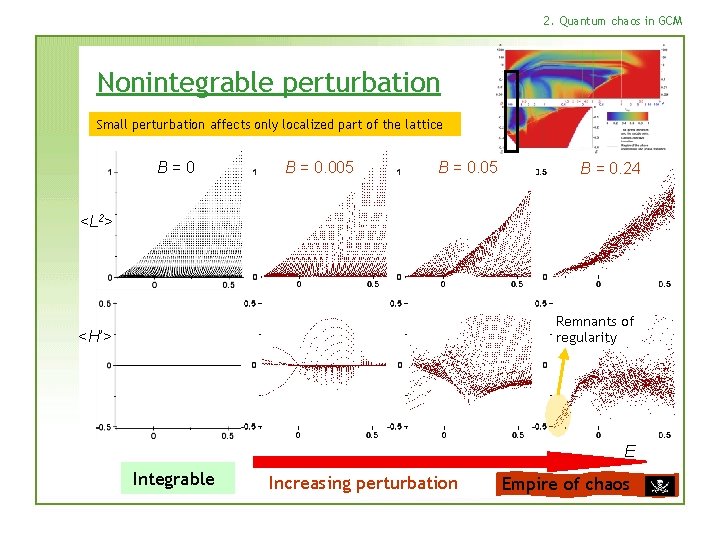
2. Quantum chaos in GCM Nonintegrable perturbation Small perturbation affects only localized part of the lattice B=0 B = 0. 005 B = 0. 24 <L 2> Remnants of regularity <H’> E Integrable Increasing perturbation Empire of chaos

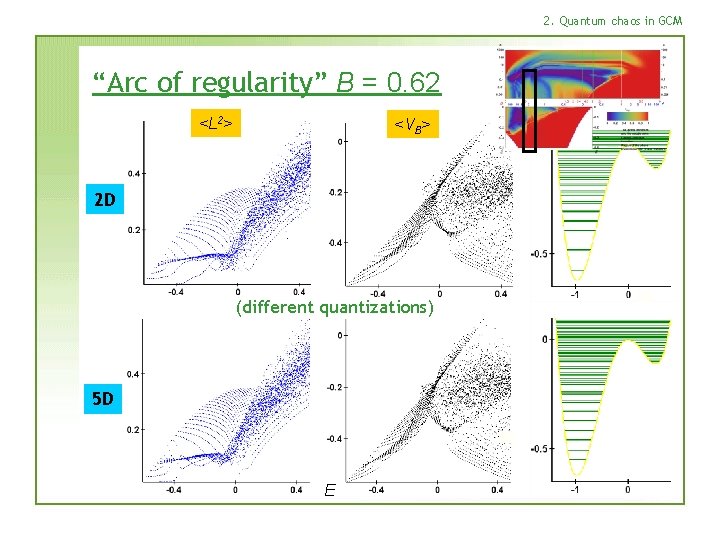
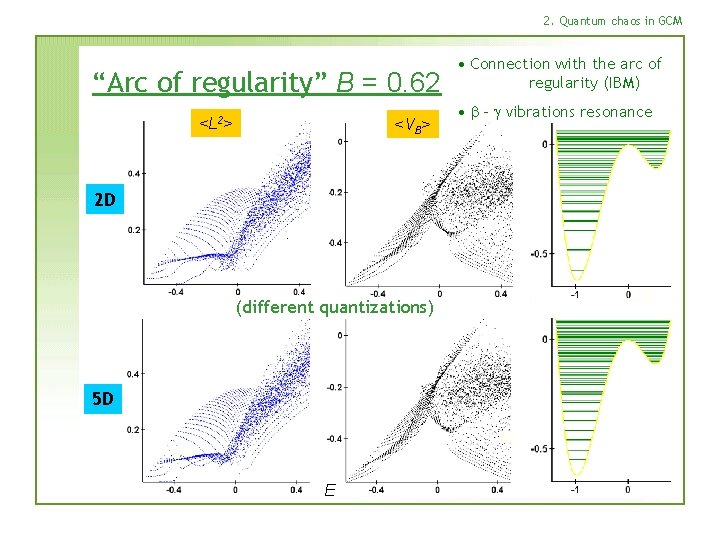
2. Quantum chaos in GCM “Arc of regularity” B = 0. 62 <L 2> <VB> 2 D (different quantizations) 5 D E

2. Quantum chaos in GCM “Arc of regularity” B = 0. 62 <L 2> <VB> 2 D (different quantizations) 5 D E • Connection with the arc of regularity (IBM) • b – g vibrations resonance

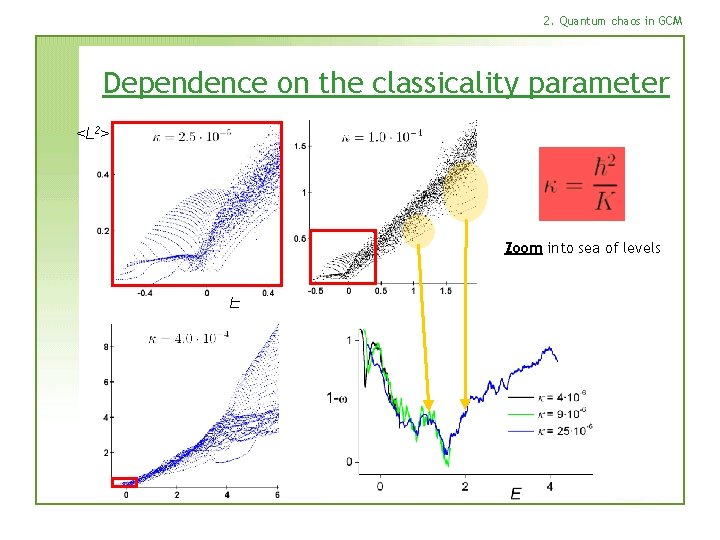
2. Quantum chaos in GCM Dependence on the classicality parameter <L 2> Zoom into sea of levels E

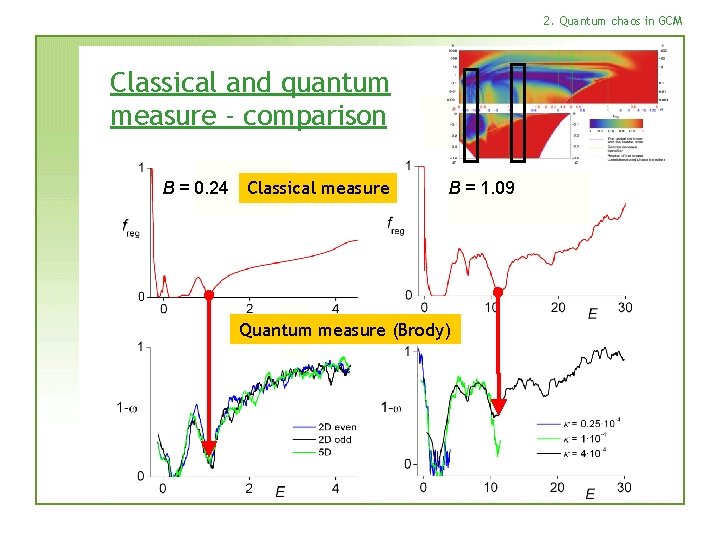
2. Quantum chaos in GCM Classical and quantum measure - comparison B = 0. 24 Classical measure B = 1. 09 Quantum measure (Brody)

2. Quantum chaos in GCM 1/f noise - Fourier transformation of the time series Power spectrum a=1 CHAOTIC system a=2 REGULAR system - Direct comparison of - In GCM we cannot average over ensembles!!! A. Relaño et al. , Phys. Rev. Lett. 89, 244102 (2002)

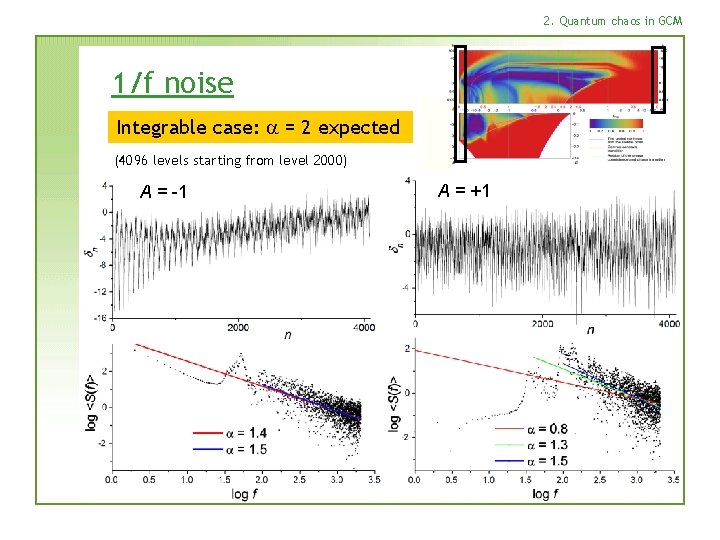
2. Quantum chaos in GCM 1/f noise Integrable case: a = 2 expected (4096 levels starting from level 2000) A = -1 A = +1

2. Quantum chaos in GCM 1/f noise Comparison of measures B = 0. 24 B = 0. 62

3. Chaos in IBM 3. Interacting Boson Model

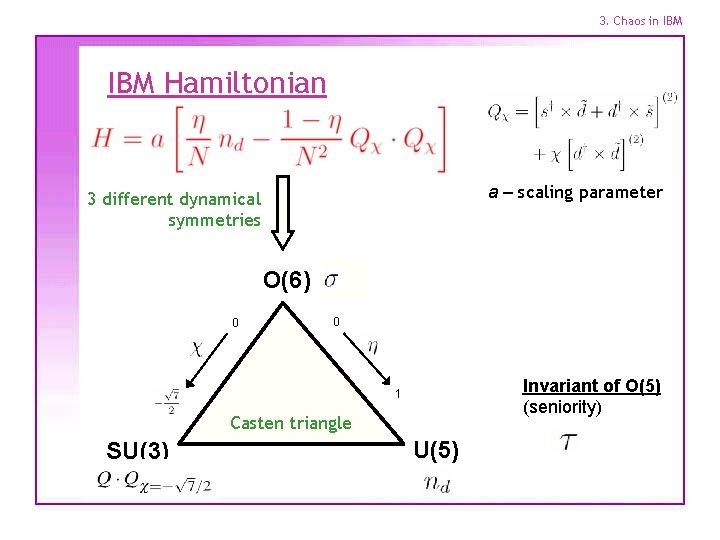
3. Chaos in IBM Hamiltonian a – scaling parameter 3 different dynamical symmetries O(6) 0 0 Invariant of O(5) (seniority) 1 Casten triangle SU(3) U(5)

3. Chaos in IBM Hamiltonian a – scaling parameter 3 different dynamical symmetries 3 different Peres operators O(6) 0 0 Invariant of O(5) (seniority) 1 Casten triangle SU(3) U(5)

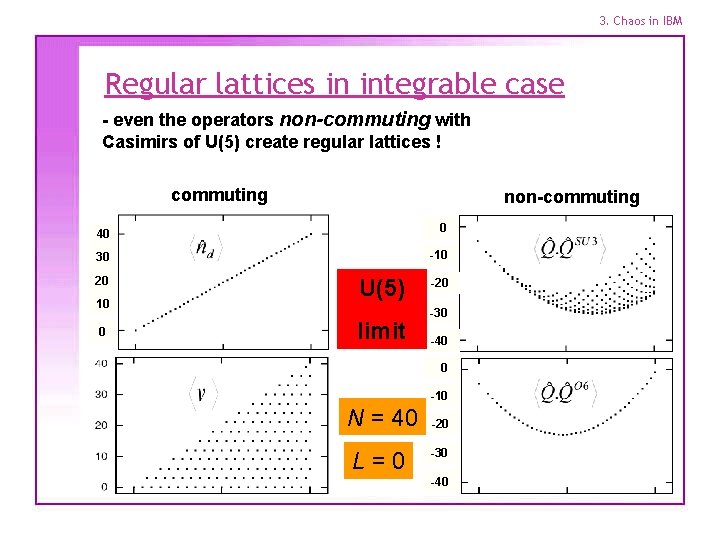
3. Chaos in IBM Regular lattices in integrable case - even the operators non-commuting with Casimirs of U(5) create regular lattices ! commuting non-commuting 0 40 -10 30 20 10 0 U(5) limit -20 -30 -40 0 -10 N = 40 L=0 -20 -30 -40

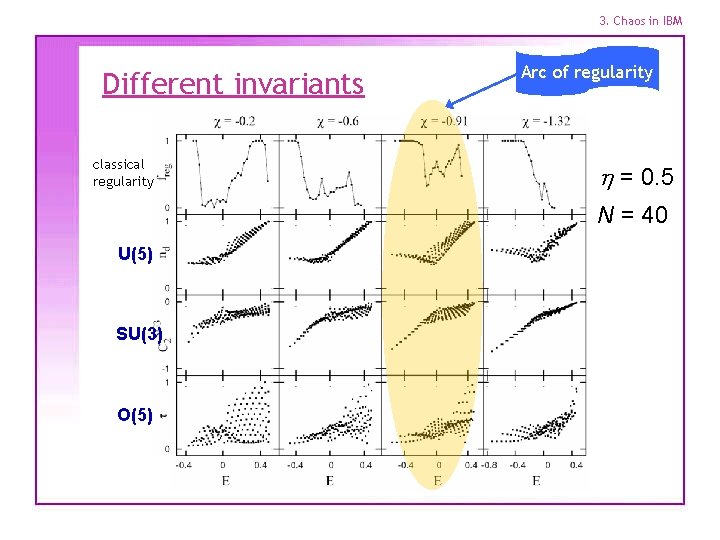
3. Chaos in IBM Different invariants classical regularity Arc of regularity h = 0. 5 N = 40 U(5) SU(3) O(5)

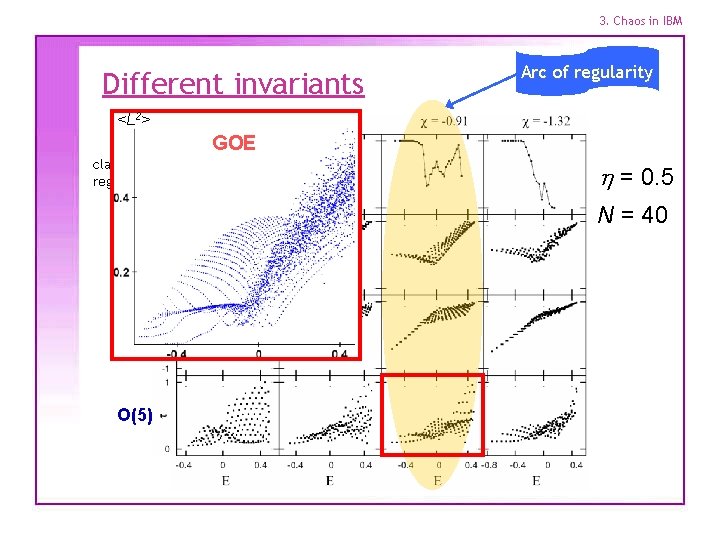
3. Chaos in IBM Different invariants Arc of regularity <L 2> GOE classical regularity h = 0. 5 N = 40 U(5) SU(3) O(5)

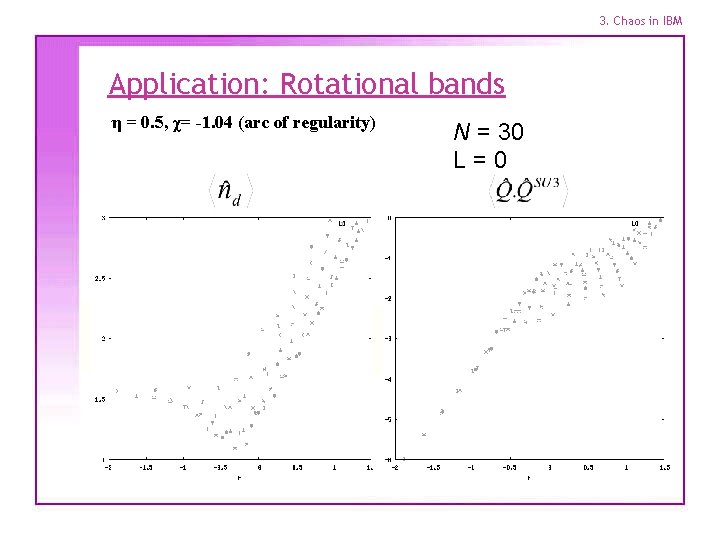
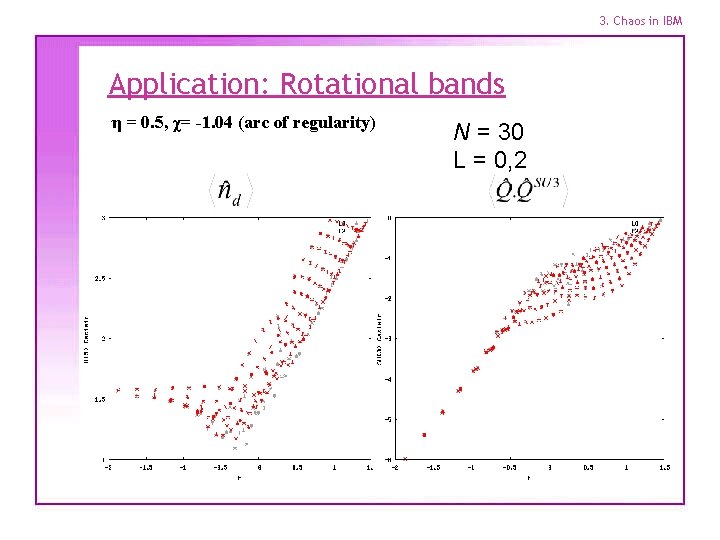
3. Chaos in IBM Application: Rotational bands η = 0. 5, χ= -1. 04 (arc of regularity) N = 30 L=0

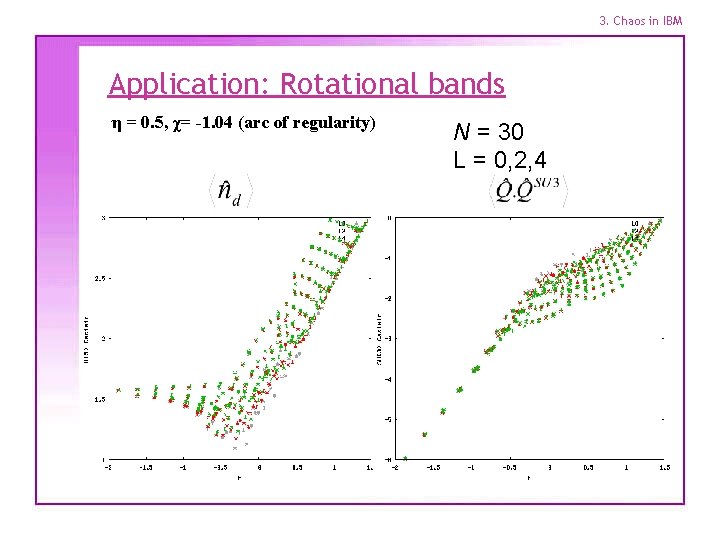
3. Chaos in IBM Application: Rotational bands η = 0. 5, χ= -1. 04 (arc of regularity) N = 30 L = 0, 2

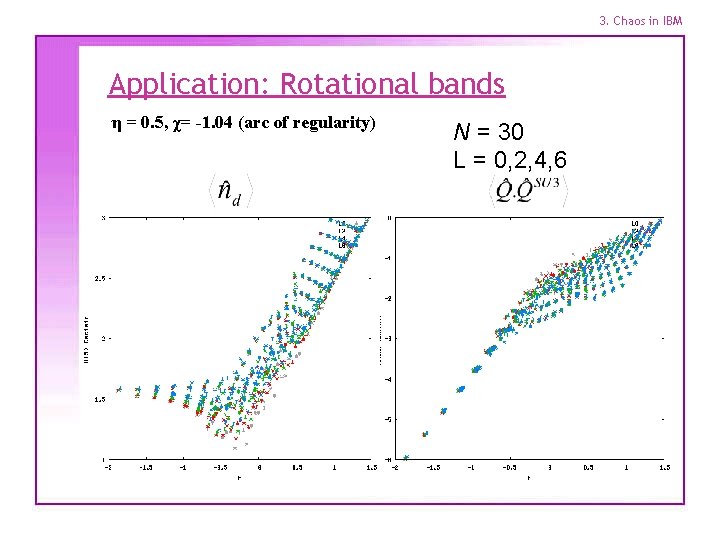
3. Chaos in IBM Application: Rotational bands η = 0. 5, χ= -1. 04 (arc of regularity) N = 30 L = 0, 2, 4

3. Chaos in IBM Application: Rotational bands η = 0. 5, χ= -1. 04 (arc of regularity) N = 30 L = 0, 2, 4, 6

This is the last slide Summary Thank you for your attention 1. Collective models of nuclei • • Complex behavior encoded in simple dynamical equation Possibility of studying manifestations of both classical and quantum chaos and their relation 2. Peres lattices • • Allow visualising quantum chaos Capable of distinguishing between chaotic and egular parts of the spectra Freedom in choosing Peres operator • 3. Methods of Riemannian geometry • Determine location of the onset of chaoticity in classical systems 4. 1/f Noise • Preliminary results, deeper investigation should be done http: //www-ucjf. troja. mff. cuni. cz/~geometric ~stransky