Channel Models Data Communication lecture 10 1 Introduction

Channel Models Data Communication lecture 10 1

Introduction • Propagation models are fundamental tools for designing any broadband wireless communication system. • A propagation model basically predicts what will happen to the transmitted signal while in transit to the receiver • Traditionally, ‘propagation models’ is the term applied to those algorithms and methods used to predict the median signal level at the receiver. • Such models include signal level information, signal time dispersion information and, in the case of mobile systems, models of Doppler shift distortions arising from the motion of the mobile. Data Communication lecture 10 2

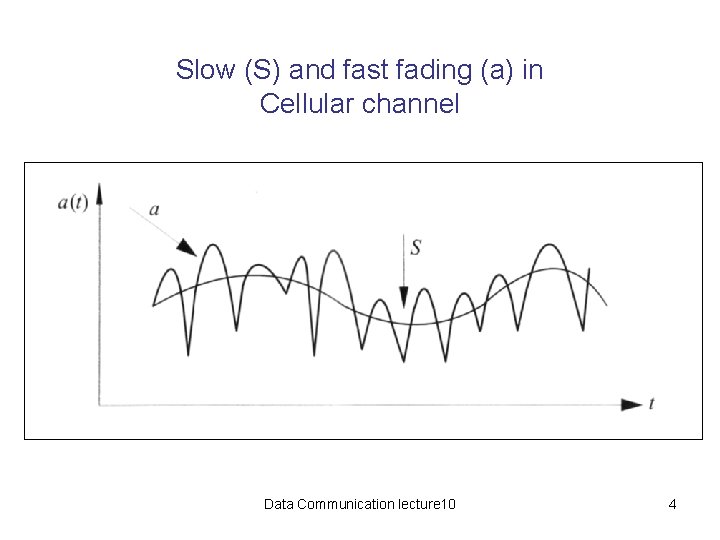
Fading • Fluctuation in the strength of signal, because of variations in the transmission medium. • Fading is a broad term applied to a wide range of variation in the signal amplitude, phase, and frequency characteristic. • For example, the term ‘shadow fading‘ is used to describe the decrease in signal strength that is observed when a mobile terminal is behaind a building. Data Communication lecture 10 3

Slow (S) and fast fading (a) in Cellular channel Data Communication lecture 10 4

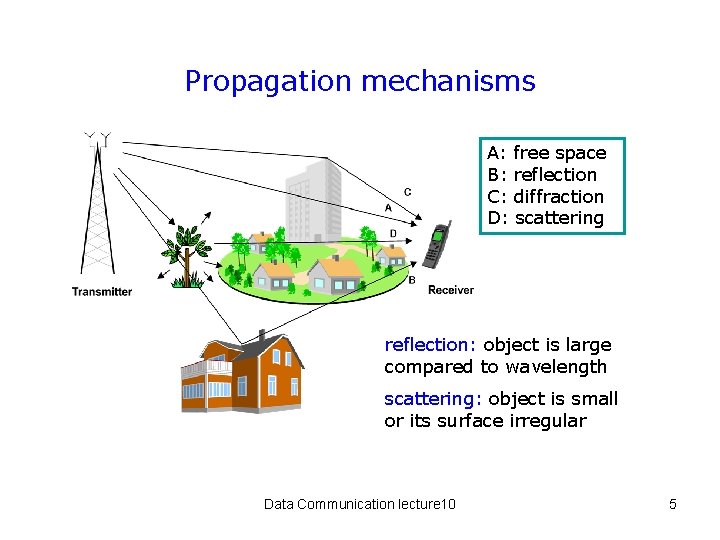
Propagation mechanisms A: freespace A: B: reflection B: C: diffraction C: D: scattering D: reflection: object is large compared to wavelength scattering: object is small or its surface irregular Data Communication lecture 10 5

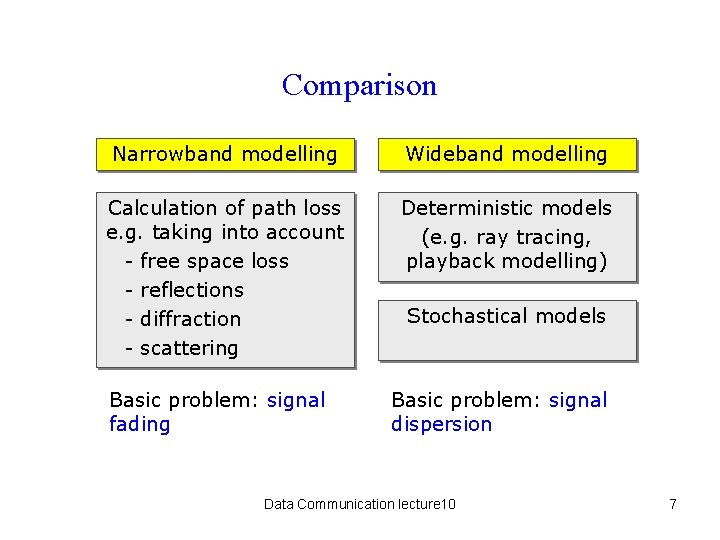
Radio channel modelling Narrowband Models Wideband Models • Because the signal • The bandwidth of the bandwidth is narrow, the signal, sent through the fading mechanism will channel is such that time affect all frequencies in dispersion information is the signal passband required. equally. • Time dispersion causes • So, a narrowband the signal fading to vary as channel is often referred a function of frequency, so to as a flat-fading channel. wideband channels are often called frequencyselective fading channels. Data Communication lecture 10 6

Comparison Narrowband modelling Wideband modelling Calculation of path loss e. g. taking into account - free space loss - reflections - diffraction - scattering Deterministic models (e. g. ray tracing, playback modelling) Basic problem: signal fading Stochastical models Basic problem: signal dispersion Data Communication lecture 10 7

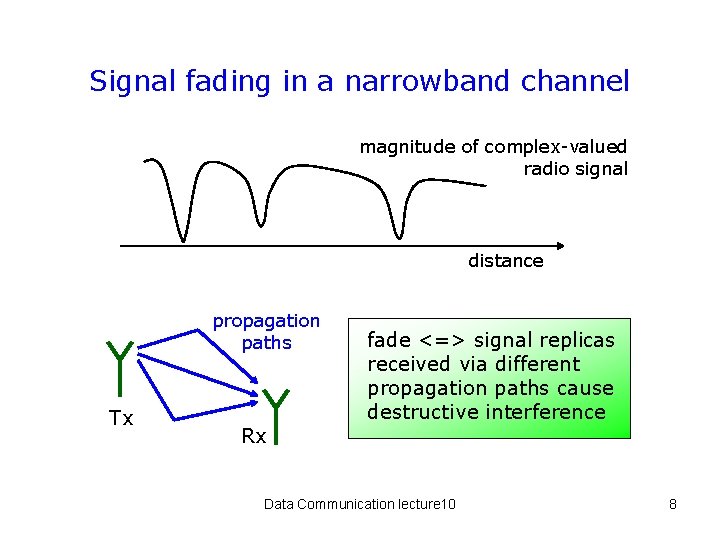
Signal fading in a narrowband channel magnitude of complex-valued radio signal distance propagation paths Tx Rx fade <=> signal replicas received via different propagation paths cause destructive interference Data Communication lecture 10 8

Low-pass equivalent (LPE) signal RF carrier frequency Real-valued RF signal In-phase signal component Complex-valued LPE signal Quadrature component Data Communication lecture 10 9

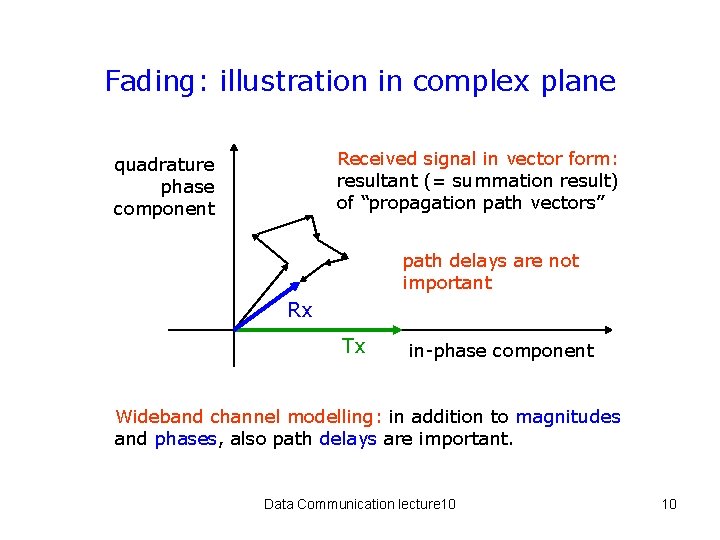
Fading: illustration in complex plane Received signal in vector form: resultant (= summation result) of “propagation path vectors” quadrature phase component path delays are not important Rx Tx in-phase component Wideband channel modelling: in addition to magnitudes and phases, also path delays are important. Data Communication lecture 10 10

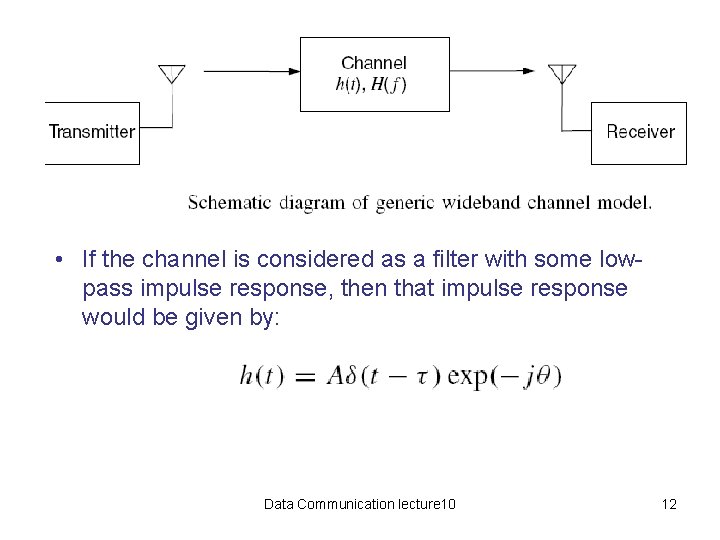
Generic Wideband Channel Model • Wideband generally indicates those channels in which time dispersion and frequency-selective fading have a significant impact on the signal being transmitted. • For signals whose occupied bandwidth is narrow compared to the correlation bandwidth of the channel, the generic wideband model simplifies to a narrowband model in which many elements of the wideband model may be discarded. Data Communication lecture 10 11

• If the channel is considered as a filter with some lowpass impulse response, then that impulse response would be given by: Data Communication lecture 10 12

• A sinewave signal at frequency ω leaving the transmitting antenna would arrive at the receiver reduced in amplitude by factor A, shifted in phase by θ, and delayed by τ seconds. • Such a model of the transmission channel is applicable for free-space propagation conditions in which signal energy arrives at the receiver directly (via one path) from the transmitter. Data Communication lecture 10 13

• If the channel consisted of two transmission paths for the transmitted energy to arrive at the receiver (for example, with the addition of a single ground reflection), the channel impulse response would be the sum of the effect of the two paths: • This is the impulse response of the so-called ‘two-ray’ channel model. Data Communication lecture 10 14

• For N possible transmission paths, h(t) becomes: • This is the channel impulse response to a particular point p 2(x 2, y 2, z 2) from a transmitter located at point p 1(x 1, y 1, z 1). LOS path Data Communication lecture 10 15

Example: multipath signal The received multipath signal is the sum of N attenuated, phase shifted and delayed replicas of the transmitted signal s(t) T Tm : Normalized delay spread D = Tm / T Data Communication lecture 10 16

Important Note: The normalized delay spread is an important quantity. When D << 1, the channel is - narrowband - frequency-nonselective - flat and there is no intersymbol interference (ISI). When D approaches or exceeds unity, the channel is - wideband - frequency selective - time dispersive Data Communication lecture 10 17

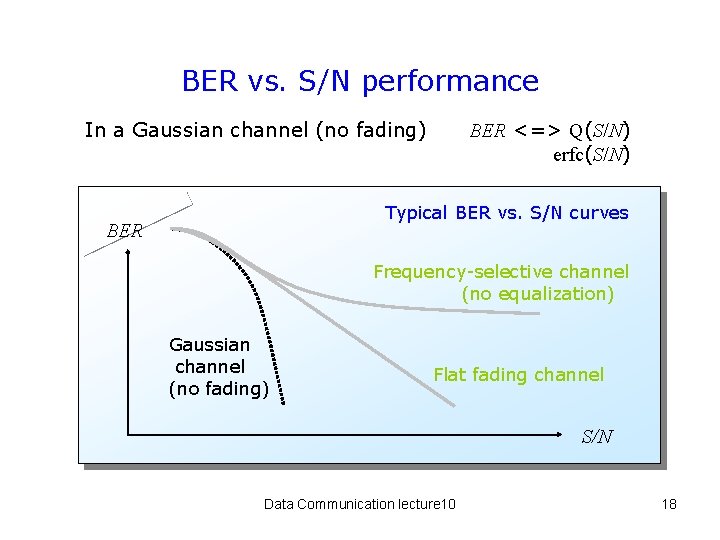
BER vs. S/N performance In a Gaussian channel (no fading) BER <=> Q(S/N) erfc(S/N) Typical BER vs. S/N curves BER Frequency-selective channel (no equalization) Gaussian channel (no fading) Flat fading channel S/N Data Communication lecture 10 18

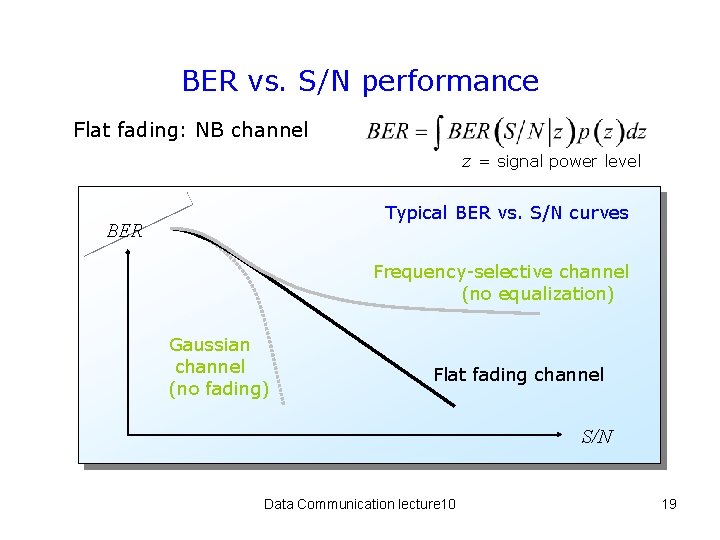
BER vs. S/N performance Flat fading: NB channel z = signal power level Typical BER vs. S/N curves BER Frequency-selective channel (no equalization) Gaussian channel (no fading) Flat fading channel S/N Data Communication lecture 10 19

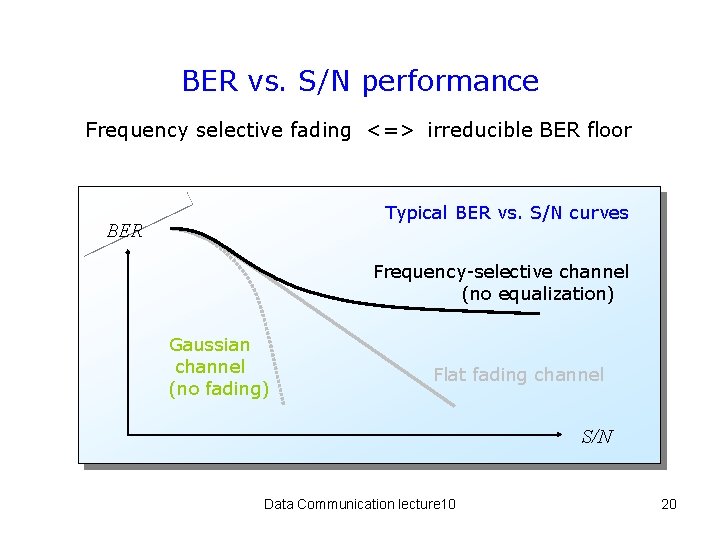
BER vs. S/N performance Frequency selective fading <=> irreducible BER floor Typical BER vs. S/N curves BER Frequency-selective channel (no equalization) Gaussian channel (no fading) Flat fading channel S/N Data Communication lecture 10 20

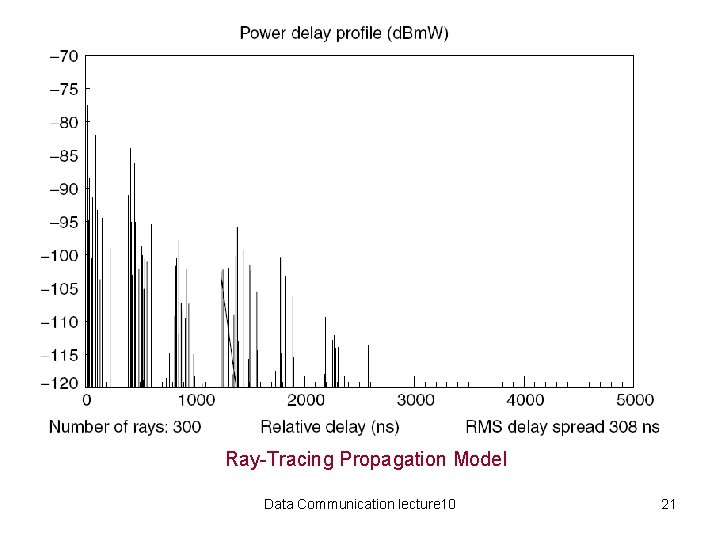
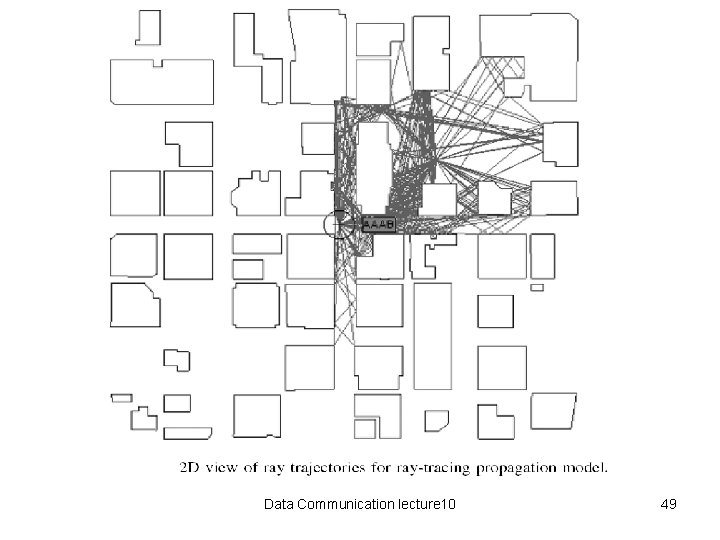
Ray-Tracing Propagation Model Data Communication lecture 10 21

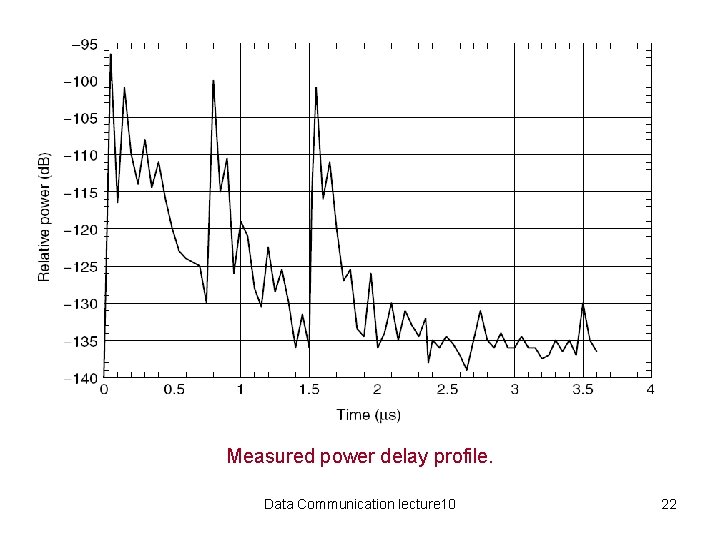
Measured power delay profile. Data Communication lecture 10 22

RMS Delay spread • A common measure of the amount of time dispersion in a channel is the RMS delay spread. • The RMS delay spread can be found from the power delay profile: Data Communication lecture 10 23

Generic Model, Continue • The more general impulse response can thus be written as: • Here, the number, amplitude, phase, and time delay of the components of the summation are a function of the location of the transmit and receive antenna points in the propagation space. • This equation is for a single static point in space. Data Communication lecture 10 24

• For mobile communication, the receiver is often moving. • That motion can affect the phase relationship of the components of this equation, in a way that may be important to data symbols being transmitted. • This motion will result in a frequency or Doppler shift of the received signal, which will be a function of speed and direction of motion, and the angle of arrival (AOA) of the signal energy. Data Communication lecture 10 25

• Modification to include the Doppler shift: • Here, Δθn is a phase displacement due to the motion. Data Communication lecture 10 26

Doppler Shift • For a mobile receiver: • φn is the arrival angle of the nth component, v is the speed of motion, φv is the direction of motion, and λ is the wavelength. Data Communication lecture 10 27

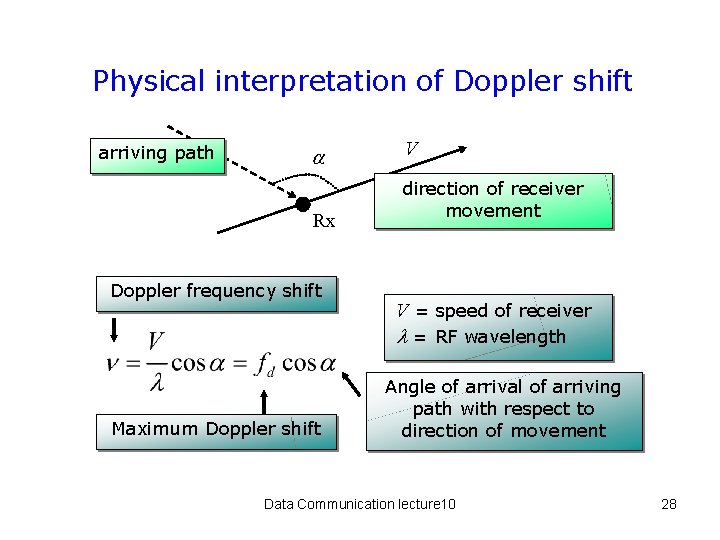
Physical interpretation of Doppler shift arriving path Rx Doppler frequency shift V direction of receiver movement V = speed of receiver l = RF wavelength Maximum Doppler shift Angle of arrival of arriving path with respect to direction of movement Data Communication lecture 10 28

• In general, the amplitudes An and phase shifts θn, will be functions of the carrier frequency ω, thus: Data Communication lecture 10 29

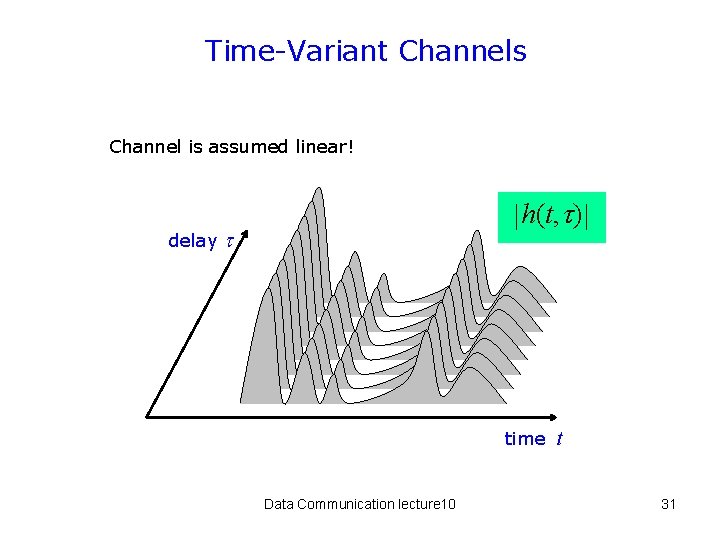
Time-Variant Channels • To deal with a time-variant channel, we define the input delay-spread function h(t, τ ). • This is the low-pass response of the channel at some time t to a unit impulse function input at some previous time τ seconds earlier. • Note that this delay τ is different from the discrete τ1, τ2. . . τn arrival delay times, that define when the signal waves reach the receiver. Data Communication lecture 10 30

Time-Variant Channels Channel is assumed linear! delay h(t, ) time Data Communication lecture 10 t 31

Time-Variant Channels • The output of the channel y(t) can then be found by the convolution of the input signal um(t) with h(t, τ ) integrated over the delay variable τ: Data Communication lecture 10 32

Data Communication lecture 10 33

Data Communication lecture 10 34

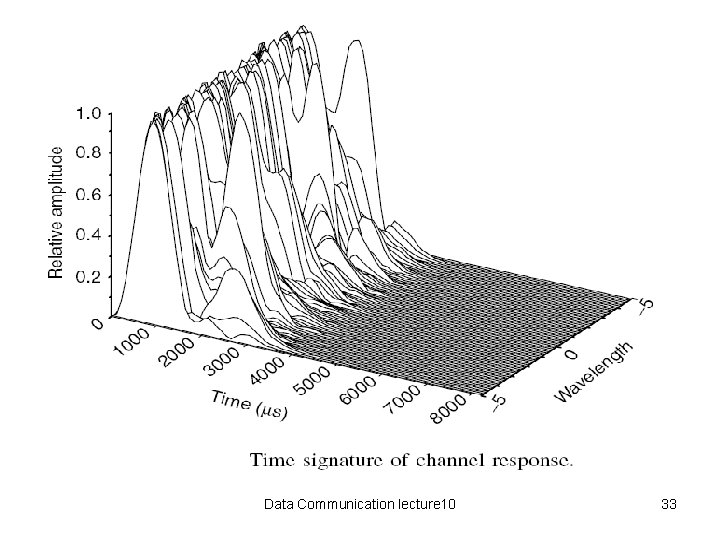
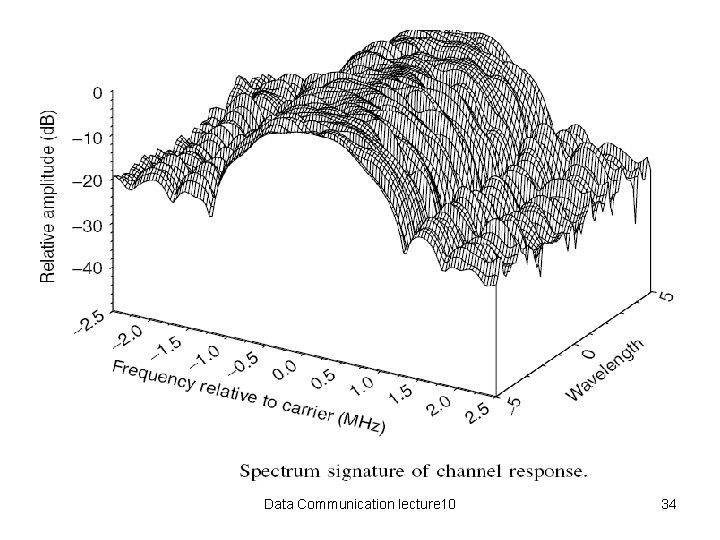
Some Notes • Using an impulse response from a ray-tracing propagation model, and convolving it with a raised cosine symbol pulse, the result is a time signature of the channel. • The variations in signatures are due to the relative phase changes, and not changing amplitudes. • By taking the Fourier Transform of the time signatures, it is possible to created spectrum signatures. • The nonuniform frequency response, represents the frequency-selective nature of the channel. Data Communication lecture 10 35

Path Loss Modeling • Maxwell’s equations – Complex and impractical • Physical Models – Free space path loss model • Too simple – Ray tracing models • Requires site-specific information • Empirical Models – Don’t always generalize to other environments Data Communication lecture 10 36

Empirical Models Commonly used in cellular system simulations • Are based on observations or measurements. • measurements are typically done in the field to measure path loss, delay spread, or other channel characteristics. • Site and field dependent Data Communication lecture 10 37

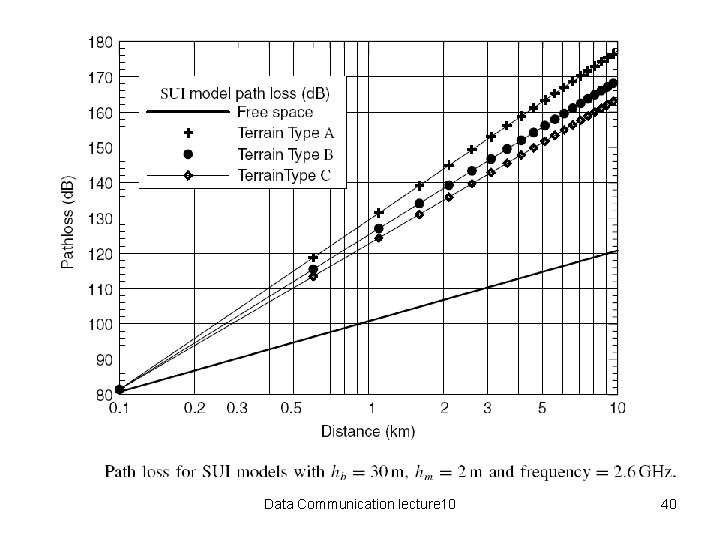
Empirical Models IEEE 802. 16 (SUI) model where d is the distance in meters, d 0 = 100 meters, hb is the base station height above ground (10 m < hb < 80 m) Data Communication lecture 10 38

Data Communication lecture 10 39

Data Communication lecture 10 40

Some Other Empirical Models • Okumura model – Empirically based (site/freq specific) • Hata model – Analytical approximation to Okumura model • Cost 136 Model: – Extends Hata model to higher frequency (2 GHz) • Walfish/Bertoni: – Cost 136 extension to include diffraction from rooftops Data Communication lecture 10 41

Physical Models Data Communication lecture 10 42

Free Space (LOS) Model d=vt • Path loss for unobstructed LOS path • Power falls off : – Proportional to d 2 – Proportional to l 2 (inversely proportional to f 2) Data Communication lecture 10 43

Two Path Model • Path loss for one LOS path and 1 ground (or reflected) bounce • Ground bounce approximately cancels LOS path above critical distance • Power falls off – Proportional to d 2 (small d) – Proportional to d 4 (d>dc) Data Communication lecture 10 44

Simplified Path Loss Model • Used when path loss dominated by reflections. • Most important parameter is the path loss exponent g, determined empirically. Data Communication lecture 10 45

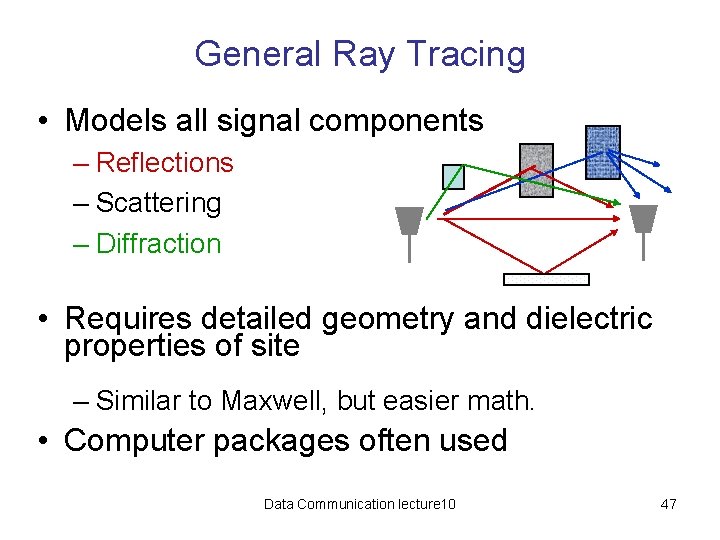
Ray Tracing Approximation • Represent wavefronts as simple particles • Geometry determines received signal from each signal component • Typically includes reflected rays, can also include scattered and defracted rays. • Requires site parameters – Geometry – Dielectric properties Data Communication lecture 10 46

General Ray Tracing • Models all signal components – Reflections – Scattering – Diffraction • Requires detailed geometry and dielectric properties of site – Similar to Maxwell, but easier math. • Computer packages often used Data Communication lecture 10 47

Data Communication lecture 10 48

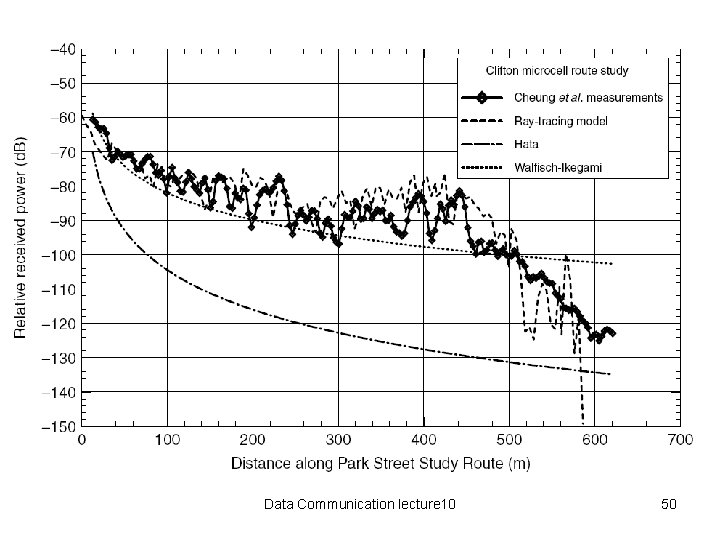
Data Communication lecture 10 49

Data Communication lecture 10 50

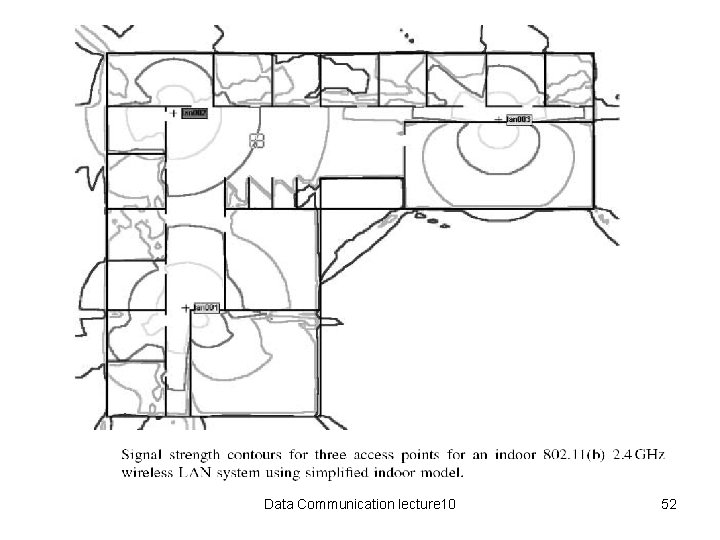
Simplified indoor model SIM • An effort to provide a fast and simple model that predicts indoor signal levels. • Worksin the area of 2. 4 GHz Wi-Fi or 5. 7 GHz U-NII band systems, intended to work over short ranges, especially indoors through walls and floors. • SIM makes use of four basic propagation primitives: line -of-sight rays, wall transmission loss, corner diffraction, and attenuation due to partial Fresnel zone obstruction Data Communication lecture 10 51

Data Communication lecture 10 52