Channel Coding in IEEE 802 16 e Student

Channel Coding in IEEE 802. 16 e Student: Po-Sheng Wu Advisor: David W. Lin 1

Reference n n IEEE Std 802. 16 a-2003, April 2003 IEEE Std 802. 16 -2004, October 2004 IEEE Std 802. 16 e™-2005 and IEEE Std 802. 16™-2004/Cor 1 -2005 IEEE Std 802. 16 e/D 9, June 2005 2

Outline n n n Overview RS code Convolution code LDPC code Future Work 3

Overview 4

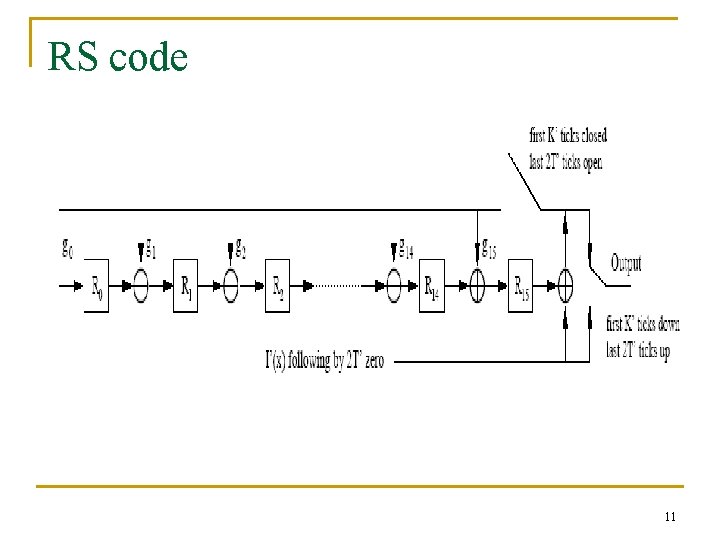
RS code n The RS code in 802. 16 a is derived from a systematic RS (N=255, K=239, T=8) code on GF(2^8) 5

RS code 6

RS code n n This code then is shortened and punctured to enable variable block size and variable errorcorrection capability. Shorten：(n, k) → (n-l, k-l) Punctured： (n, k) → (n-l, k) In general, the generator polynomial in IEEE 802. 16 a h=0 7

RS code n n n They are shortened to K’ data bytes and punctured to permit T’ bytes to be corrected. When a block is shortened to K’, the first 239 K’ bytes of the encoder input shall be zero When a codeword is punctured to permit T’ bytes to be corrected, only the first 2 T’ of the total 16 parity bytes shall be employed. 8

RS code n n When shortened and punctured to (48, 36, 6) the first 203(239 -36) information bytes are assigned 0. And only the first 12(2*6) bytes of R(X) will be employed in the codeword. 9

Shortened and Punctured 10

RS code 11

RS code n n Decoding : The Euclid’s (Berlekamp) algorithm is a common decoding algorithm for RS code. Four step: -compute the syndrome value -compute the error location polynomial -compute the error location -compute the error value 12

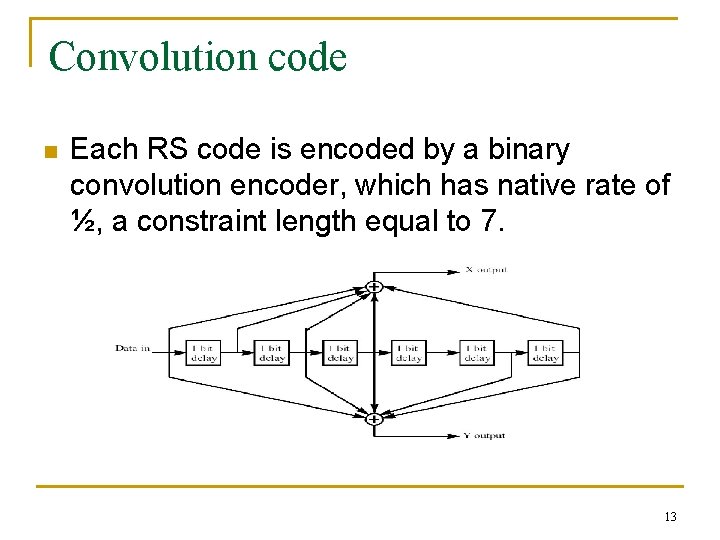
Convolution code n Each RS code is encoded by a binary convolution encoder, which has native rate of ½, a constraint length equal to 7. 13

Convolution code n “ 1” means a transmitted bit and “ 0” denotes a removed bit, note that the has been changed from that of the native convolution code with rate ½. 14

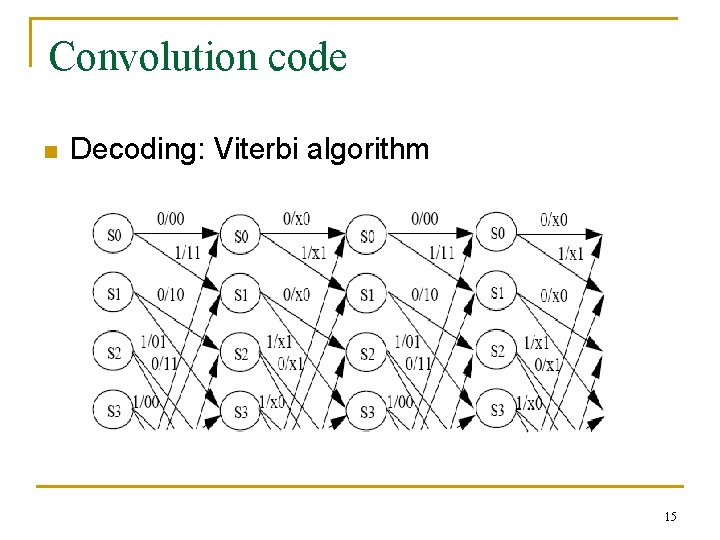
Convolution code n Decoding: Viterbi algorithm 15

Convolution code n n The convolution code in IEEE 802. 16 a need to be terminated in a block, and thus become a block code. Three method to achieve this termination q q q Direct truncation Zero tail Tail biting 16

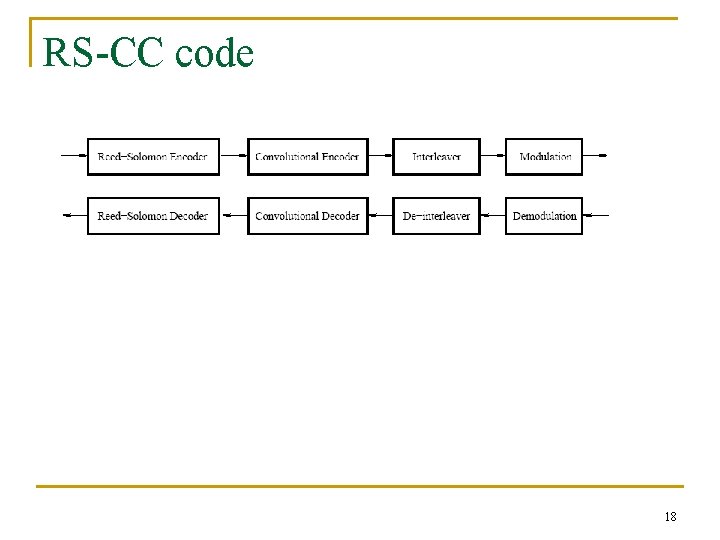
RS-CC code n n Outer code: RS code Inner code: convolution code Input data streams are divided into RS blocks, then each RS block is encode by a tail-biting convolution code. Between the convolution coder and modulator is a bit interleaver. 17

RS-CC code 18

LDPC code n n n low density parity checks matrix LDPC codes also linear codes. The codeword can be expressed as the null space of H, Hx=0 Low density enables efficient decoding q q Better decoding performance to Turbo code Close to the Shannon limit at long block length 19

LDPC code n n is the length of the code, m is the number of parity check bit 20

LDPC code n Base model 21

LDPC code n if p(f, i, j) = -1 q replace by z*z zero matrix else q p(f, i, j) is the circular shift size 22

LDPC code n Encoding [u p 1 p 2] 23

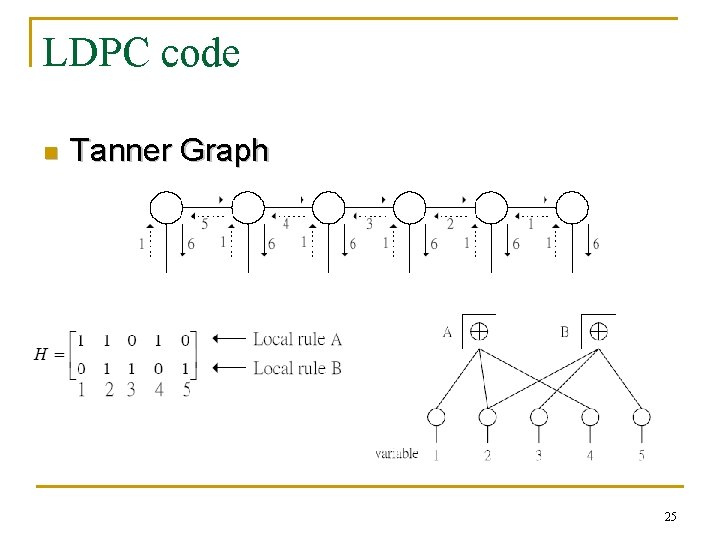
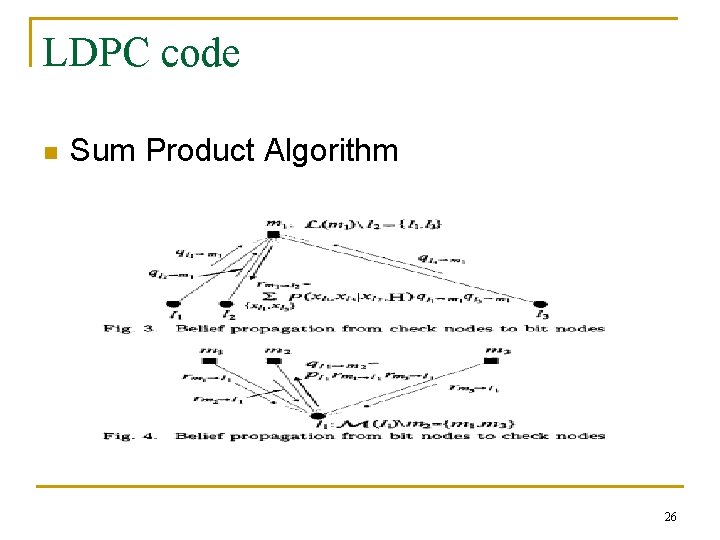
LDPC code n Decoding q q Tanner Graph Sum Product Algorithm 24

LDPC code n Tanner Graph 25

LDPC code n Sum Product Algorithm 26

LDPC code 27

LDPC code 28

Future Work n n Realize these algorithm in computer Find some decoding algorithm to speed up 29

§ Thanks for your attention 30