Channel coding architectures for OCDMA Herwin Chan July

Channel coding architectures for OCDMA Herwin Chan July 29, 2005

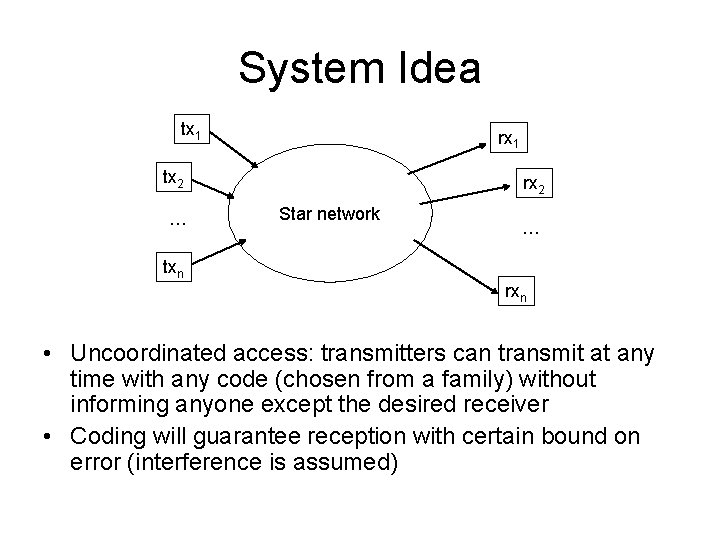
System Idea tx 1 rx 1 tx 2 … rx 2 Star network … txn rxn • Uncoordinated access: transmitters can transmit at any time with any code (chosen from a family) without informing anyone except the desired receiver • Coding will guarantee reception with certain bound on error (interference is assumed)

Design Parameters • Optical Channel: – 1 : light is transmitted – 0 : no light is transmitted • Channel Interference: Noncoherent interference is assumed – 1 : bit will always be correctly received – 0 : bit can be corrupted by interference • Channel rate: our goal is 2. 5 Gbps

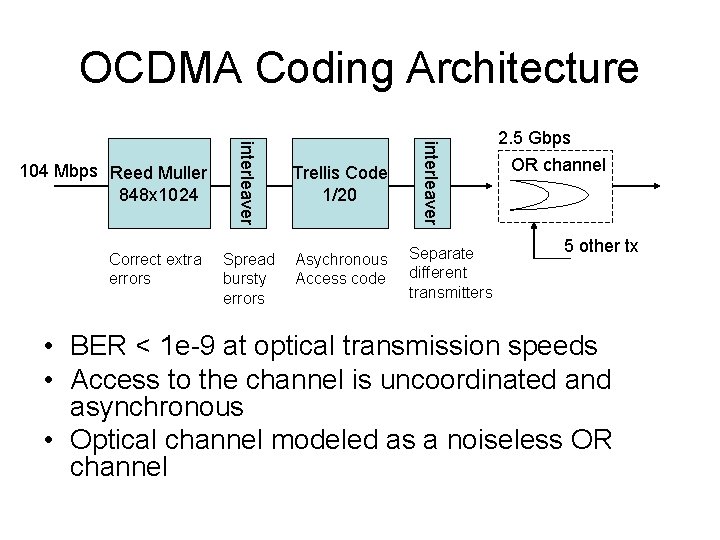
OCDMA Coding Architecture Spread bursty errors Trellis Code 1/20 Asychronous Access code interleaver Correct extra errors interleaver 104 Mbps Reed Muller 848 x 1024 Separate different transmitters 2. 5 Gbps OR channel 5 other tx • BER < 1 e-9 at optical transmission speeds • Access to the channel is uncoordinated and asynchronous • Optical channel modeled as a noiseless OR channel

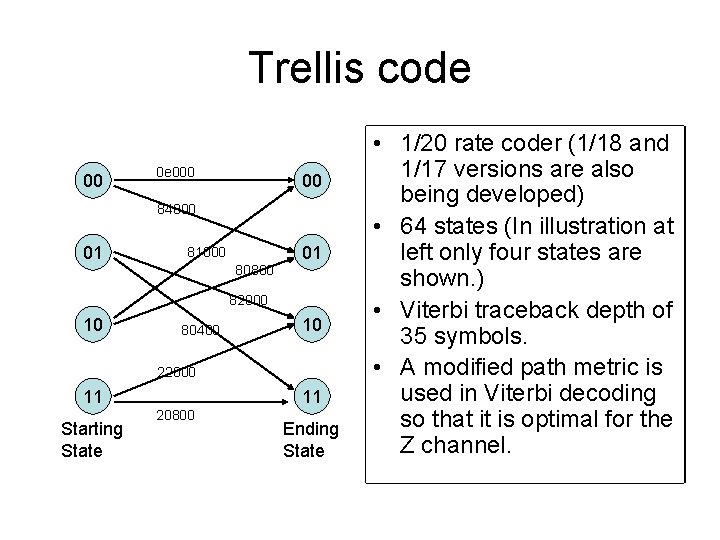
Trellis code 00 0 e 000 00 84000 01 01 81000 • 1/20 rate Data Txcoder (1/18 Newand versions are also bit 1/17 symbol state being developed) • 64 states (In illustration 1 84000 01 at 80800 82000 10 80400 10 Starting State 11 20800 0 • 22000 11 • Ending State 0 left only four states are shown. ) Viterbi traceback depth of 82000 10 35 symbols. A modified path metric is used in Viterbi decoding 00 for the so that it 81000 is optimal Z channel.

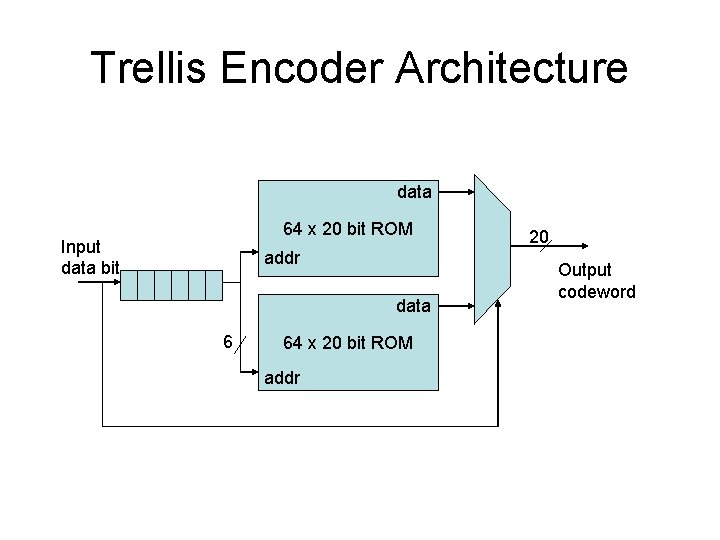
Trellis Encoder Architecture data 64 x 20 bit ROM Input data bit addr data 6 64 x 20 bit ROM addr 20 Output codeword

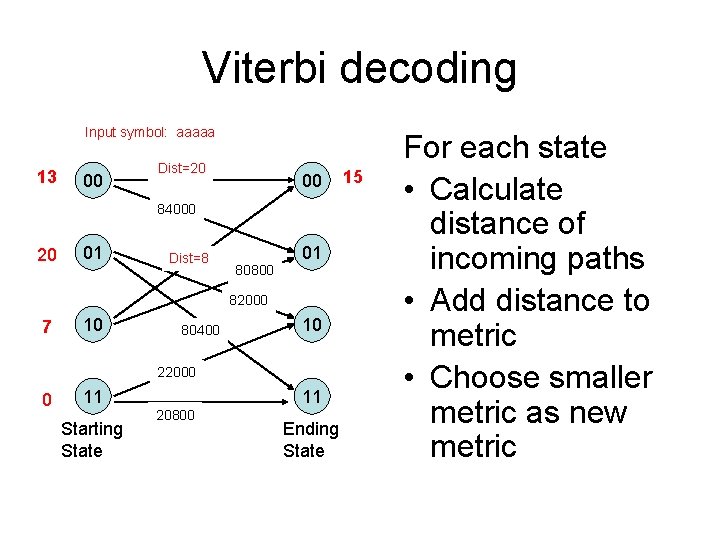
Viterbi decoding Input symbol: aaaaa 13 00 Dist=20 33 0 e 000 00 84000 20 01 82000 Dist=8 15 01 80800 82000 7 10 80400 10 22000 0 11 Starting State 11 20800 Ending State 15 For each state • Calculate distance of incoming paths • Add distance to metric • Choose smaller metric as new metric

Viterbi distance metric • In an OR channel it is impossible to receive bit 0 when a bit 1 is expected • When this situation is encountered the branch metric is automatically set to the maximum (20) Example: expected codeword 11100 Received codeword Path metric 01010 5 11100 0 11111 2

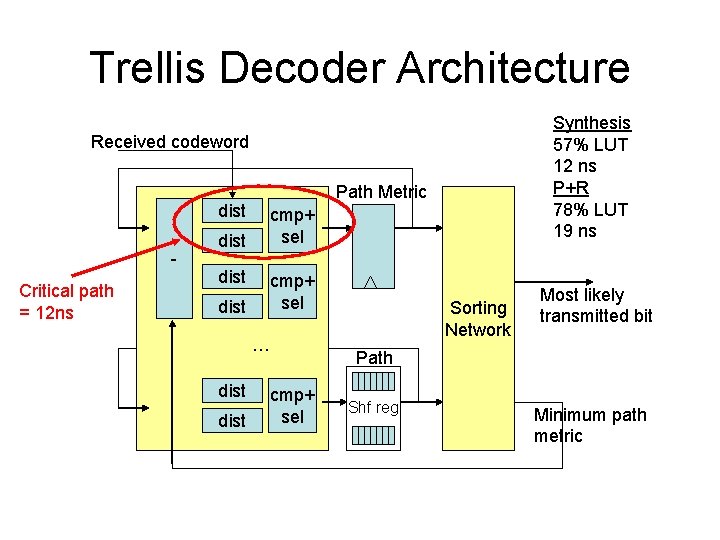
Trellis Decoder Architecture Synthesis 57% LUT 12 ns P+R 78% LUT 19 ns Received codeword Path Metric dist Critical path = 12 ns cmp+ sel dist … dist Sorting Network Most likely transmitted bit Path cmp+ sel Shf reg Minimum path metric

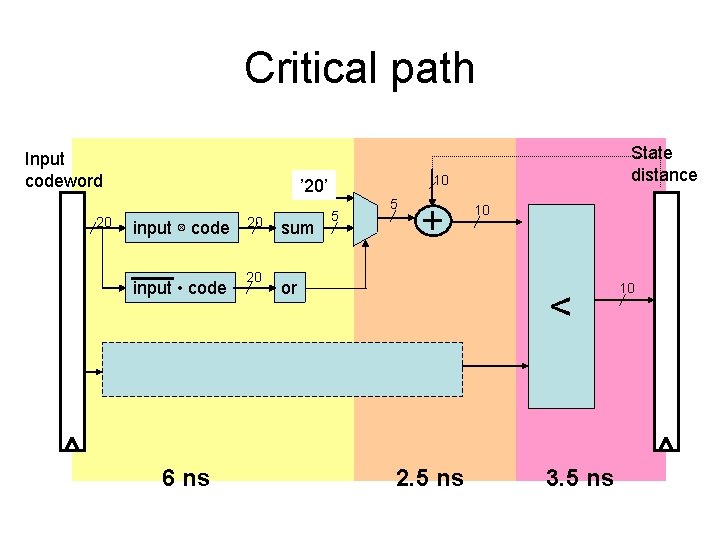
Critical path Input codeword 20 10 ’ 20’ input ⊗ code input • code 6 ns 20 20 sum State distance 5 5 or 10 < 2. 5 ns 3. 5 ns 10

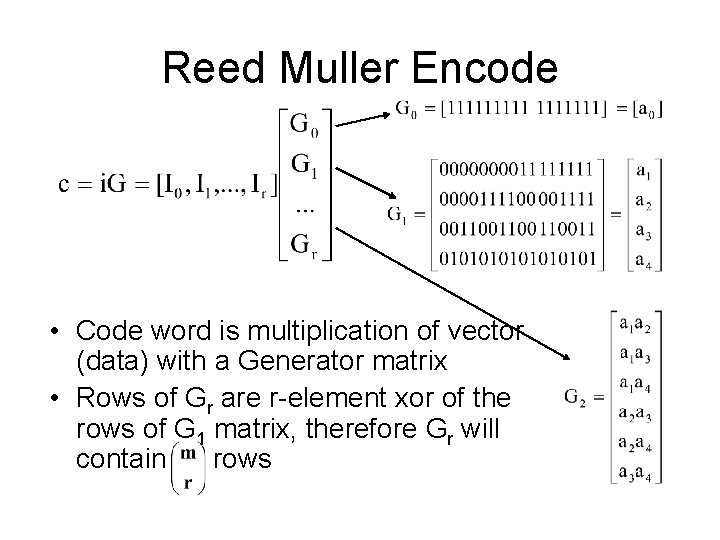
Reed Muller Encode • Code word is multiplication of vector (data) with a Generator matrix • Rows of Gr are r-element xor of the rows of G 1 matrix, therefore Gr will contain rows

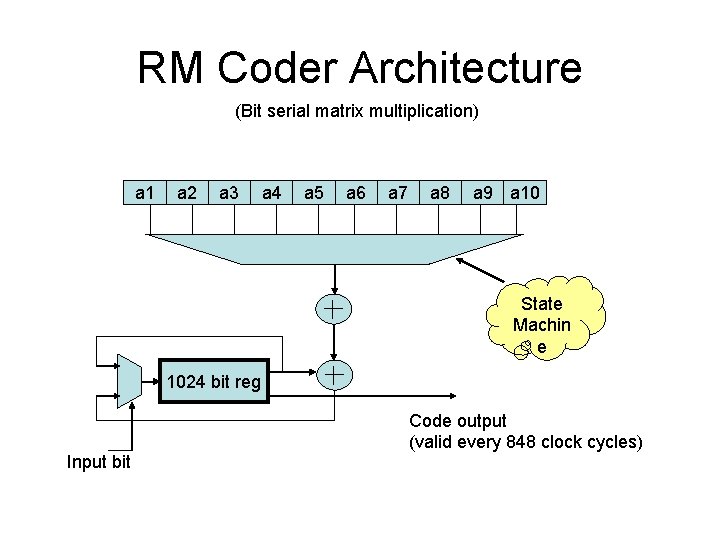
RM Coder Architecture (Bit serial matrix multiplication) a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 State Machin e 1024 bit reg Input bit Code output (valid every 848 clock cycles)

Reed Muller Decoding (r=1) • Each bit in is protected by 8 checksums • Calculate all 8 checksums; the majority of the results is the decoded bit

Reed Muller Code (r>1) • First decode information bits protected by submatrix Gr • Once level r has been decoded, subtract its contribution from the receive vector • The problem to solve is now reduced by one degree

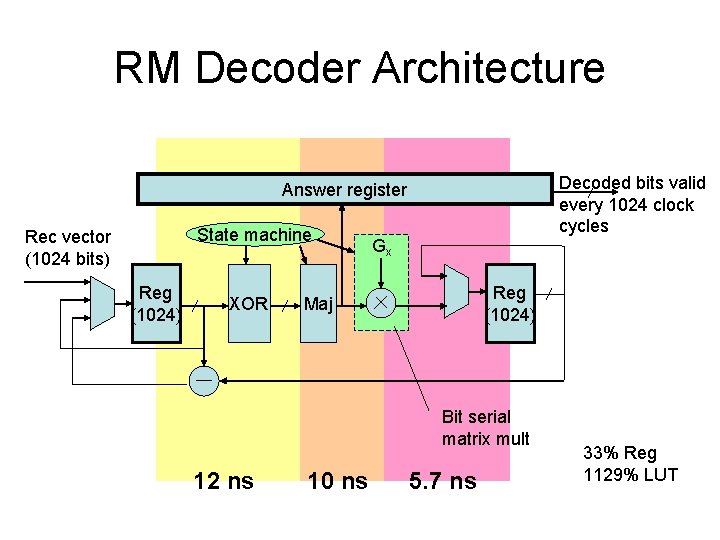
RM Decoder Architecture Decoded bits valid every 1024 clock cycles Answer register State machine Rec vector (1024 bits) Reg (1024) XOR Gx Reg (1024) Maj Bit serial matrix mult 12 ns 10 ns 5. 7 ns 33% Reg 1129% LUT

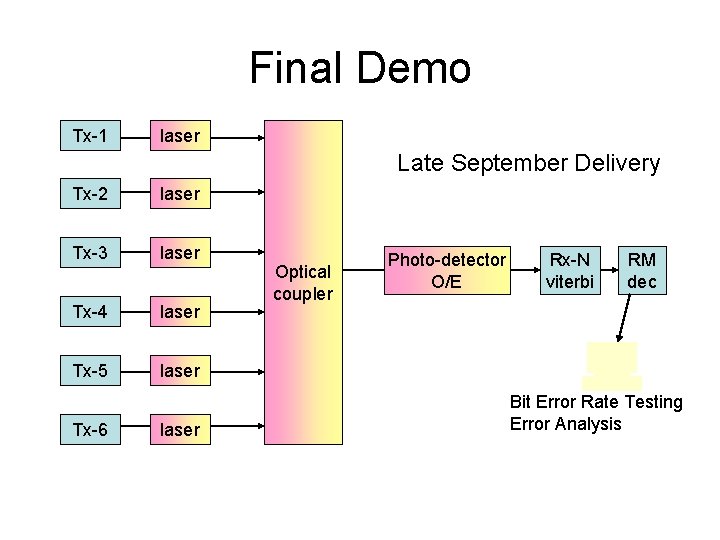
Final Demo Tx-1 laser Late September Delivery Tx-2 laser Tx-3 laser Tx-4 laser Tx-5 laser Tx-6 laser Optical coupler Photo-detector O/E Rx-N viterbi RM dec Bit Error Rate Testing Error Analysis